Arc Definition in Geometry

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

Circles and circumference

Circles are simple, but they do have parts. One part is an arc, a snippet of the circle, a piece of its circumference. Arcs themselves come in types, like major arcs, semicircles, and minor arcs.

A circle is the set of all points equidistant from a given point. Circumference is the distance around a circle.

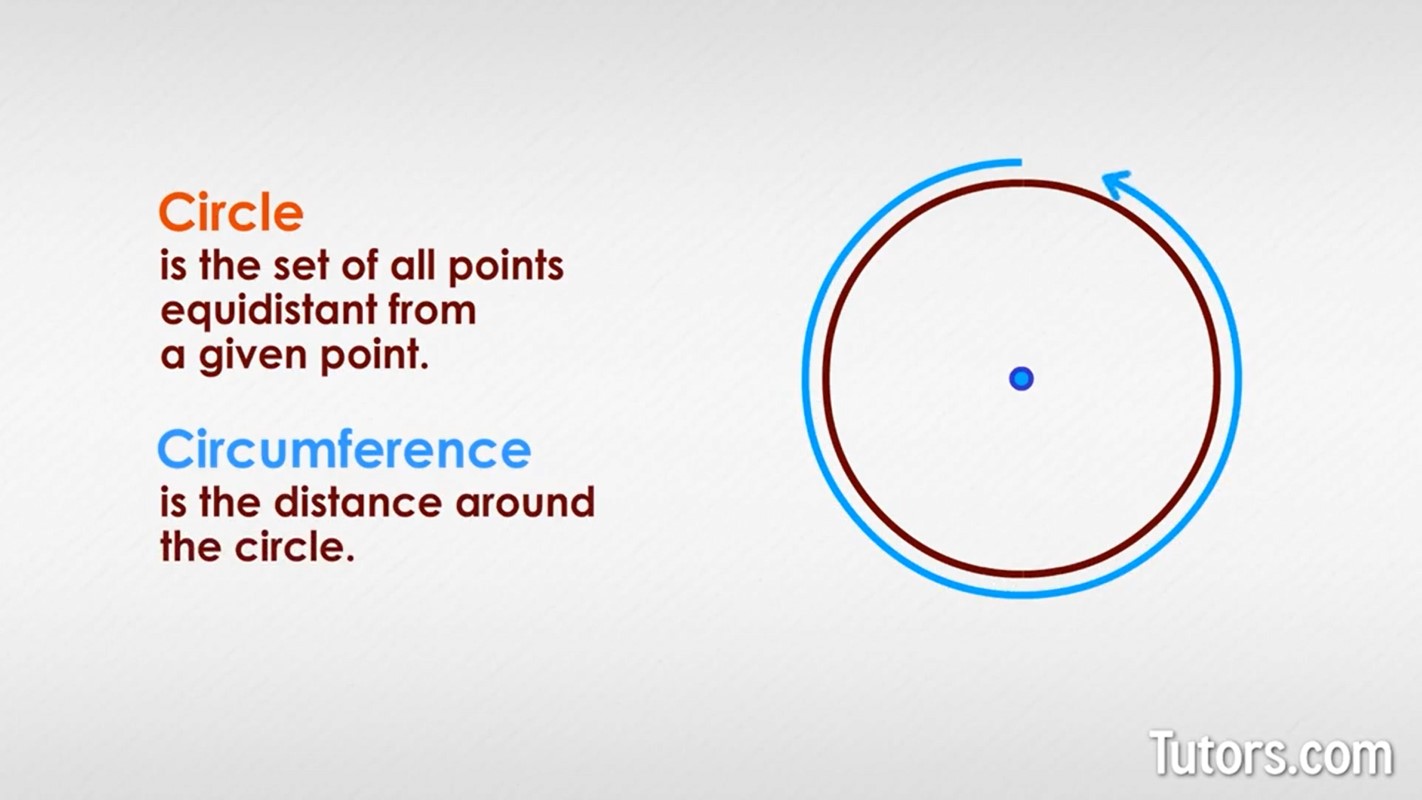
Circles can have angles created by two radii. These are central angles and are almost always designated using either their exact angle (or radian) measurement or the Greek letter theta, $\theta$.

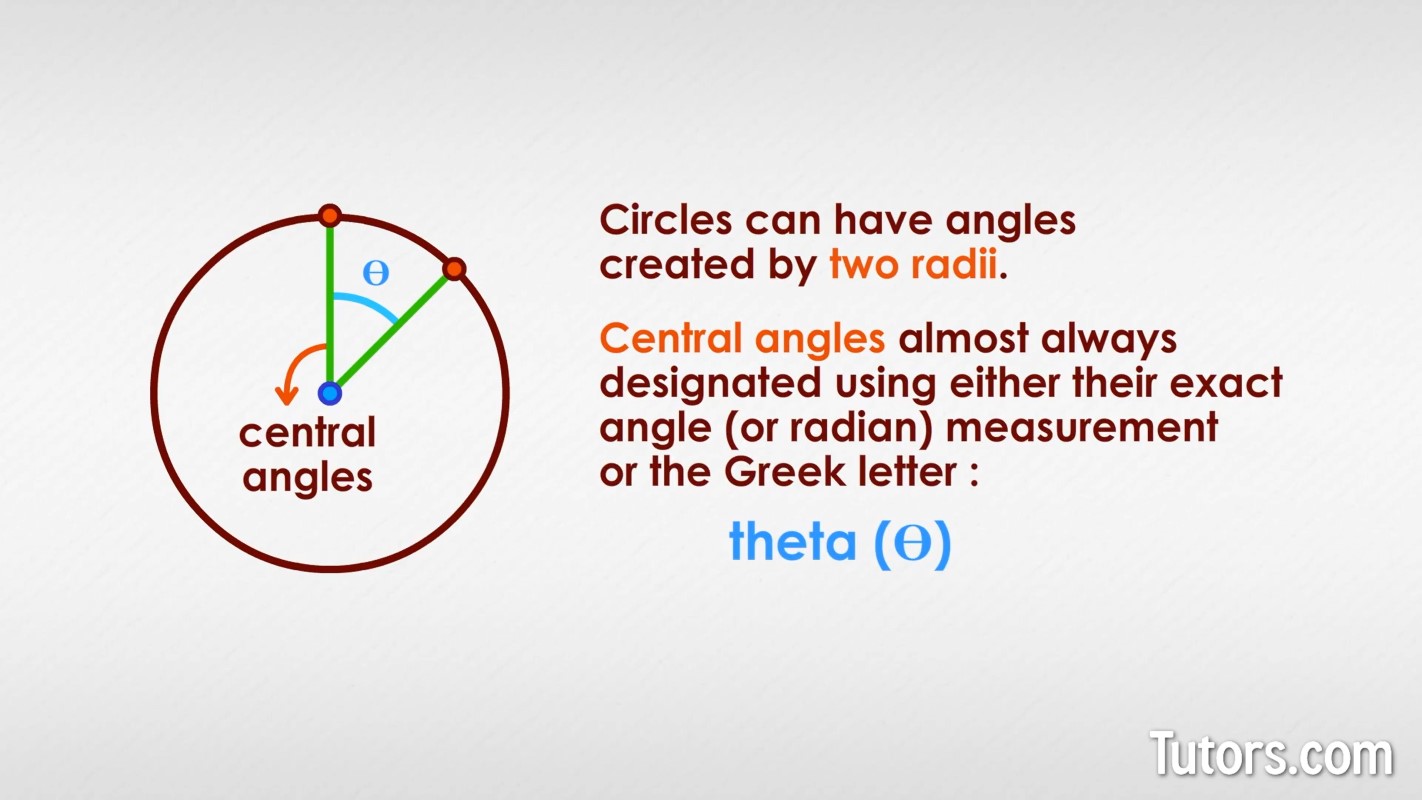
Circles can also have angles created by two chords (line segments with endpoints on the circle) with a common endpoint on the circle. These angles are called inscribed angles.

Both central angles and inscribed angles create major and minor arcs.

Semicircles and arcs

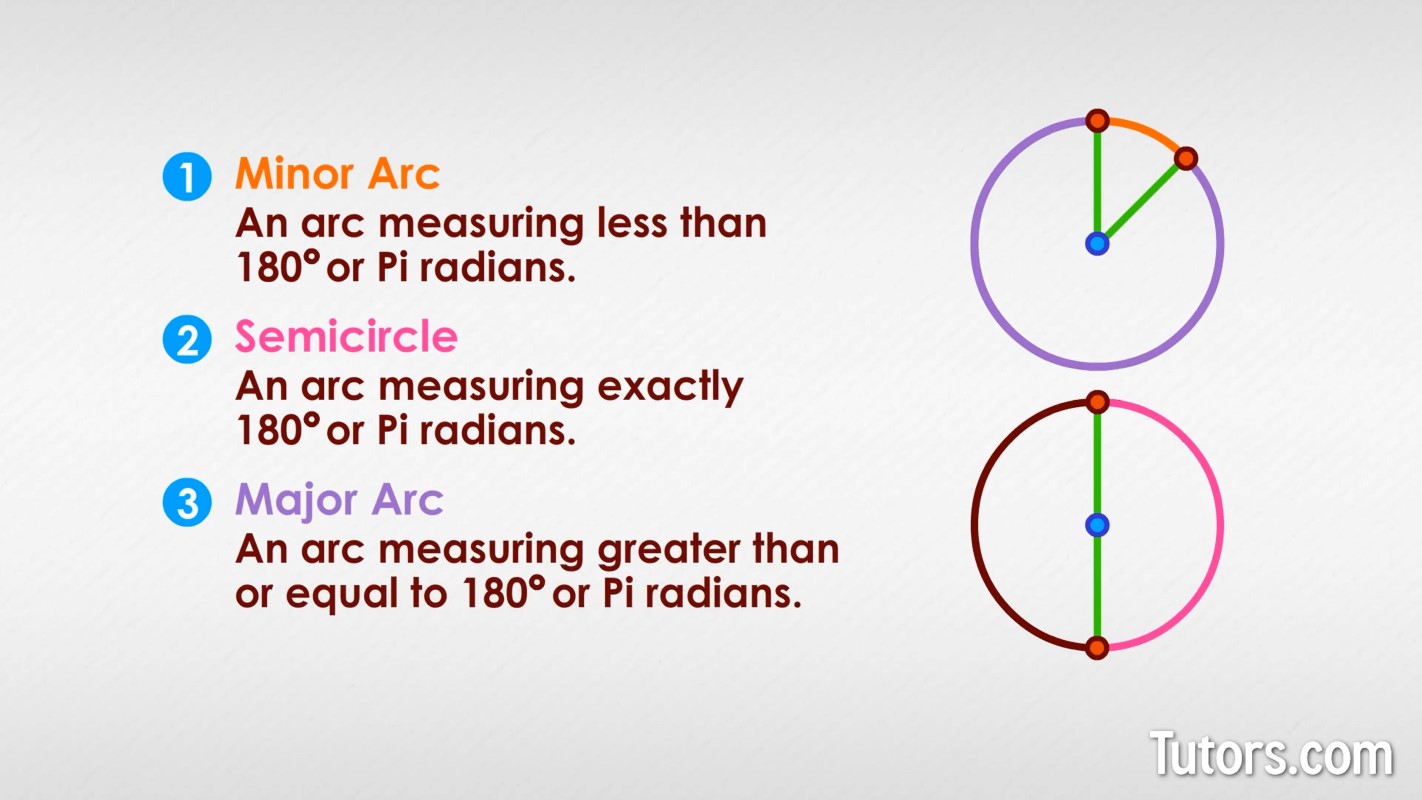
An arc is a portion of a circle that is less than the entire circle. Since that allows nearly all possible portions, mathematicians break down arcs like this:

1. Minor arc - An arc measuring less than or equal to 180° or $\pi$ radians

2. Semicircle - An arc measuring exactly 180° or $\pi$ radians, which excludes designating either part of the circle as major or minor

3. Major arc - An arc measuring greater than or equal to 180° or $\pi$ radians

Identifying arcs

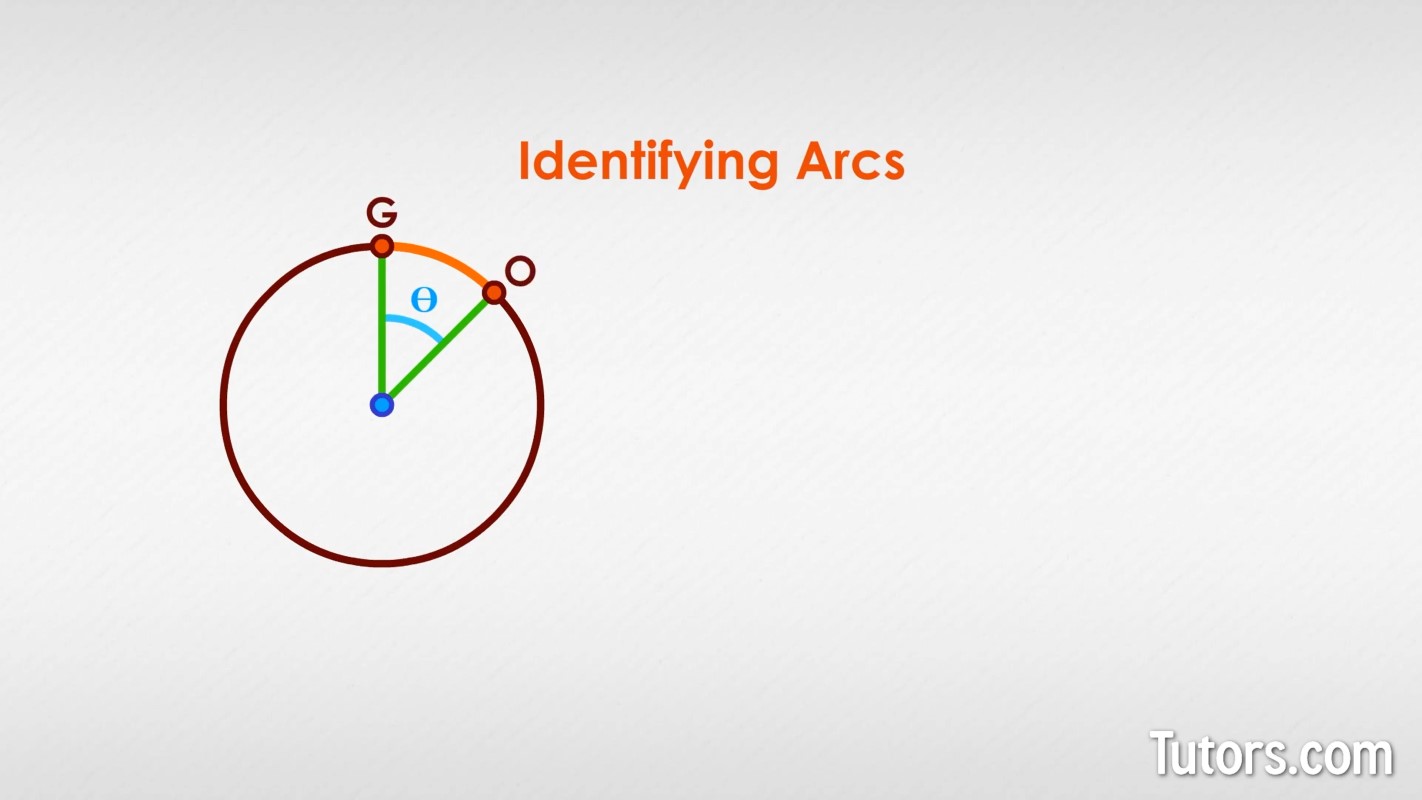
In a typical drawing of a circle, the reader understands the minor arc to be the one under discussion. In this drawing, we care about the minor arc identified by the central angle $\theta$.

Labeling a minor arc requires only its endpoints on the circle. Here is minor arc GO:

If you want the major arc, select and label both endpoints of the arc and a random point between. Here we have major arc FUN:

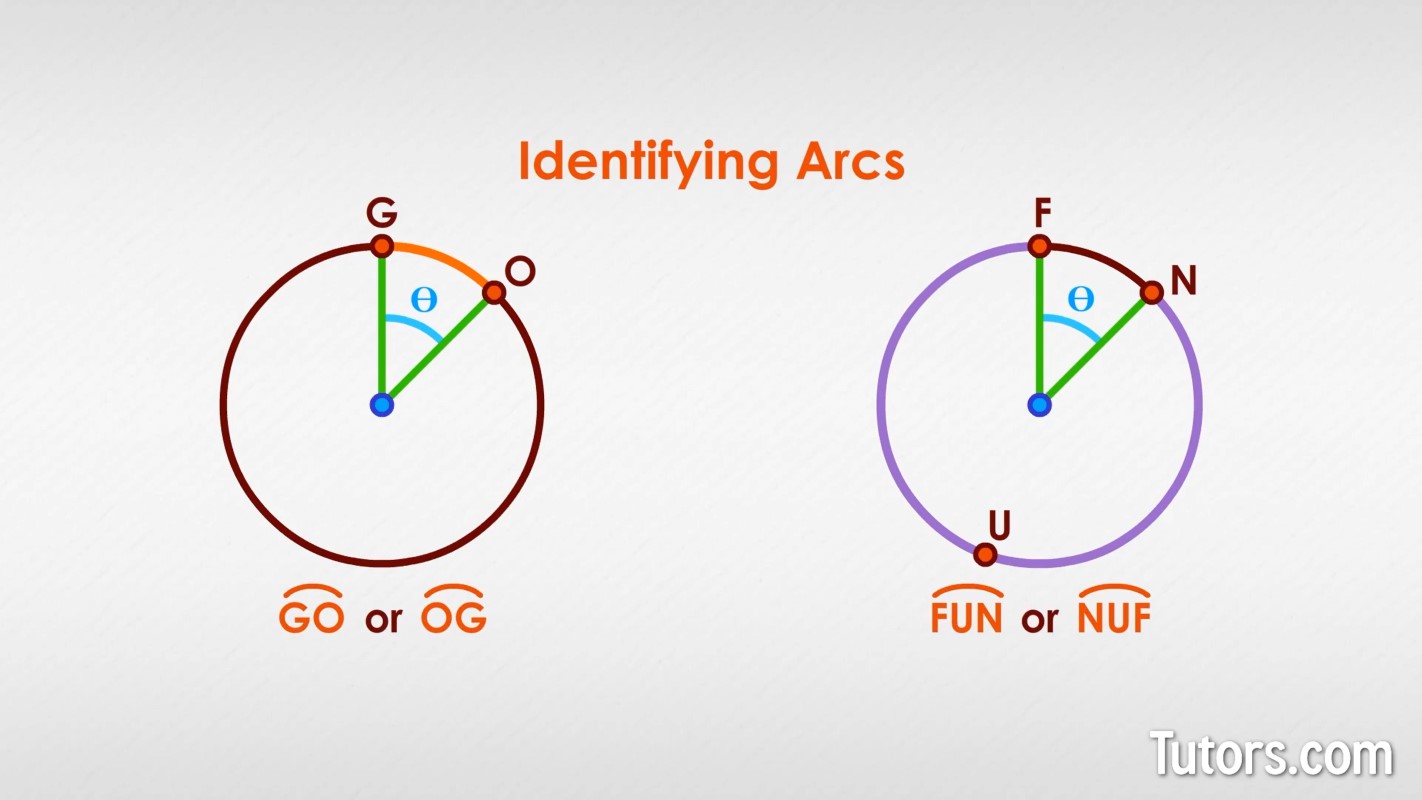
Arcs are usually identified in writing using their points (two for a minor arc, three for a major arc) and then drawing a tiny, short arc drawn over the letters.

Measuring arcs

Arcs have two measurements:

1. Angle

2. Length

One way to measure an arc is by the central angle of the circle. This is the arc angle. You place a lowercase m in front of the written form for the arc, like this:

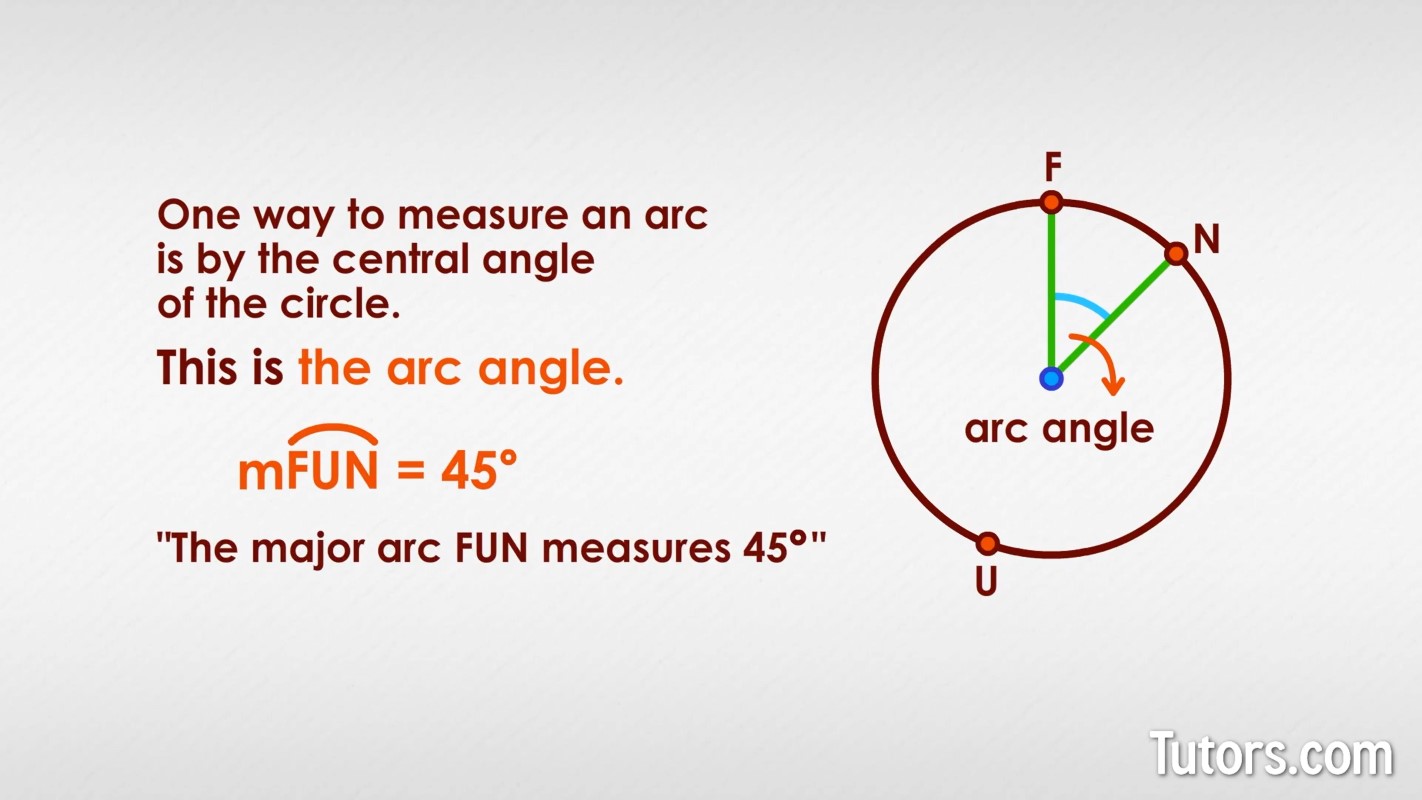
So you could write $m\overset\frown{FUN}=45°$, and you would say, "The major arc FUN measures 45 degrees."

The other way to measure arcs is by their distance along the circumference of the circle. This is the arc length. To write arc length in words, you put a small l in front of the written form, like this:

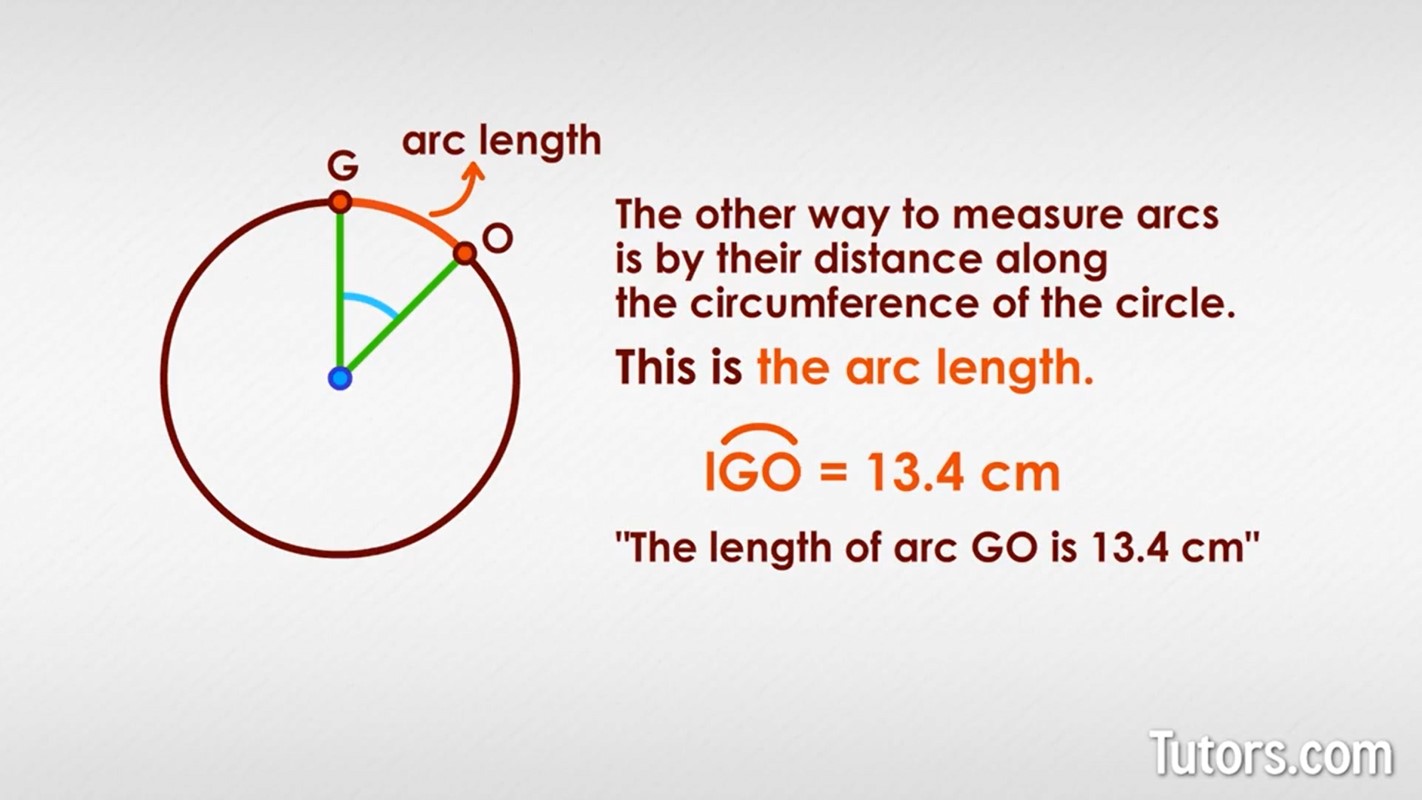
So you could write $l\overset\frown{GO}=13.4 cm$ and you would say, "The length of arc GO is 13.4 centimeters."