Angles of Elevation & Depression
Angle of depression
If you have ever watched a commercial airplane roll back from an airport gate, you may have noticed a crewmember on the ground giving signals to the pilot in the cockpit, many feet above.
Have you ever thought that the angle of sight for the ground crewmember is the same angle of sight for the pilot? The pilot's viewing angle is called the angle of depression, while the ground crewmember's viewing angle is the angle of elevation.
The Airbus A380 commercial airliner places the pilot's cockpit window an astounding 7.13 meters above the ground. From the height of a two-story building, the pilot looks down to the airport tarmac and must be able to see airport crewmembers giving visual signals.

If the pilot looks straight out, that line of sight is horizontal (focused on the distant horizon). The pilot might see the airport's runway, distant buildings, or even mountains in her field of view.
If the pilot looks down at the ground, she will see the ground crew. The angle of depression is the angle that is formed between the horizontal and the downward looking angle. It is always a downward view, an angle below the horizon.
Angle of elevation
For the ground crewmember, looking down would not be much help in communicating with the pilot in her cockpit seat. The crewmember will look up, above the horizontal line, to see the pilot. The ground crewmember's angle of vision if an angle of elevation, the angle above the horizon.
For both people's viewpoints -- the pilot's eyes in her cockpit seat 7.13 meters (around 23') above the tarmac, and the ground crewmember's eyes roughly 1.7 meters (about 5'-6") above the tarmac, both angles are the same. Look at this sketch:
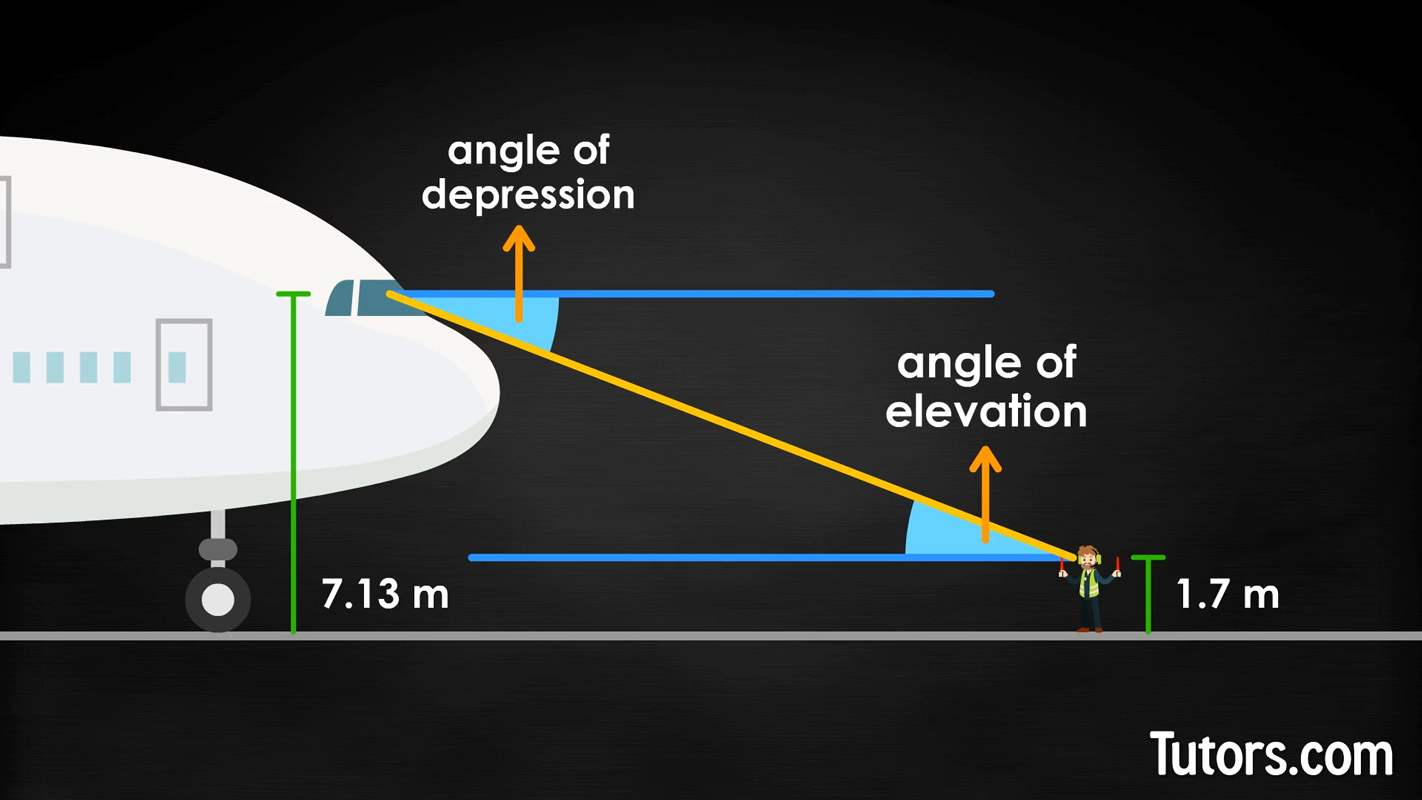
Notice the angle of depression is the same as the angle of elevation. Since the horizontal lines are parallel, this is a case of alternate interior angles created by a transversal (the line of sight) cutting across two parallel lines (the horizontals).
How to find the angle of elevation & depression
Animals and artists, pilots and pelicans all instinctively use the angle of depression. From a park ranger in a fire tower to that pilot taxiing or landing an A380 airliner, the angle of depression provides important information about distance and height.
Its opposite, the angle of elevation, is what humans do when they want to look up at tall mountains, nests in trees, or towering buildings.
Formulas for angle of elevation & depression
Recall the three trigonometric ratios (or identities), sine, cosine, and tangent. They each are the mathematical relationship between angles and sides and the hypotenuse of a right triangle:

If you know the tangent of an unknown angle (using the tangent formula), you can use the inverse of tangent, arctangent, to find the actual angle.
Finding the angles of elevation & depression
Let's look again at our pilot and ground crewmember. We can create a right triangle with the pilot at the top of the short side, the crewmember at the far end of the long side, and a hypotenuse (the line of sight) stretching between them. The long side is the ground crewmember's horizon line. The short side is the right angle straight up to the pilot.
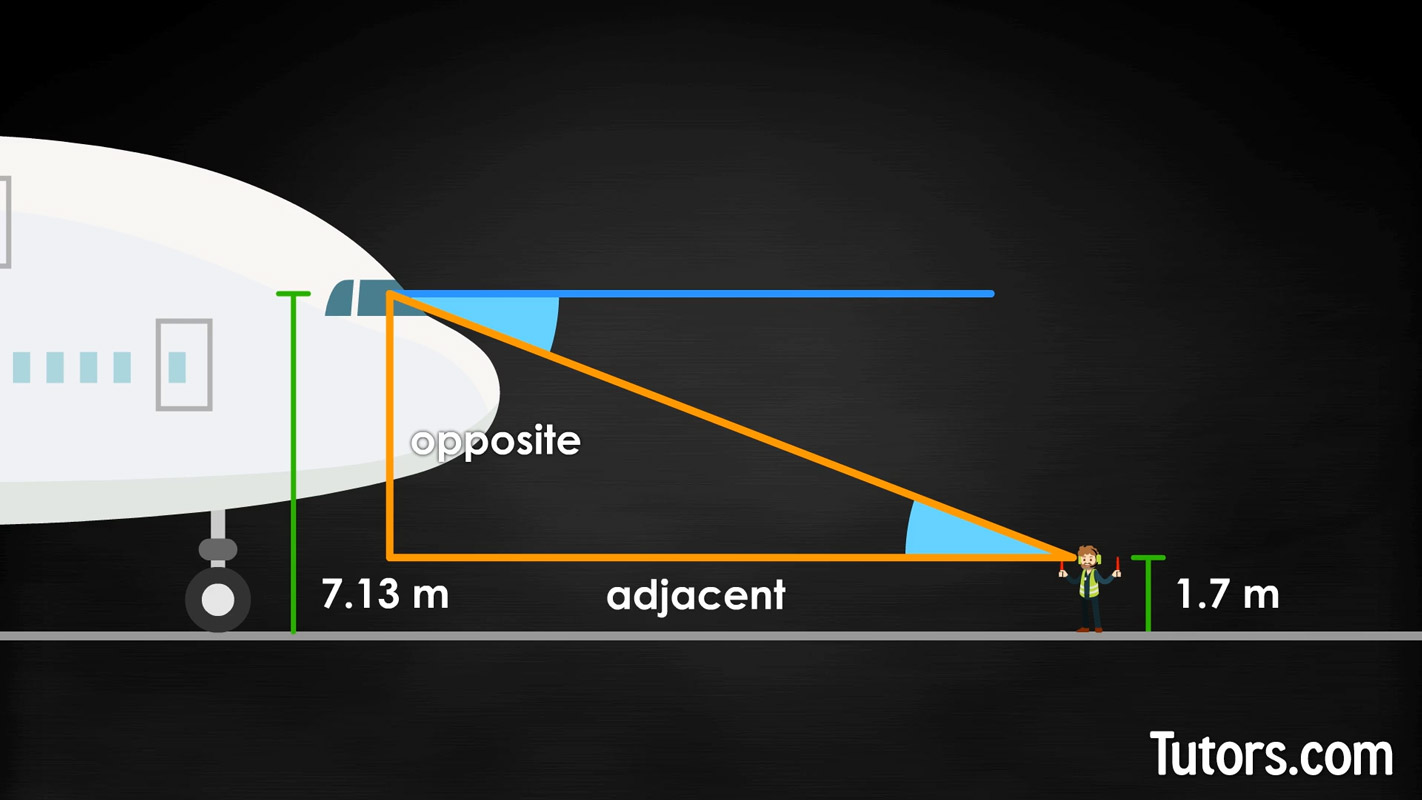
The height from the crewmember's horizon line to the pilot's eyes is our opposite side, and the adjacent side is the distance from that side to the ground crewmember. We know the height of the opposite side, from basic subtraction of the pilot's and the ground crewmember's eye positions above the tarmac:
The ground crewmember stands far enough away from the aircraft to see the pilot and be seen by her. Let's call that 25 meters, the length of the triangle's long side. We know the opposite side and adjacent side measurements, so we can find the tangent of the angle of depression for the pilot and angle of elevation for the crewmember (they are the same number, remember).
Setting up to find the tangent allows us to find the inverse, the angle itself, using arctangent:
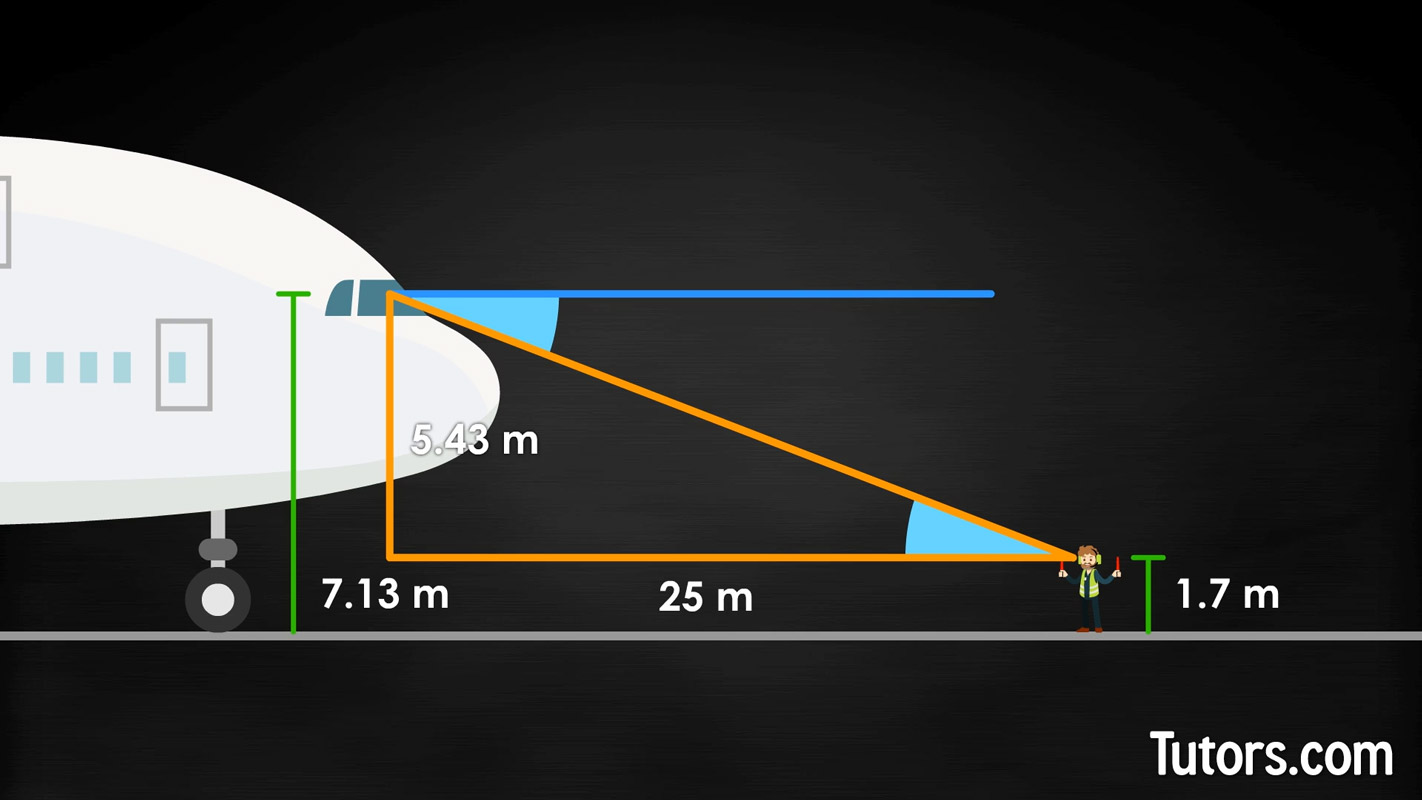
Opposite divided by adjacent:
Inverse of tangent to find the angle:
So the pilot is having to look down only 12.25° below horizontal, and the ground crewmember is looking up only 12.25° above horizontal, to see each other.
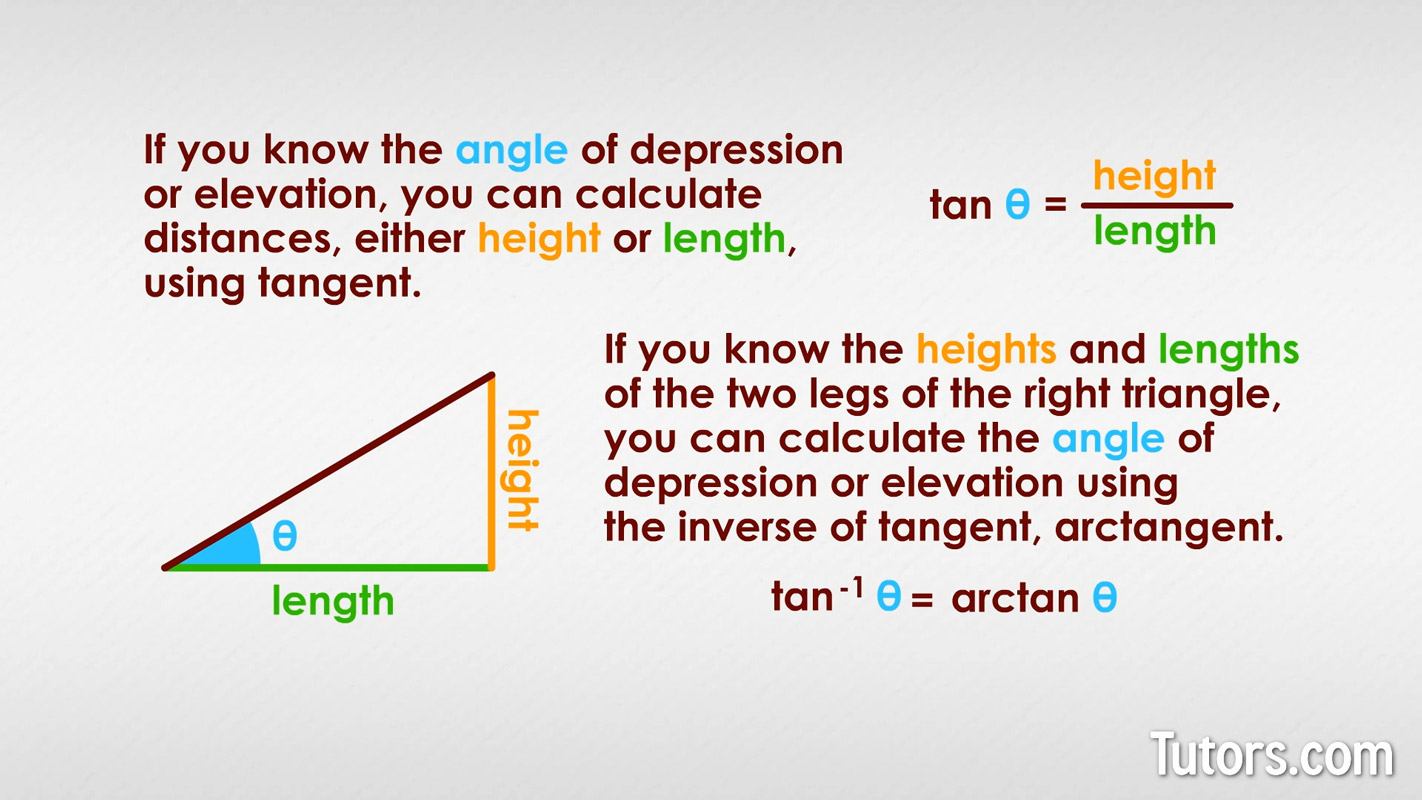
If you know the angle of depression (or elevation), you can calculate distances (either height or length) using tangent.
If you know the heights and lengths of the two legs of the right triangle, you can calculate the angle of depression (or elevation) using the inverse of tangent, arctangent.
Example problems
You dropped an egg on the kitchen floor. You are 1.5 meters above the floor, and 3.75 meters from the egg. To see the egg, what is your angle of depression?
You are looking down the Grand Canyon at an angle of depression of 45° and see a lovely rock formation on the canyon floor, which is one mile straight down. How far away from you is the rock formation?
So, the formation is one mile away from the canyon wall.
Lesson summary
Now that you have studied this lesson, you are able to recall and define angle of depression and angle of elevation, relate the angle of depression to the angle of elevation, cite examples from everyday life of the angle of depression and the angle of elevation, and use tangent and arctangent to calculate an angle of depression or an angle of elevation.