How to Find the Area of a Pentagon (Formula & Example)
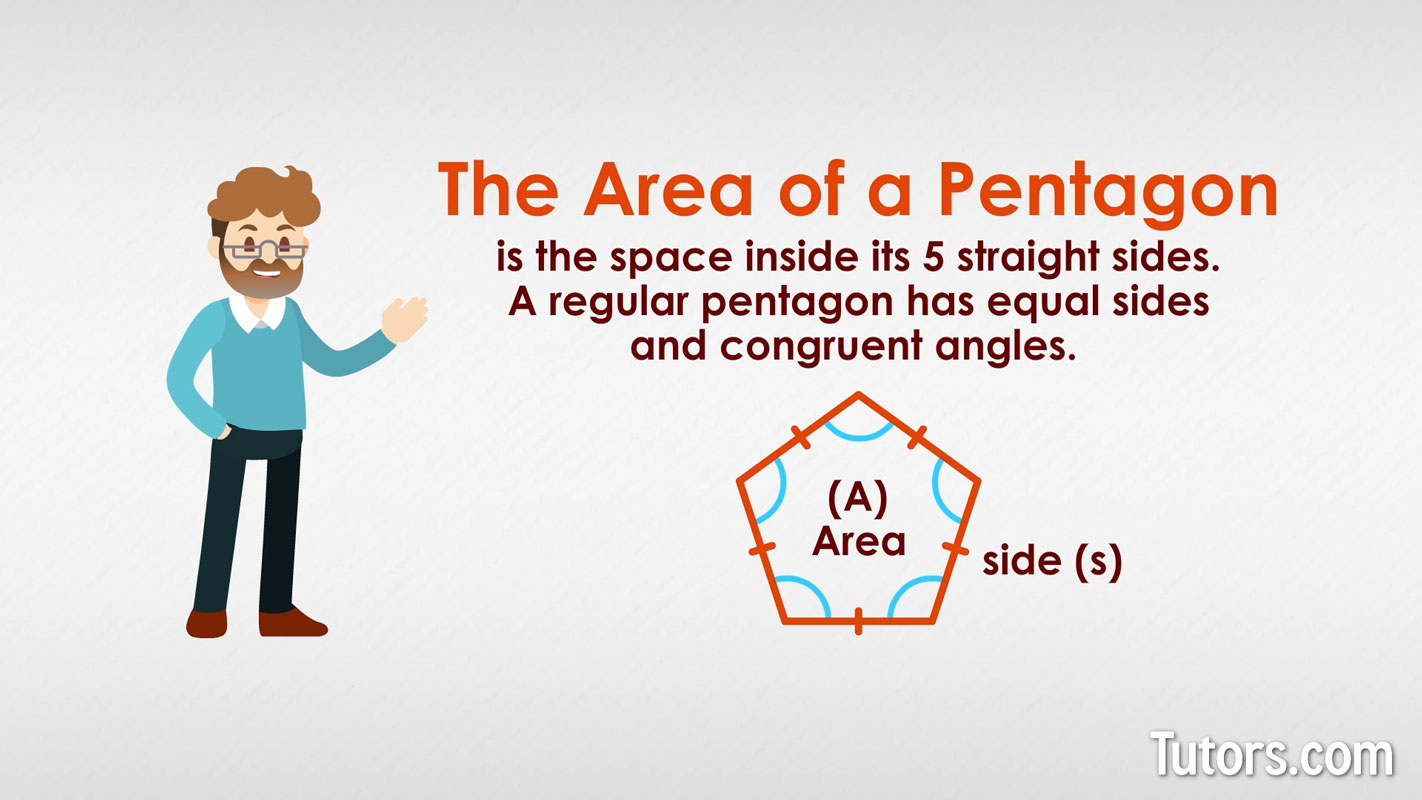
Area of a pentagon
The area of a pentagon is the space inside its five straight sides. Most of the time, you will be tasked with finding the area of a regular pentagon, so this lesson will not cover irregular pentagons.
A regular pentagon has equal sides and congruent angles. There are a couple of methods you can use to calculate the area of a regular pentagon. One method uses a side length and length of the apothem.
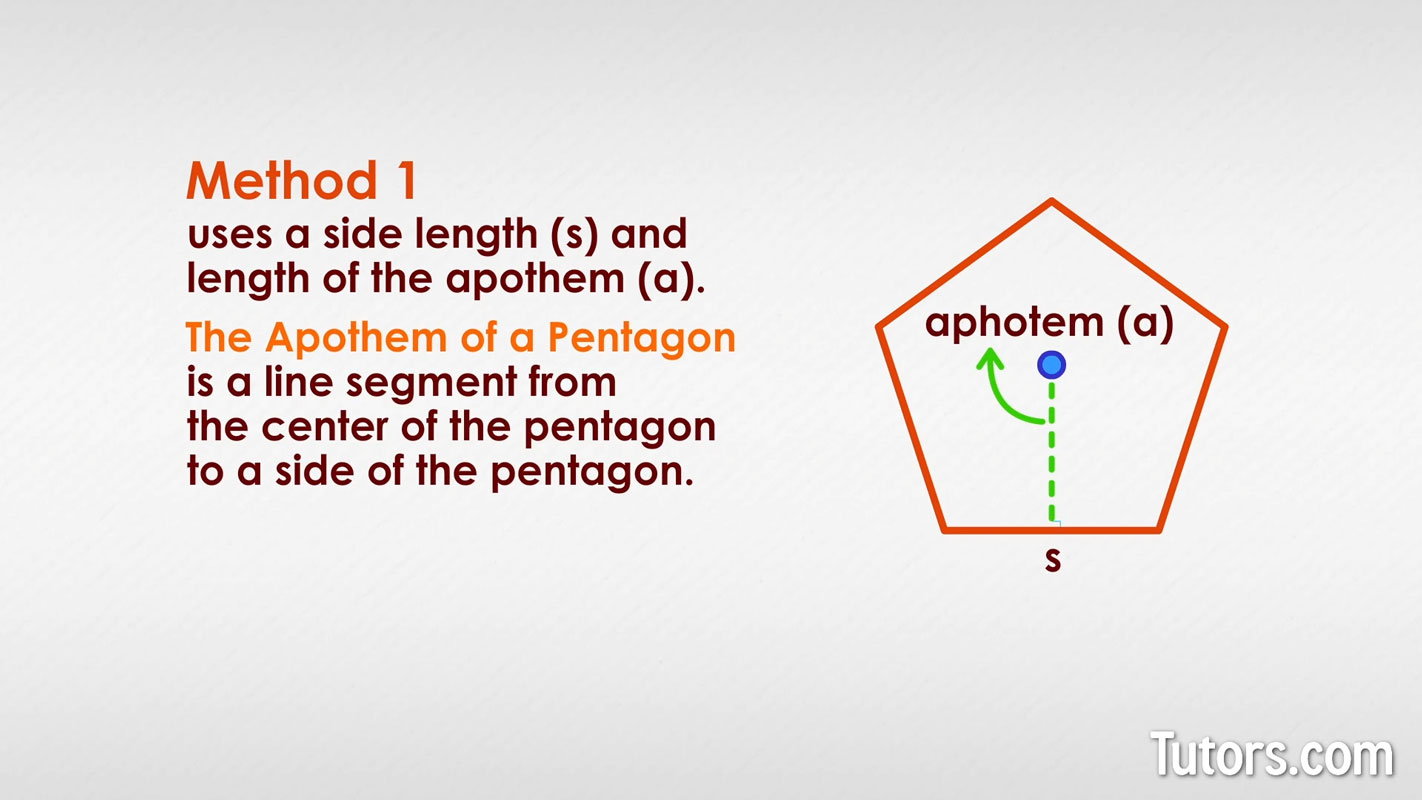
Apothem of a pentagon
The apothem of a pentagon is a line segment from the center of the pentagon to a side of the pentagon. The apothem is perpendicular to the side. All regular polygons have an apothem. For a polygon of n sides, there are n apothems.
Area of a pentagon formula
To find the area of a pentagon with the apothem, a, and one side length, s, you use the area of a pentagon formula:
What if you do not know the apothem of your pentagon? You can still find the area of a regular pentagon if you know:
A little trigonometry
The length of one side
Each interior angle measures 108°
You know that each interior angle measures 108° because you know a few things about exterior angles and polygons. You know that:
The sum of the exterior angles of any polygon add up to 360°
The exterior angle is the supplement of the interior angle (interior + exterior = 180°)
To find the measure of each exterior of a regular polygon, you divide 360° by the number of sides. For a pentagon that is . This tells us each exterior angle is 72°.
Now we can use that to determine the measure of each interior angle. Remember, the exterior angle and interior angle must add to 180°, so we have 180° − 72° = 108°. Each interior angle equals 108°.
How to find the apothem and area of a pentagon
Using the length of one side and the measure of the interior angle, let's calculate the apothem length and find the area of a regular pentagon.
Let's say we have a pentagon with a side length of 4 cm. Divide the pentagon into five isosceles triangles, each with a base formed by the pentagon's sides. Now, divide any one of those triangles into two right triangles: You now know all this about the right triangle:
The length of the triangle’s short leg ( the pentagon’s side)
The right angle (90° angle) is opposite the hypotenuse (perpendicular bisector of the side)
36° acute angle opposite the short leg 360° divided among 10 right triangles)
54° acute angle opposite the long leg ( of the 108° interior angle)
The tangent of an angle (here, our 36° angle) is the opposite side (the short leg) divided by adjacent side (the long leg, which is both the height of the triangle and the apothem of the pentagon):
The tan(36°) is approximately 0.727, so we have the opposite side (the short leg) of 2 cm divided by 0.727:
With the height, h, of the triangle now established and knowing the triangle’s base (; the pentagon’s side), b, you can now apply the formula for the area of a triangle:
We have 10 such right triangles, so we modify the triangle area formula and calculate the area of our regular pentagon:
The one half and the ten can be combined:
Now, we plug in the numbers that we know for the base and height:
And we arrive at our answer:
The total area of the pentagon is . Area is always expressed in units squared or square units.