20+ tutors near you & online ready to help.

TABLE OF CONTENTS

Geometric Probability

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

What is probability?

Probability is the likelihood of a desired outcome against all possible outcomes.

An archery target for recreational target practice is often just a large circle with four other circles inside it. As you get closer to the center, the points you win increase: 1, 3, 5, 7, and 9 for the bullseye. You can use geometric probability to calculate the chance of hitting a bullseye.

If something can never happen, its probability is 0, which could also be considered 0 percent.
If something may or may not happen, its probability is between 0 and 1, or from 0 percent to 100 percent.
If something is absolutely certain to happen, its probability is 1, or 100 percent.

The desired outcome of an event, like the roll of two dice, is the probability you want; subtracted from 1, it leaves the probability of unfavorable outcomes.

Together, what you want to have happen and everything that could happen will add to 1, or to 100 percent.

We can illustrate this with dice:

[insert three pictures of sets of normal dice, or possibly make a video showing the three probabilities?]

The probability of getting a total of 1 from two, six-sided, normally marked dice is 0, or 0 percent.
The probability of getting a 7 from two, six-sided, normally marked dice is 0.166666667, or 16.66 percent.
The probability of getting a number ranging from 2 to 12 from two, six-sided, normally marked dice is 1, or 100 percent.

Get free estimates from geometry tutors near you.

Geometric probability

Here is a square with a smaller square inside it, tucked in the corner:

[insert drawing of square, like a tic-tac-toe board, with one corner staked out as a smaller, shaded square; smaller square is 1/9 of the larger one]

We got the little square by dividing height and width into three equal sections, so the little square is one square out of nine squares. Geometric probability is the chance of hitting the little shaded square, say with a dart or arrow, out of hitting anywhere on the square.

The shaded square is $\frac{1}{9}$ of the whole area, so the probability of hitting it is $\frac{1}{9}$ , while the chance of not hitting it is $\frac{8}{9}$ . Together, these two probabilities add to $\frac{9}{9}$ , or 100%. To find the geometric probability of an event, we use this formula, where P is the probability:

P=\frac{desired}{total}

Imagine the big square is 9 cm wide and 9 cm tall. That makes the little square 3 cm × 3 cm, or $9c{m}^{2}$ . The large square is $81c{m}^{2}$ , so the geometric probability of hitting the little square is:

P=\frac{9c{m}^{2}}{81c{m}^{2}}

P=\frac{1}{9}

As a decimal, $\frac{1}{9}$ is (interestingly, we think) 0.111111, which is far closer to 0 than to 1. If you were given a small beanbag and invited to toss the beanbag onto the big square, you do not have a very good chance of hitting the little shaded square.

Geometric probability of Greenland's flag

The flag of Greenland is interesting, both for its meaning (white is snow and ice; red is the sun) and its mathematics.

And here is a diagram showing its proportions:

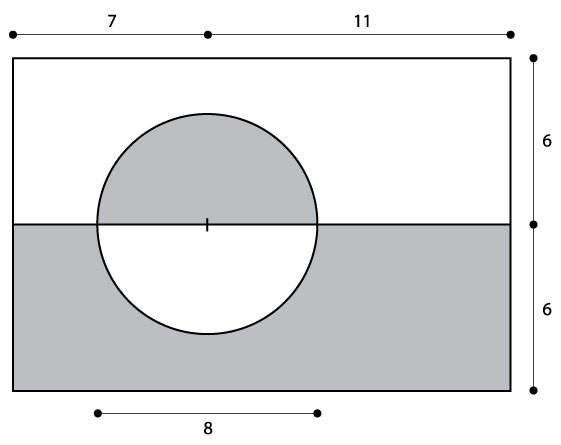
We can see that the entire flag is 18 units wide x 12 units tall. It is designed in abstract units so you could make it in cm, m, inches, or feet, so long as you kept all the ratios and proportions the same.

To see if you get the hang of geometric probability, try these three questions:

What is the total area of Greenland's flag?

The flag is 18 × 12 units, for an area of $216unit{s}^{2}$ .

The circle is 8 units in diameter (4 units in radius). If the area of a circle is $\pi {r}^{2}$ , what is the circle's area?

The circle's area is calculated by $A=\pi {r}^{2}$ .

A=\pi \cdot {4}^{2}

A\approx 50.265unit{s}^{2}

What is the geometric probability of a Greenland butterfly, the Arctic fritillary, accidentally flying into the circle?

P=\frac{50.265unit{s}^{2}}{216unit{s}^{2}}

P=0.23270

P=23.27%

P = 23.27%, or less than a 1-in-4 chance.

Let's make it more interesting. Notice that half of the circle is white, and half is red. What is the geometric probability that the butterfly will bump into only the red part of the circle?

You already know the geometric probability of hitting the circle: 0.23270, so since the red part is half of the circle, that makes the red area half of the whole circle, or 0.11635, which is around 11.63 percent.

Ready to try one more?

What is the geometric probability that our little Greenland butterfly will bump into any red area of Greenland's flag? If you look carefully, the half-circle of red could flip downward, to make the entire bottom half of the flag all read. So:

P=\frac{{\left(18\times 6\right)}^{2}}{{\left(18\times 12\right)}^{2}}

P=\frac{{108}^{2}}{{216}^{2}}

P=0.5

P = 0.5 or a 50% chance So now, if you ever go to Greenland, you will not only know the flag, you will know the geometric probability of its elegant, simple design.

Geometric probability of a bullseye

Suppose you have an archery target that is a circle 60 cm in diameter, with a bullseye 5 cm in diameter. What is the geometric probability of hitting the bullseye? Let's start with our formula for the area of a circle for the archery target:

A=\pi {r}^{2}

A=\pi \cdot {30}^{2}

A=\pi \cdot 900

A\approx 2827.43339c{m}^{2}

Now, let's take a look at the bullseye:

A=\pi \cdot 5c{m}^{2}

A=\pi \cdot 25

A\approx 78.53982c{m}^{2}

Now we can calculate the geometric probability:

P=\frac{78.53982c{m}^{2}}{2827.43339c{m}^{2}}

P=0.02777777905

P=2.7%

Get free estimates from geometry tutors near you.

You need real skill to hit a bullseye, because you only have a 2.7% chance of doing it at random!

Lesson summary

Now that you have explored this lesson (and a little geography), you are able to explain the concept of probability ranging from 0 to 1, recall and state a definition of geometric probability, and use the formula for geometric probability to calculate the likelihood of an outcome involving flat shapes.