Distributive Property — Definition, Uses & Examples
Distributive property definition
In math, distributive property says that the sum of two or more addends multiplied by a number gives you the same answer as distributing the multiplier, multiplying each addend separately, and adding the products together.
| PEMDAS Order of Operations | Using Distributive Property |
|---|---|
| (5 + 7 + 3) x 4 | (5 + 7 + 3) x 4 |
| = 15 x 4 | = (5 x 4) + (7 x 4) + (3 x 4) |
| = 60 | = 20 + 78 +12 |
| = 60 |

What is distributive property?
Distributive property is one of the most used properties in mathematics. It is used to simplify and solve multiplication equations by distributing the multiplier to each number in the parentheses and then adding those products together to get your answer.
| Step | |
| 7 x (7 + 5 + 8) = ? | Given equation |
| 7(7) + 7(5) + 7(8) = ? | Distribute the multiplier |
| 49 + 35 + 56 = ? | Multiply |
| = 140 | Add |

Distributive property connects three basic mathematic operations in two pairings:
multiplication and addition
multiplication and subtraction
The Distributive Property states that, for real numbers a, b, and c, two conditions are always true:
a(b + c) = ab + ac
a(b - c) = ab - ac
You can use distributive property to turn one complex multiplication equation into two simpler multiplication problems, then add or subtract the two answers as required.
Distributive property of multiplication
The distributive property is the same as the distributive property of multiplication, and it can be used over addition or subtraction.
Here are examples of the distributive property of multiplication at work:
| Distributive Property Over Addition | Distributive Property Over Subtraction |
|---|---|
| 6 x (10 + 5) | 6 x (10 + 5) |
| = (6 x 10) + (6 x 5) | = (6 x 10) - (6 x 5) |
| = 60 + 30 | = 60 - 30 |
| = 90 | = 30 |
Distributive property of division
The distributive property does not apply to division in the same sense as it does with multiplication, but the idea of distributing or “breaking apart” can be used in division.
The distributive law of division can be used to simplify division problems by breaking apart or distributing the numerator into smaller amounts to make the division problems easier to solve.
Instead of trying to solve , you can use the distributive law of division to simplify the numerator and turn this one problem into three smaller, easier division problems that you can solve much easier.

Distributive property examples
These example problems that may help you to understand the power of the Distributive Property:
11 x (10 + 5) = ?
11(10) + 11(5) = ?
110 + 55 = 165
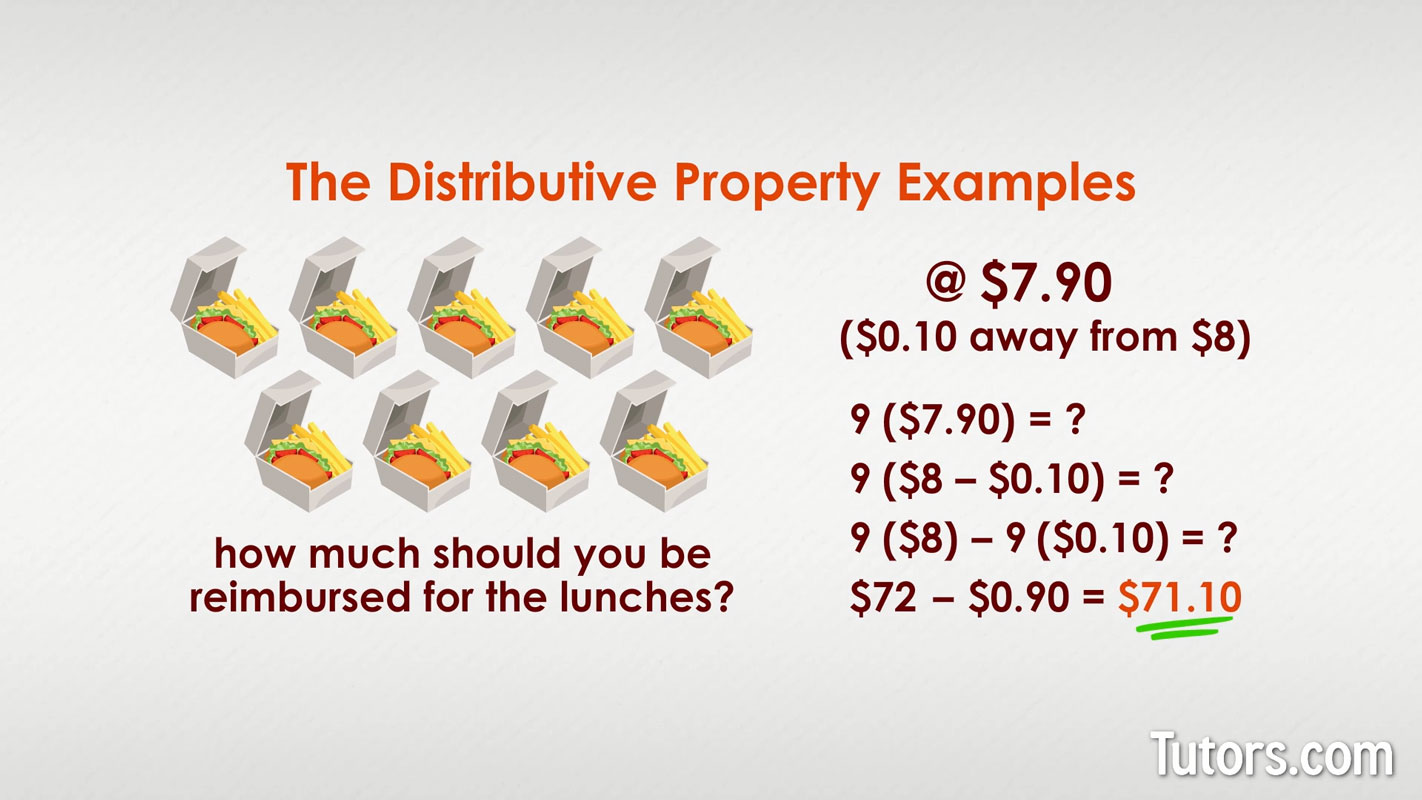
Too easy? Let’s try a real-life word problem using money amounts: You buy nine boxed lunches for the members of Math Club at $7.90 each. Using mental math, how much should you be reimbursed for the lunches? You notice that $7.90 is only $0.10 away from $8, so you use the Distributive Property:
9($7.90) = ?
9($8 - $0.10) = ?
9($8) - 9($0.10) = ?
$72 - $0.90 = $71.10
The Math Club treasurer should reimburse you $71.10 for the lunches.
How to use distributive property?
In basic operations, the Distributive Property applies to multiplication of the multiplicand to all terms inside parentheses. This is true whether you add or subtract terms:
The Distributive Property allows you to distribute the multiplicands or factors outside the parentheses (in this case, 2 and −6), to each term inside the parentheses:
You can use the characteristics of the Distributive Property to “break apart” something that is too hard to do as mental math, too:
Expand the multiplier and distribute the multiplicand to each place value:
Associate (group) addends for easier mental addition:
Distributive property algebra
In algebra, the Distributive Property is used to help you simplify algebraic expressions, combine like terms, and find the value of variables. This works with monomials and when multiplying two binomials:
Distribute the 3 and the −1:
Combine like terms:
Subtract 28 from both sides:
Divide both sides by 14:
Here is another more example of how to use the distributive property to simplify an algebraic expression:
Use the distributive property:
Simplify:
Combine like terms:

You may be familiar with the steps to solving binomials as the FOIL method:
First terms of each binomial are multiplied
Outer terms — the first term of the first binomial and the second term of the second binomial are multiplied
Inner terms — the second term of the first binomial and the first term of the second binomial are multiplied
Last terms — the last terms of each binomial are multiplied
Negative and positive signs with the distributive property
Distributive Property works with all real numbers, which includes positive and negative integers. In algebra especially, you need to pay careful attention to negative signs in expressions.
Review the steps above we used in this problem, above:
We added a + sign after the first term and distributed a −1 to a and 8, like this:
We then distributed the negative sign to both terms within the second parentheses:
We can show this distribution of the negative sign with two generic formulas, one for addition and one for subtraction:
-(a + b) = -a - b
-(a - b) = -a + b
Distributive property in geometry
We can apply the Distributive Property to geometry when working with problems involving the area of rectangles. Though algebra may seem unrelated to geometry, the two fields are strongly connected.
Suppose we are presented with a drawing that lacks numbers but does show a relationship.
We have no idea what the width and length are, but we are told that the rectangle has an area of 65 square meters. How do we calculate width and length?
We know that area is width times length (w x l) which in this case is x for the width and x + 8 for the length, or (x)(x+8).
Write down what we know:
Distribute x:
Convert it to a quadratic equation (subtract to make one side equal to 0):
Factor the quadratic equation:
We cannot have a negative number for width or length, so the correct answer is that x, the width, is equal to 5. This means the length, x+8, is equal to 13. We can check our work:
