Distance Formula
Distance formula calculator
How it works: Type the two x coordinates and two y coordinates into the boxes below and it will automatically calculate the distance between those 2 points and show you step by step.
Distance between two points
In a Cartesian grid, to measure a line segment that is either vertical or horizontal is simple enough. You can count the distance either up and down the y-axis or across the x-axis.
But what about diagonal lines? How can you know precisely how long the line segment is if it cuts across those tiny boxes? See this example:
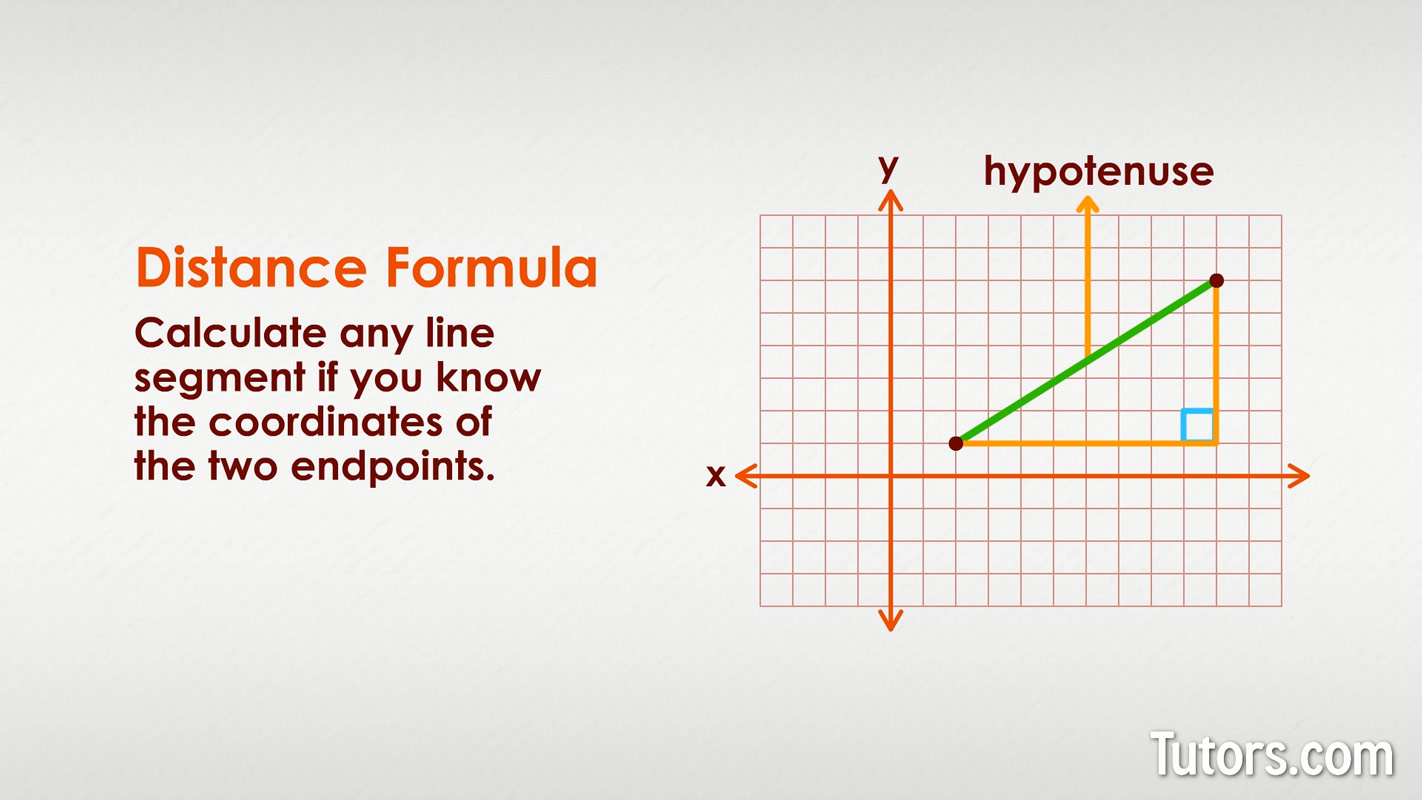
You can use the distance formula to calculate any line segment if you know the coordinates of the two endpoints. You will be mentally constructing a right triangle, using the diagonal as if it were a hypotenuse.
Distance formula
The Distance Formula squares the differences between the two x coordinates and two y coordinates, then adds those squares, and finally takes their square root to get the total distance along the diagonal line:
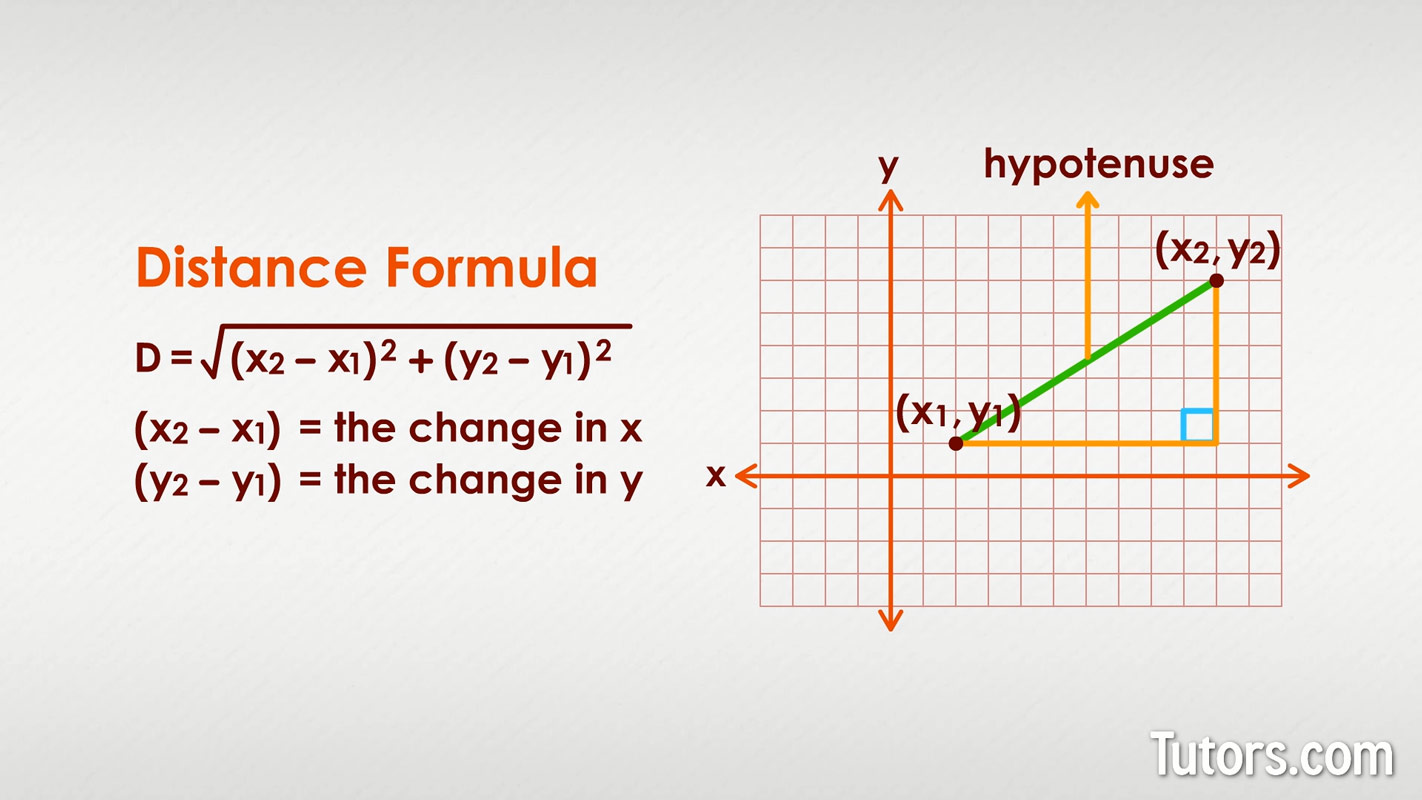
The expression is read as the change in x and is the change in y.
How to use the distance formula
What this is really doing is calculating the distance horizontally between x-values, as if a line segment was forming a side of a right triangle, and then doing that again with the y-values, as if a vertical line segment was the second side of a right triangle.
That leaves a calculation about the hypotenuse, your given diagonal. The distance formula is a special application of the Pythagorean theorem.
All you need to do is plug the coordinates in very carefully. Let's use our line's endpoints, (1, 3) and (7, 6):
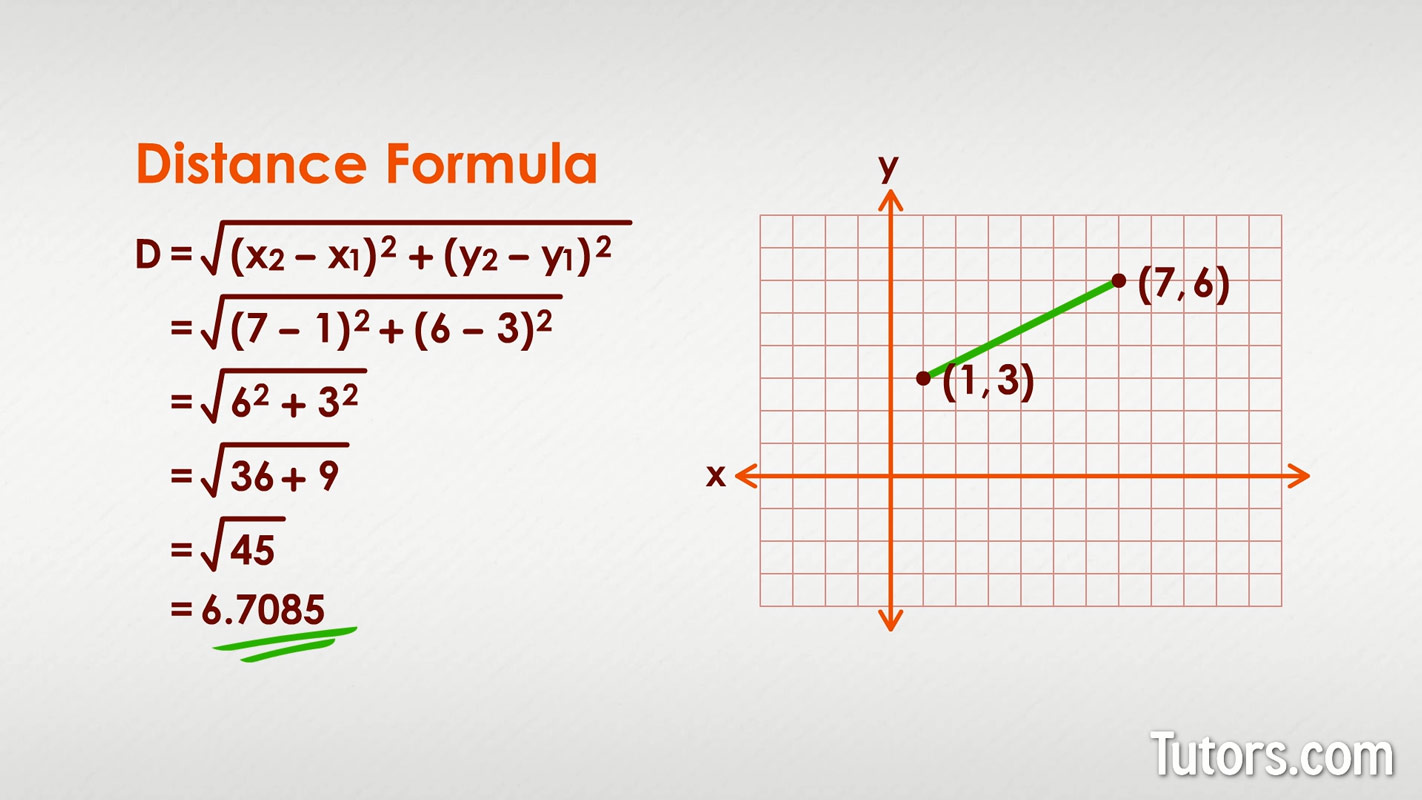
Distance formula examples
You need not even have a coordinate grid in front of you to use the Distance Formula, so long as you have both sets of coordinate points. So, try these three practice problems!
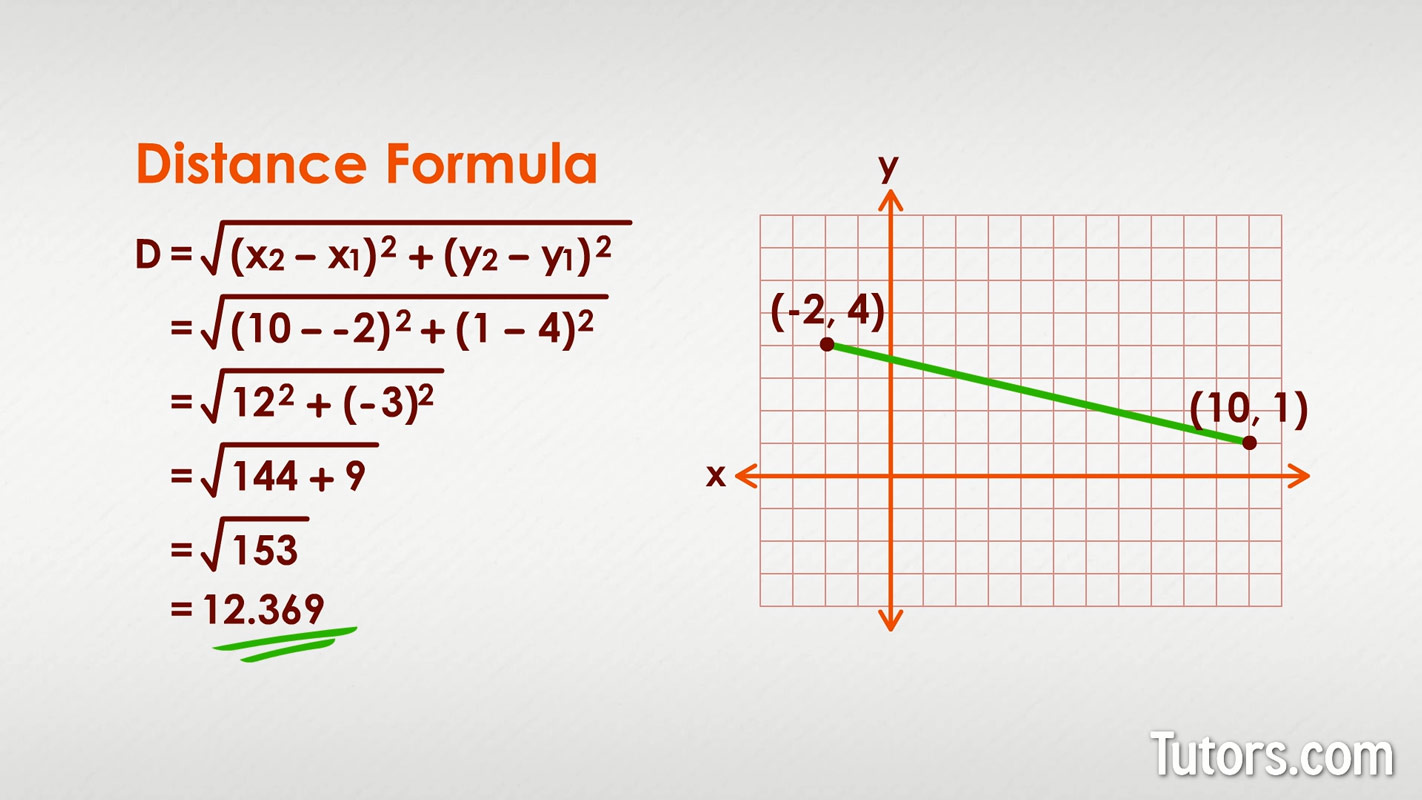
and
and
and
We will not leave you hanging out on a diagonal. Here are the beginning steps, to help you get started:
What comes next?
You really should be able to take the last few steps by yourself. See if you got these answers:
Pythagoras
The distance formula gets its precision and perfection from the concept of using the angled line segment as if it were the hypotenuse of a right triangle formed on the grid.
You need not construct the other two sides to apply the Distance Formula, but you can see those two "sides" in the differences (distances) between x-values (a horizontal line) and y- values (a vertical line).
Lesson summary
Now that you have worked through the lesson and practice, you are able to apply the Distance Formula to the endpoints of any diagonal line segment appearing in a coordinate, or Cartesian, grid. You are also able to relate the Distance Formula to the Pythagorean Theorem.
Pythagoras was a generous and brilliant mathematician, no doubt, but he did not make the great leap to applying the Pythagorean theorem to coordinate grids. To take us from his theorem of the relationships among sides of right triangles to coordinate grids, the mathematical world had to wait for René Descartes.
His Cartesian grid combines geometry and algebra. You can use formulas, including the Distance Formula, to get precise measurements of line segments on the grid.