Area and Perimeter

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

Area and perimeter - formulas for rectangles, squares & circles

You can use area of either a square or circle to find the shape's perimeter (or circumference). With rectangles, if you know only area and one side's length, you can find perimeter. You can even find the lengths of a rectangle's sides if you know area and perimeter. No tricks; just mathematical treats!

Definitions

1. Area is the enclosed space inside a two-dimensional shape. The shape can be a polygon, such as a triangle, square, or rectangle. It can also be a curvilinear shape, like a circle. Area is always measured in square units.

2. Perimeter is the distance around a two-dimensional shape. For polygons, perimeter can be found using only addition by adding the distances as you move around the shape.

3. A circle is the set of all points on a plane that are the same distance from a given point. That set of points closes in a interior space, the area of the circle. The perimeter of a circle is called its circumference.

How to find area and perimeter

Perimeter formulas

• Square –  $P=4s$ (s is the length of any side.)

• Rectangle – $P=2L+2W$ (L and W are the lengths of the sides; length and width).

• Triangle$P=a+b+c$ (a, b, and c are the length of the sides.)

• Right triangle – $P=a+b+\sqrt{{a}^{2}+{b}^{2}}$ (a and b are the lengths of the two legs.)

• Circle – $P=C=2\pi r=\pi d$ (r is the radius and d is the diameter.)

Area formulas

• Square – $A={s}^{2}$ (s is the length of any side.)

• Rectangle – $A=LW$ (L and W are the lengths of the sides; length and width).

• Triangle – $A=\frac{1}{2}bh$ (b is the base and h is the height.)

• Triangle – $A=\sqrt{s\left(s-a\right)\left(s-b\right)\left(s-c\right)}$ (a, b, and c are the side lengths, and s is the semiperimeter.)

• Parallelogram – $A=bh$ (b is the length of the base, and h is the height.)

• Trapezoid – $A=\frac{{b}_{1}+{b}_{2}}{2}h$ (${b}_{1}$ and ${b}_{2}$ are the lengths of the parallel sides, and h is the height or distance between the parallels.)

• Circle – $A=\pi {r}^{2}$ (r is the radius.)

Area and circumference of a circle

For thousands of years, mathematicians have known that circumference is related to the diameter of a circle because of a constant, π, which is the Greek lowercase letter "pi." It has a value in mathematics that never ends and never repeats, but begins 3.1415926535. For everyday mathematics, we usually use 3.1415 or even only 3.14.

Area and circumference of a circle formula

For C = circumference, r = radius, and D = diameter of a circle:

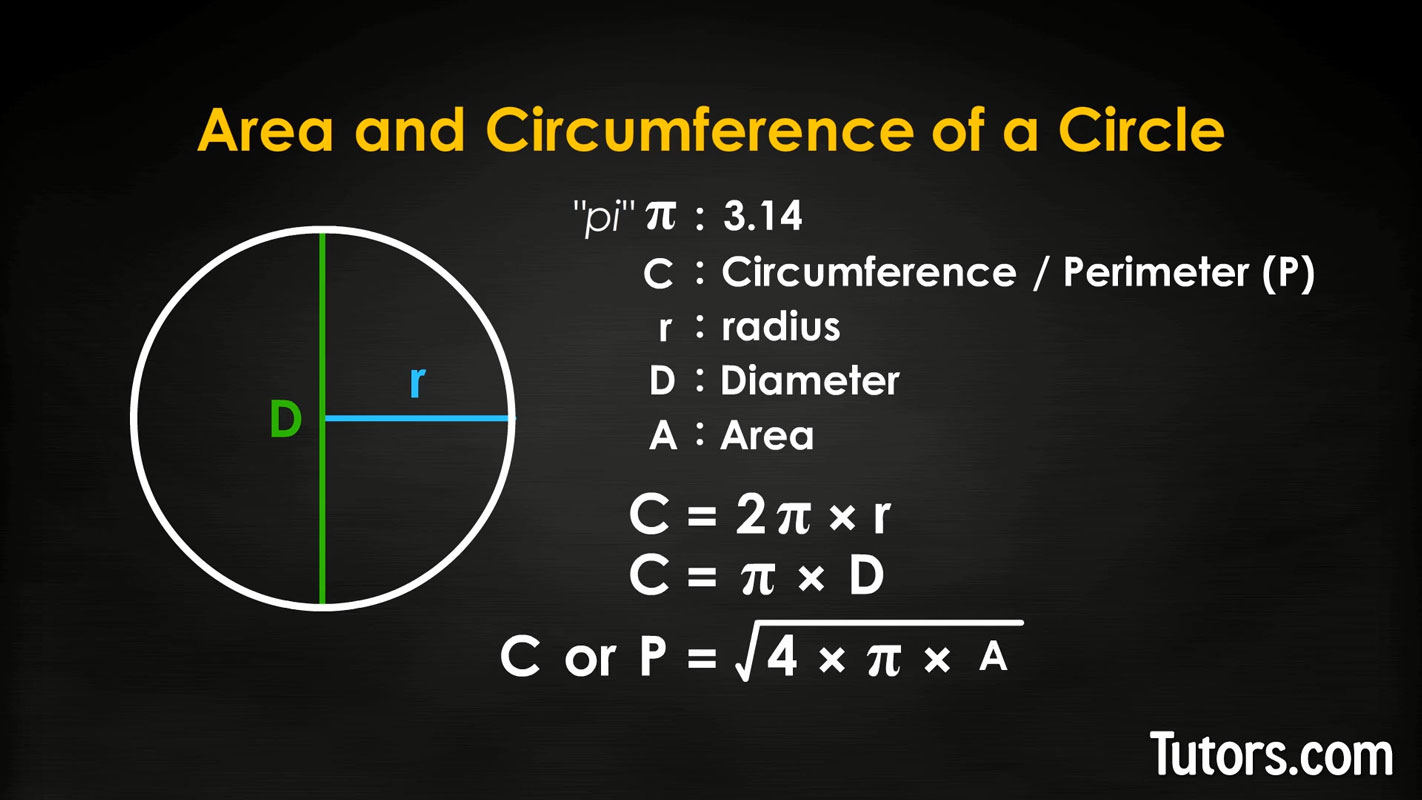
Those two formulas are one of the mathematical "tricks" to finding perimeter if you know area. The formula for the circumference (C), or perimeter (P), of a circle uses π, the area (A) and the square root. Since the calculation involves a square root, you will probably need a calculator:

How to find the area and circumference of a circle

A circle has an area of $\mathrm{31,415}{m}^{2}$. What is its circumference?

Perimeter and area of a square

A square is a polygon; it is a quadrilateral with four congruent sides and four right angles. For squares, you can speed the process of calculating perimeter by multiplying one side's measurement times four, where P is perimeter and a is the length of a side:

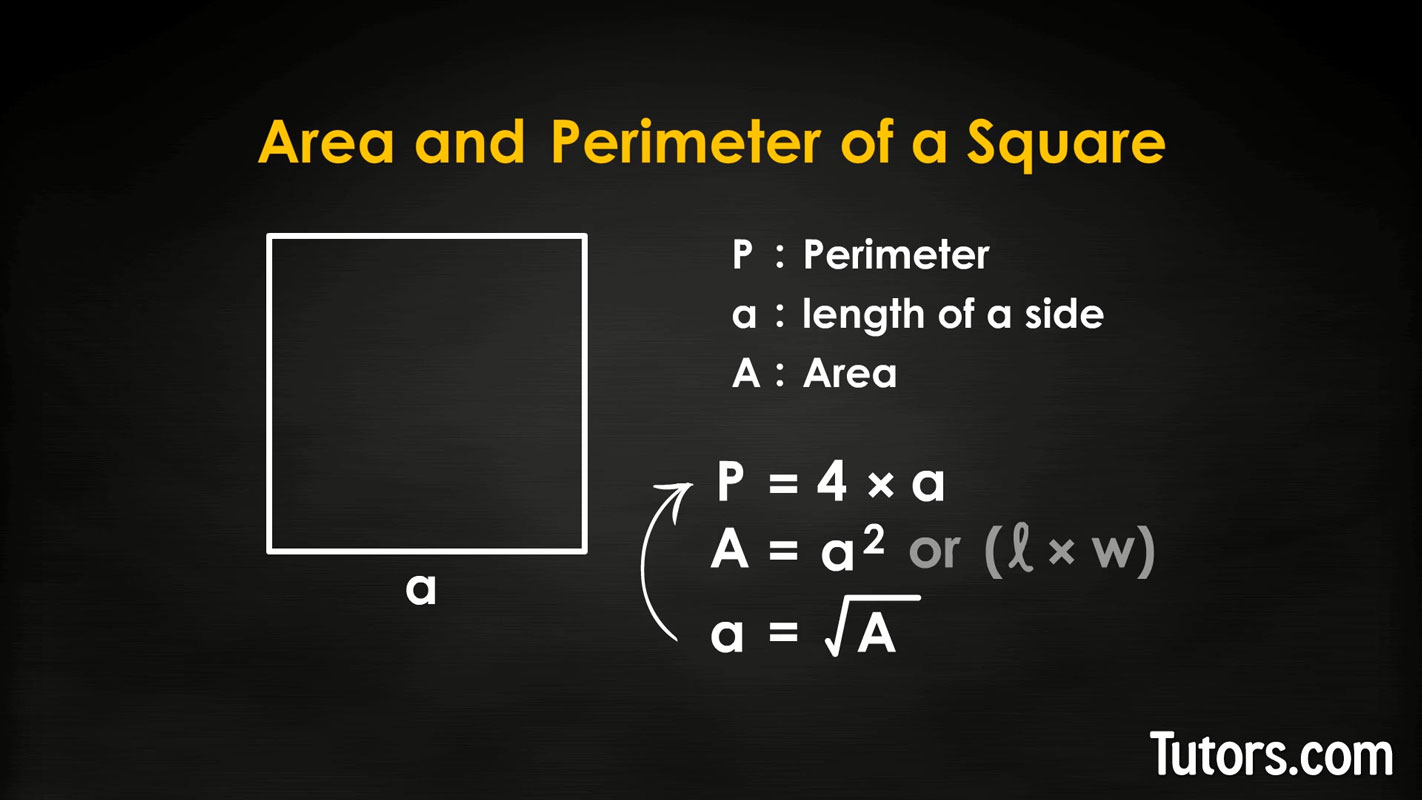
The area (A) is ${a}^{2}$ (length times width). To find the perimeter from area, you first find the square root of A to find the length of any side a:

Then multiply that side measurement times 4 to get your perimeter:

How to find the area and perimeter of a square

The area of a square is 15,129 square millimeters. What is its perimeter?

Then:

Area and perimeter of a rectangle

A rectangle is a polygon; it is a quadrilateral with opposite sides congruent and parallel.

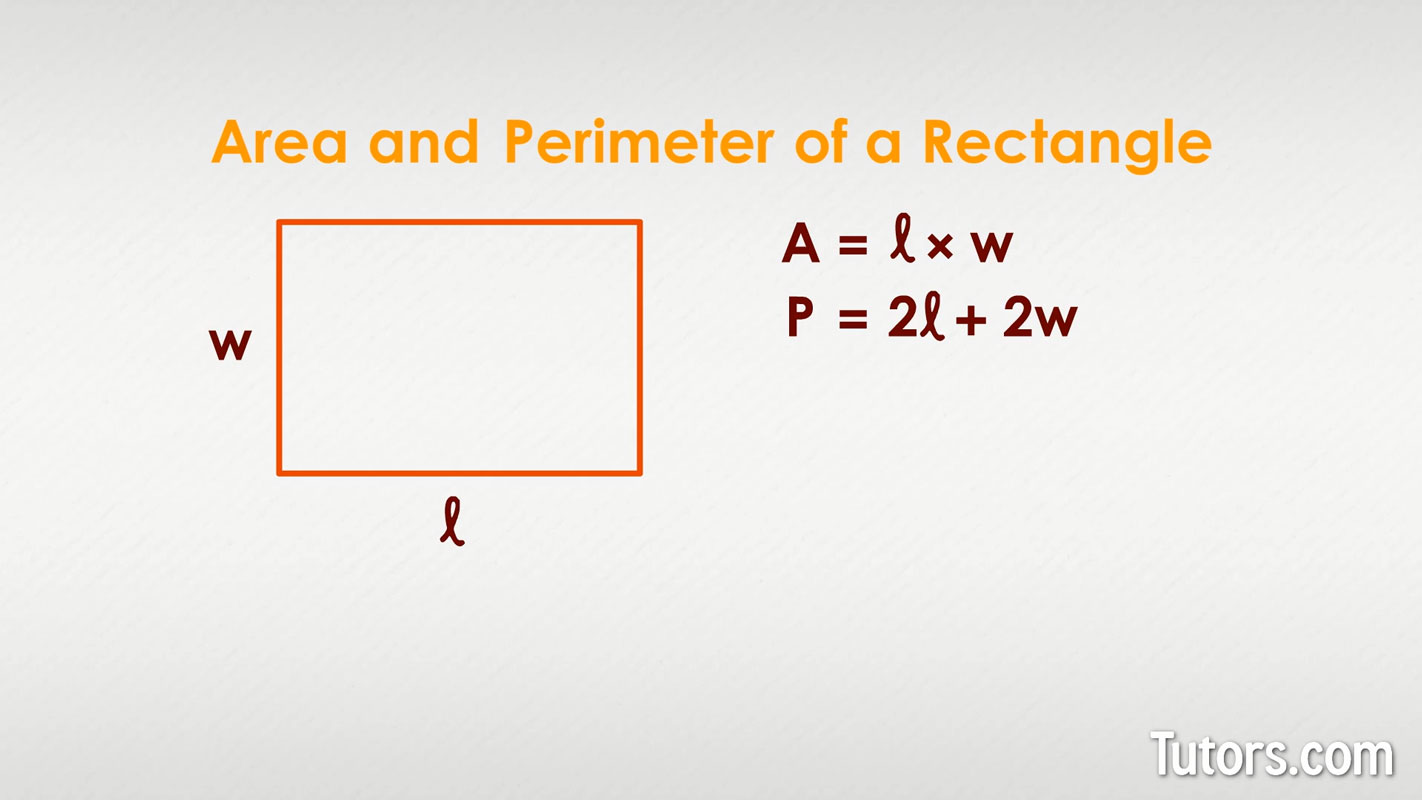
Area of a rectangle

To find the area of a rectangle, you multiply length times width.

Perimeter of a rectangle

To find perimeter:

Since a square is the only rectangle with four congruent sides, you need something more than just a rectangle's area measurement to find perimeter. You need the measurement of any one side.

How To Find the Area and Perimeter of a Rectangle

Use all the information you have in both formulas. Suppose you are given a rectangle with an area of $\mathrm{3,015}c{m}^{2}$ and has one side $45cm$ long.

Then:

Check your work:

You did it correctly!

Finding lengths of sides

You can even find the lengths of a rectangle's sides knowing only perimeter and area. Suppose you have a rectangle with these known values:

Half the perimeter is one length + width, so you know you need two numbers that add together to make 70m, but multiply to make 

• 1 × 1,000

• 2 × 500

• 4 × 250

• 5 × 200

• 8 × 125

• 10 × 100

• 20 × 50

• 25 × 40

Do any of those factor pairs add up to 70?

Yes! 20 + 50 = 70; the length and width must be 50m and 20m!

Lesson summary

Now that you have viewed the drawings and video, and carefully read the notes, you are able to recall and apply the formulas for the perimeter of a circle or square given only the area. You can recall and apply a method for finding either the perimeter of a rectangle given only its area and one length, or the length and width of a rectangle given only the area and perimeter. You also know how to properly format perimeter calculations.