What is a Trapezoid? (Definition & Properties)
What is a trapezoid?
A trapezoid is a quadrilateral with one pair of parallel sides. A trapezoid is:
A plane figure (flat)
A closed figure (it has an interior and exterior)
A polygon (straight sides)
A quadrilateral (four straight sides)
To make a trapezoid, you need a triangle. Any triangle will do: right, obtuse, isosceles, scalene. Slice off the top of the triangle so the cut is parallel to the bottom of the triangle. You now have a tinier triangle and a trapezoid.

Trapezoid definitions
We already know a trapezoid is like the bottom part of a triangle if you cut off a smaller triangle from it. You can also make a trapezoid from four line segments, or four straight objects.
Use anything you like: uncooked spaghetti, pencils, lollipop sticks; whatever you have handy. The four straight (linear) objects can be four different lengths, or three different lengths (two of them could be the same).
Lay two of the objects down, or draw two line segments, so they are parallel (equidistant). Make them horizontal to you. Put the other two objects on the left and right of these two, or draw them in, so all eight endpoints touch.

There you have it, a trapezoid! The horizontal parts are the bases. The last two pieces you drew or put down (at the left and right ends) are called the trapezoid's legs.
Trapezoid angles
The altitude of a trapezoid is its height. Do not be fooled by the sloping legs -- if they slope, they are longer than the height. Altitude is always measured from the base (either parallel side) to the other side, at a right angle to the base.
You can draw a perpendicular line anywhere along the base of the trapezoid, and when it touches the opposite, parallel side, its length is the altitude.
Properties of a trapezoid
Is a trapezoid a parallelogram?
You can identify any trapezoid if it is a quadrilateral with one pair of parallel sides. Many mathematicians include parallelograms as types of trapezoids because, of course, a parallelogram has at least one pair of parallel sides. Other mathematicians exclude parallelograms, saying a trapezoid must have exactly one pair of parallel sides.
Trapezoid shapes
Usually, to be as clear as possible, pictures and drawings of trapezoids show the two parallel sides running horizontally, with the longer side down as the base. Be prepared, though, to see trapezoids in any orientation. A trapezoid can be drawn or pictured with either leg at the bottom, or with the shorter parallel side at the bottom.
Because the parallel sides are the only ones that can be bases, even when the trapezoid is drawn with a leg at the bottom and horizontal, it is not a base. It is still a leg.
The base is usually the longer parallel side, but if the trapezoid is drawn with the shorter parallel side at the bottom, then it is the base.
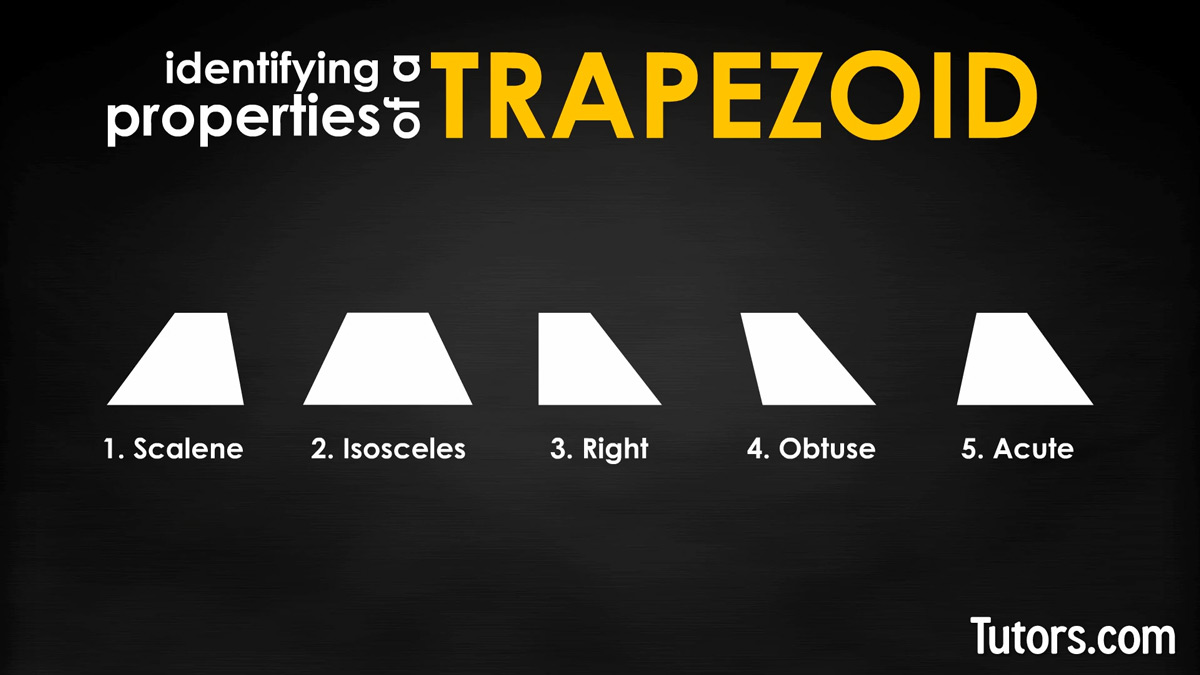
Types of trapezoids
Since trapezoids can begin life as triangles, they share names derived from the kinds of triangles:
Scalene trapezoid – Started out as a scalene triangle
Isosceles trapezoid – Began as an isosceles triangle
Right trapezoid – Once was a right triangle
Obtuse trapezoid – Like an obtuse triangle
Acute trapezoid – Like an acute triangle
Scalene trapezoid
A scalene trapezoid has four sides of unequal length. The bases are parallel but of different lengths. The two legs are of different lengths.

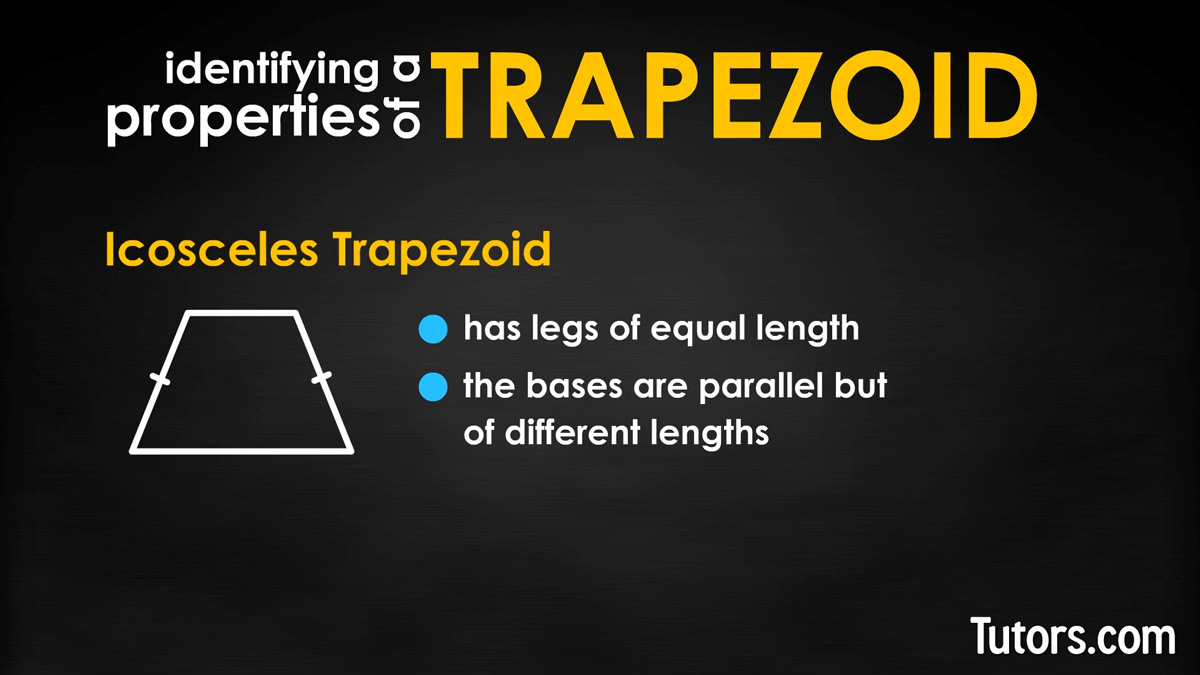
Isosceles trapezoid
An isosceles trapezoid has legs of equal length. The bases are parallel but of different lengths.
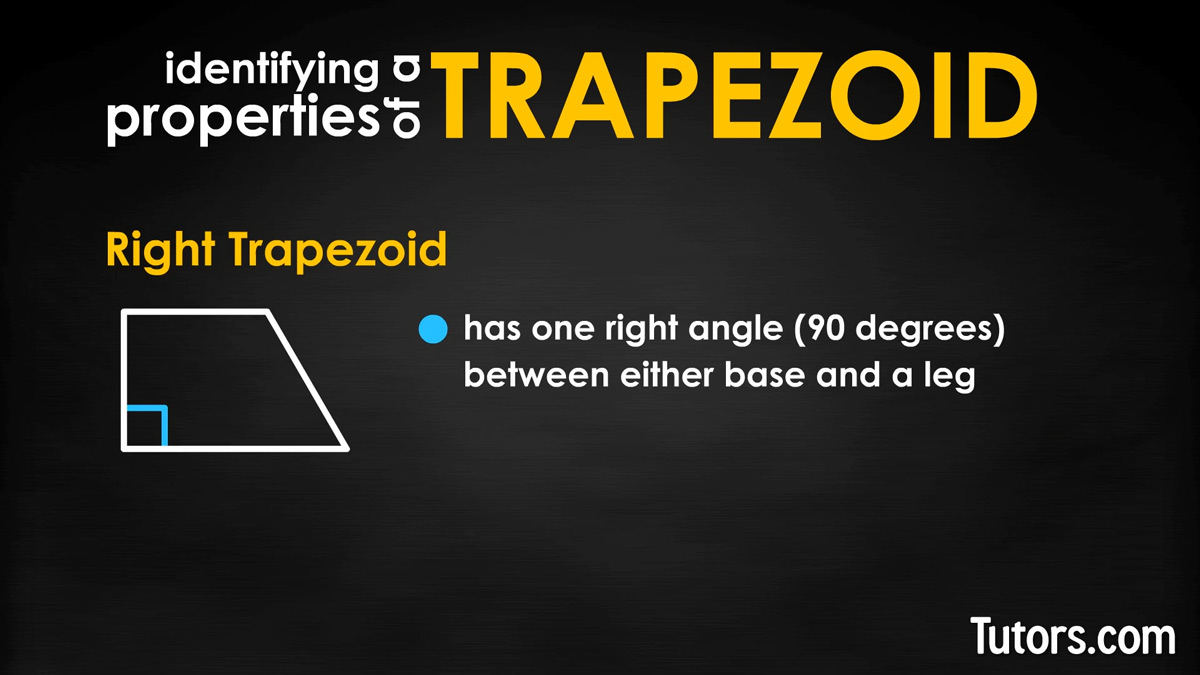
Right trapezoid
A right trapezoid has one right angle (90°) between either base and a leg.
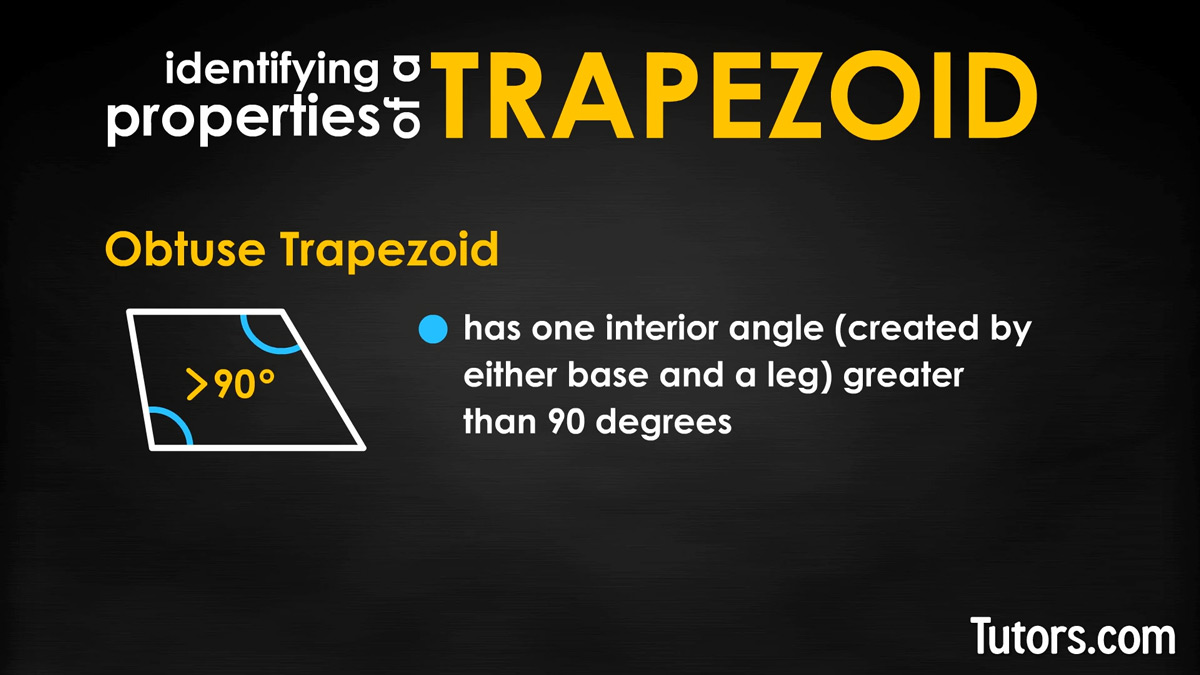
Obtuse trapezoid
An obtuse trapezoid has one interior angle (created by either base and a leg) greater than 90°.
Acute trapezoid
An acute trapezoid has both interior angles (created by the longer base and legs) measuring less than 90°.

Lesson summary
Using just four lines and four interior angles, we have constructed a trapezoid, learned what makes a trapezoid unique (a pair of parallel sides), what the various parts of the trapezoid are, and the names of five special trapezoids.