How To Find the Area of a Trapezoid

Written by

Malcolm McKinsey

January 16, 2023

Fact-checked by

Paul Mazzola

What is a trapezoid?

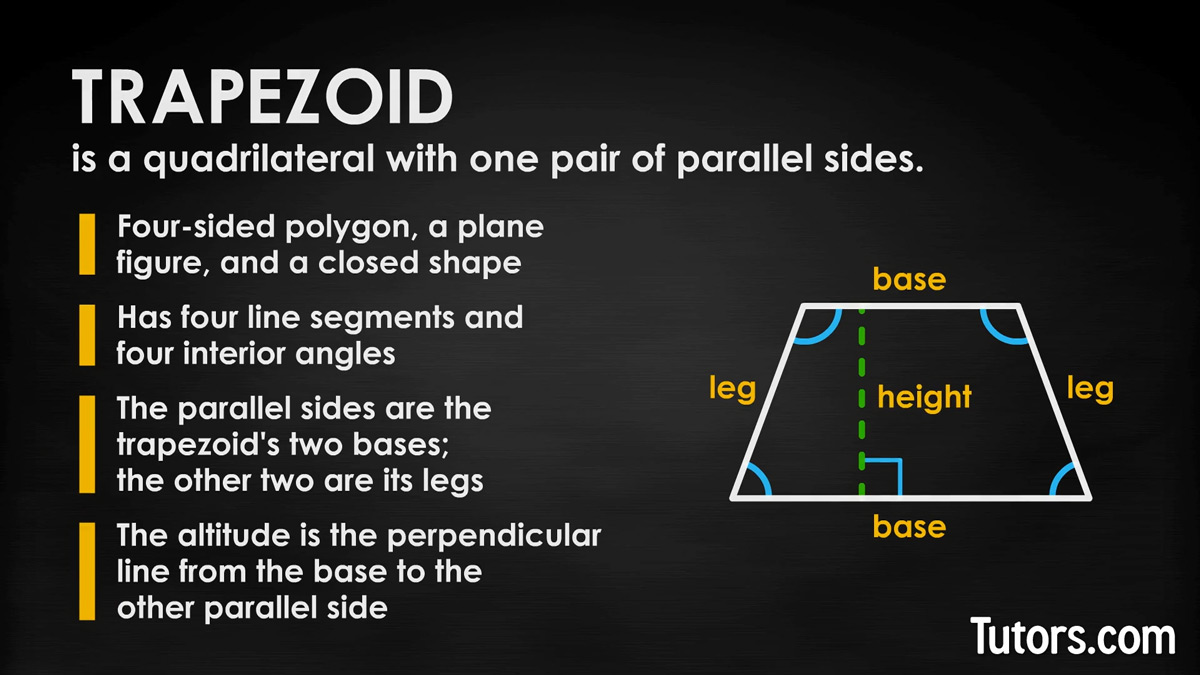
A trapezoid is a quadrilateral with one pair of parallel sides. So, this four-sided polygon is a plane figure and a closed shape. It has four line segments and four interior angles. The parallel sides are the trapezoid's two bases; the other two sides are its legs.

Usually the trapezoid is presented with the longer parallel side -- the base -- horizontal.

A perpendicular line from the base to the other parallel side will give you the trapezoid's height or altitude.

What is an average in mathematics?

In mathematics, an average is the sum of a group of numbers divided by the quantity of items in the group.

So if you have three people holding books, you can find the average number of books they are holding like this:

Martin is holding 5 books, Mack is holding 3 books, and Maria is holding 4 books. Together, 12 books are being held by 3 people.

So, 12 books ÷ 3 people = an average of 4 books each.

How to find the area of a trapezoid

To find the area of any trapezoid, start by labeling its bases and altitude. In our trapezoid, label the longer base aa and the shorter base b. Label a line perpendicular to the two bases h for height or altitude of the trapezoid.

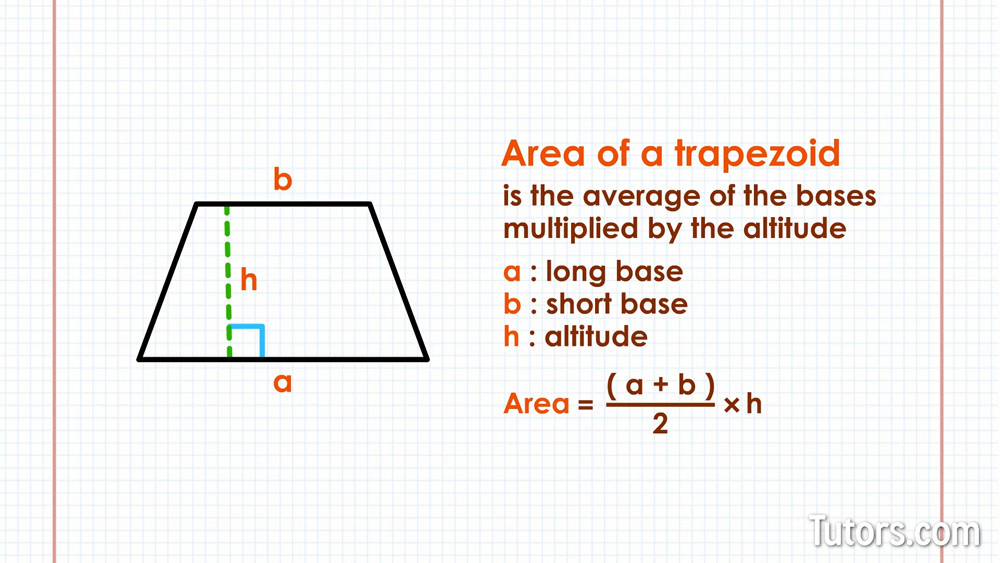
Notice we did not label the legs. We do not need to know anything about the length of the legs or the angles of the vertices to find area.

Area of a trapezoid formula

The formula for the area of a trapezoid is the average of the bases multiplied by the altitude. In the formula, the long and short bases are a and b, and the altitude is h:

Multiplying times $\frac{1}{2}$ is the same as dividing by $2$. We take half the sum of the length of the two bases (their average) and then multiply that by the altitude, or height, to find the area in square units.

Using the area of a trapezoid equation

Trapezoid LMNO has parallel bases LM and NO. Line segment LM is 7 cm long, and line segment NO is 13 cm long. We will label longer side NO as a and shorter side LM as b. The height, h, is 5 cm.

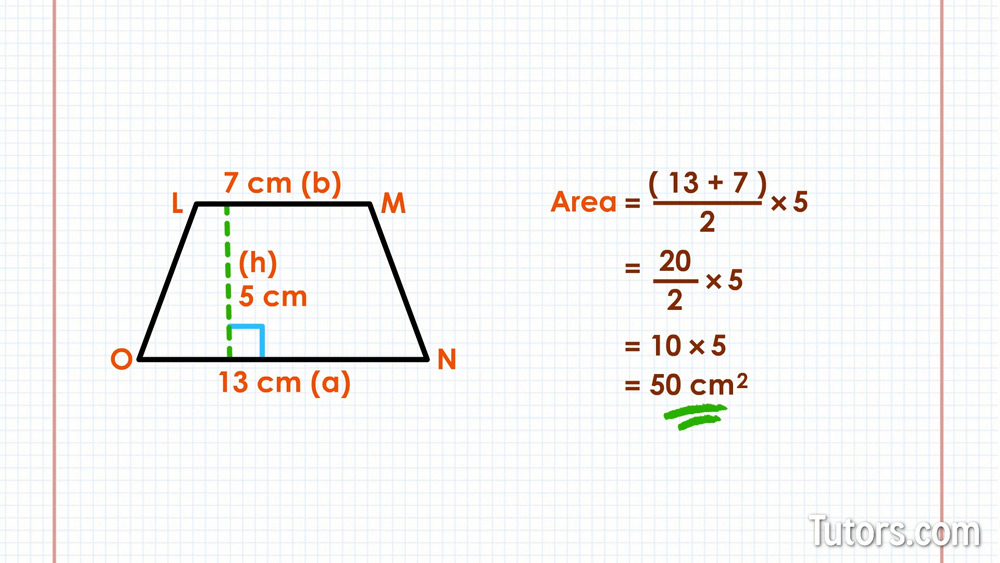
First, let's plug these numbers into our formula:

Next we add 13 plus 7 and get:

Then, we divide by two, then and get:

Finally, we multiply and get our answer:

The area of this trapezoid is 50 square centimeters.

Area of a trapezoid examples

Now you try it! Another trapezoid has a long base a, 11 meters, and a shorter base b, 7 meters. Its altitude h is 9 meters. What is the area in square meters?

Did you get 81 square meters? Your answer for area is always in square units of the linear measurement.

So a trapezoid measured in feet gives an area in square feet, centimeters yield square centimeters, and so on.

Because of the commutative property of multiplication, you can rearrange these three numbers, $\frac{1}{2}$, altitude h, and the length of bases a + b, in any order to make the calculation easy.

So, with trapezoid LMNO, you could also have written the formula like:

Example #2

Here is one more example for you. The new trapezoid is upside down from how you usually see them, but don't let that stop you! The short base b is 21 inches long. The long base a (this time at the top of the drawing) is 31 inches long. The altitude h (no matter which way you look at the trapezoid) is 5 inches.

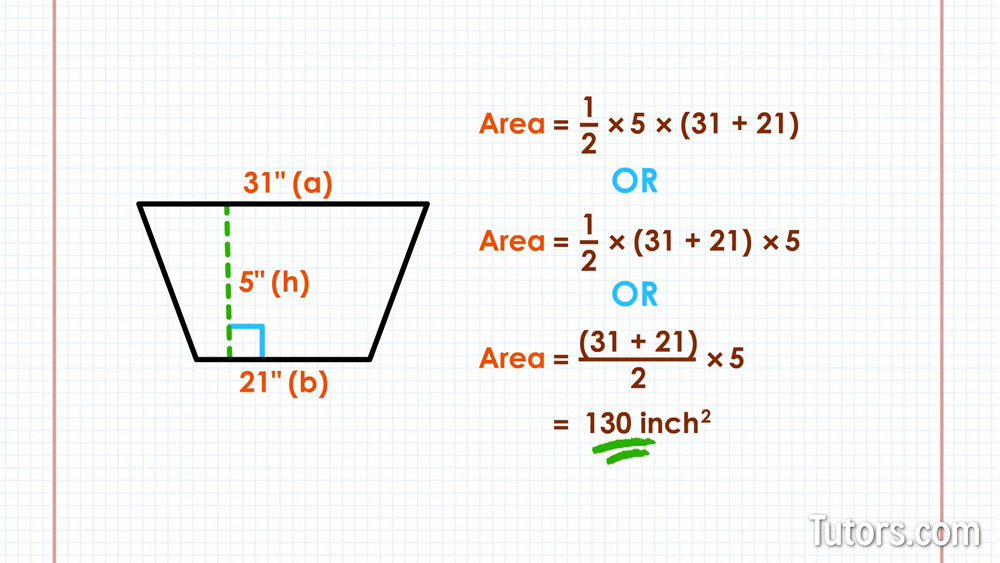
The formula can look like either of these:

• $area=\frac{1}{2}\times 5\times (31+21)$

• $area=\frac{1}{2}\times (31+21)\times 5$

• $area=\frac{31+21}{2}\times 5$

However you use the formula, you will always get the same answer: $area=130i{n}^{2}$

Lesson summary

In this lesson and video we have reviewed what a trapezoid is, examined how averages have a role in geometry, learned how to label and use the parts of a trapezoid to calculate area, and learned the formula for calculating the area of a trapezoid in square units.