Quotient — Definition, How to Find, Examples

What is a quotient?

The quotient is the answer to any division problem. The word comes from a Latin word, quotiens, which means “how many times,” as in, “how many times does 8 go into 65? The number of times 8 goes into 65 is the quotient or the result of a division problem.

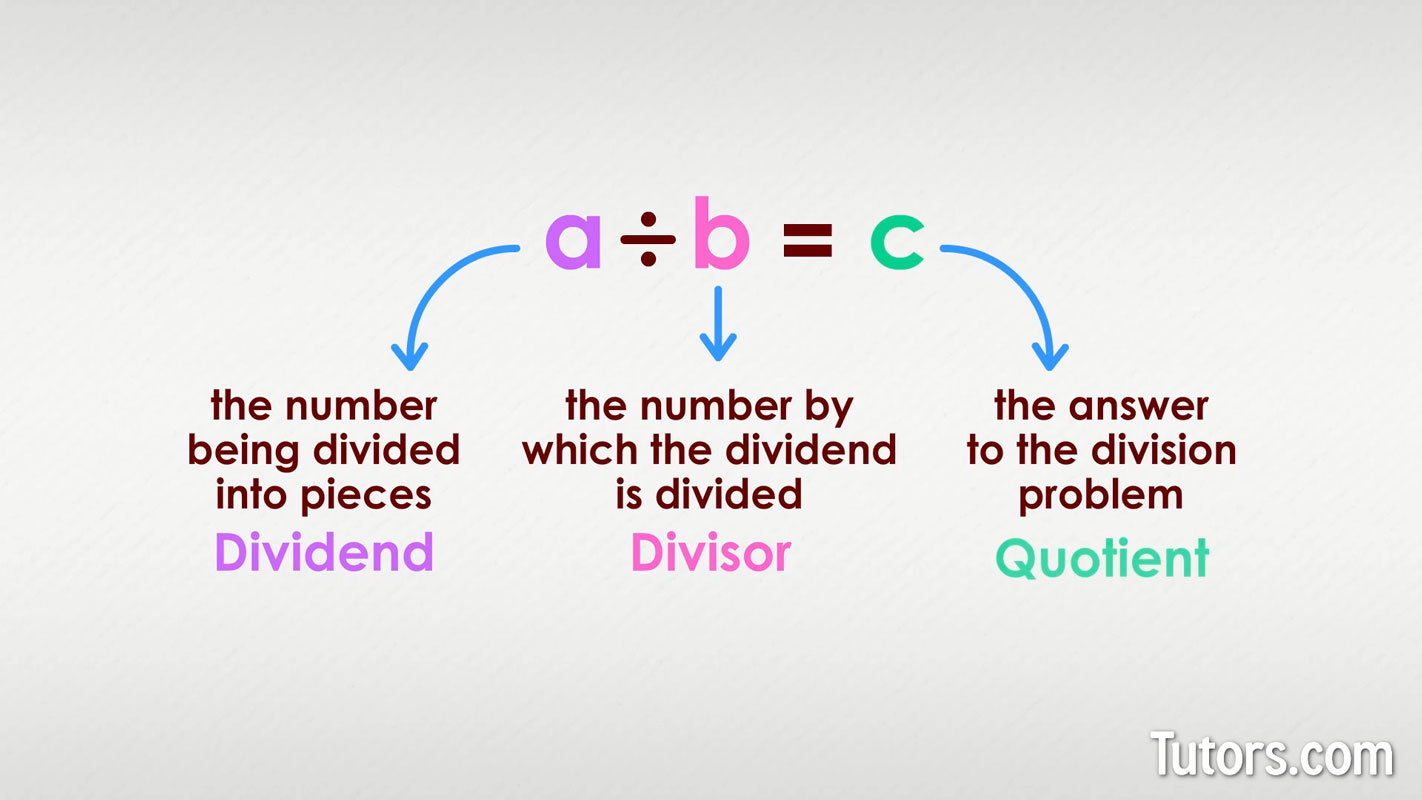
Parts of a division problem

In a division problem, the number being divided into pieces is the dividend. The number by which the dividend is divided is called the divisor. And the answer to the division problem is the quotient.

Here are the parts for the simple division problem, ten divided by two:

• 10 (dividend) ÷ 2 (divisor) = 5 (quotient)

Where does the quotient go?

When using short or long division, the dividend goes under the division bracket, ⟌ , the divisor goes to the left of the bracket, and the quotient goes on top of the bracket aligned by place value with the dividend.

The division symbol, ÷, is called an obelus. It is used in division number sentences. The obelus follows the dividend and precedes the divisor.

How to find the quotient of a number

Setting up a division problem is a key first step to dividing correctly. First, decide which number is to be divided. That is the dividend. Place it under the division bracket.

The dividend is divided by some other number; that is the divisor, and it goes to the left of the bracket. Perform the division. Your answer is the quotient. Any remainder is placed to the right of the quotient.

Finding the two given parts (dividend and divisor) is often challenging in a word problem, but in a number sentence, these parts stand out. Here is an example sentence:

• 25 ÷ 5 = ?

• Dividend (obelus) divisor (equal sign) quotient

In this case, our answer would be the whole number 5. So, the number 5 is one example of a quotient. We will go over more complicated examples of quotients later in the lesson.

Quotient and remainder

When you compute the quotient in division, you may end up with a remainder. The result of division is called the quotient. The number left over is called the remainder. The remainder is part of the result.

Here is a quotient example with a remainder:

• $\frac{34}{8}$ = 4 and 2 remainder = 4.2

8 goes into 34 four (4) times, which is 32. That leaves us with 2 remaining.

How to find the quotient of a fraction

Fractions are already division problems. The fraction bar separating numerator and denominator is signaling division:

• $\frac{3}{12}$ = 3 ÷ 12 = ?

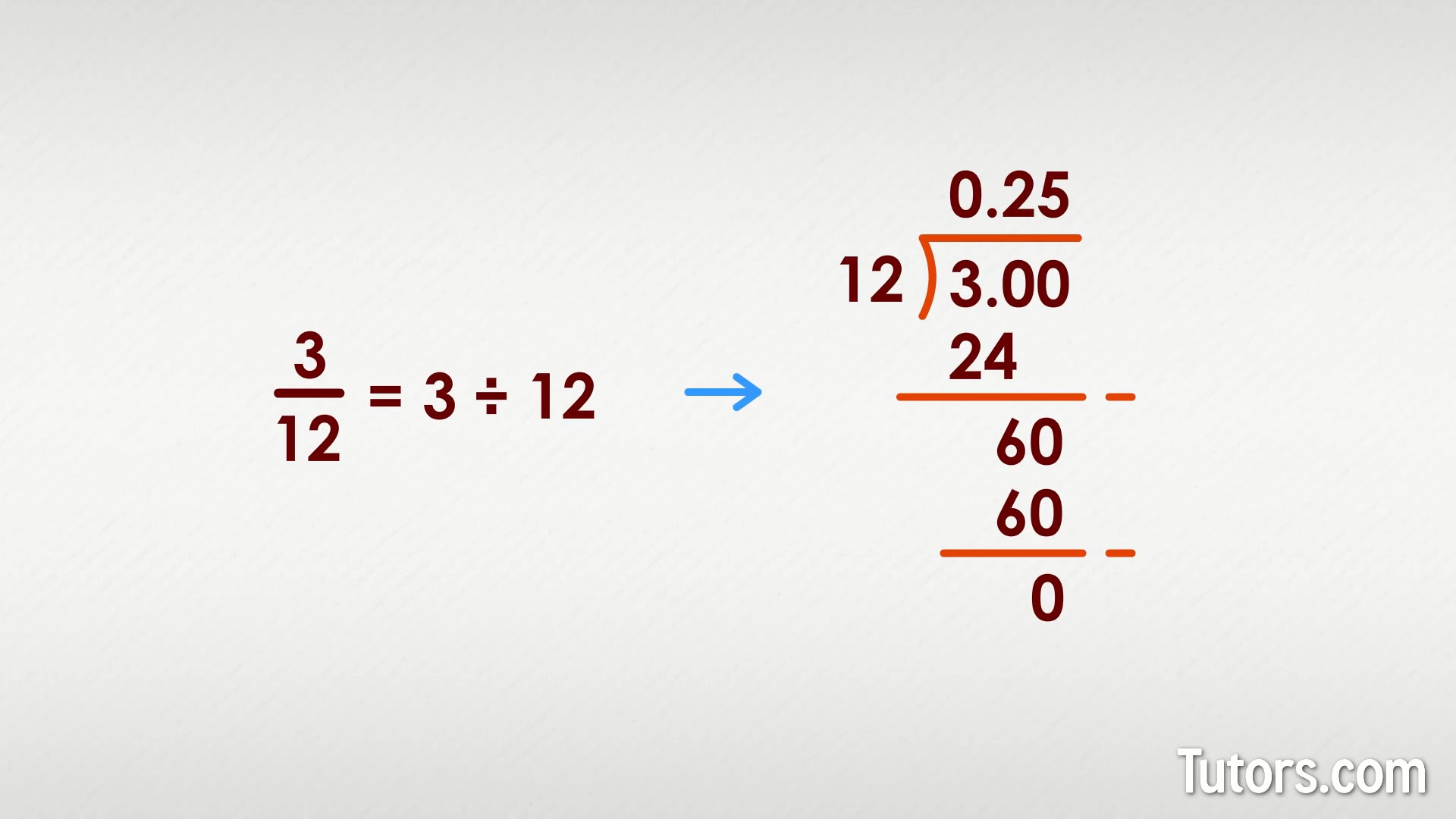
Quotient of two fractions

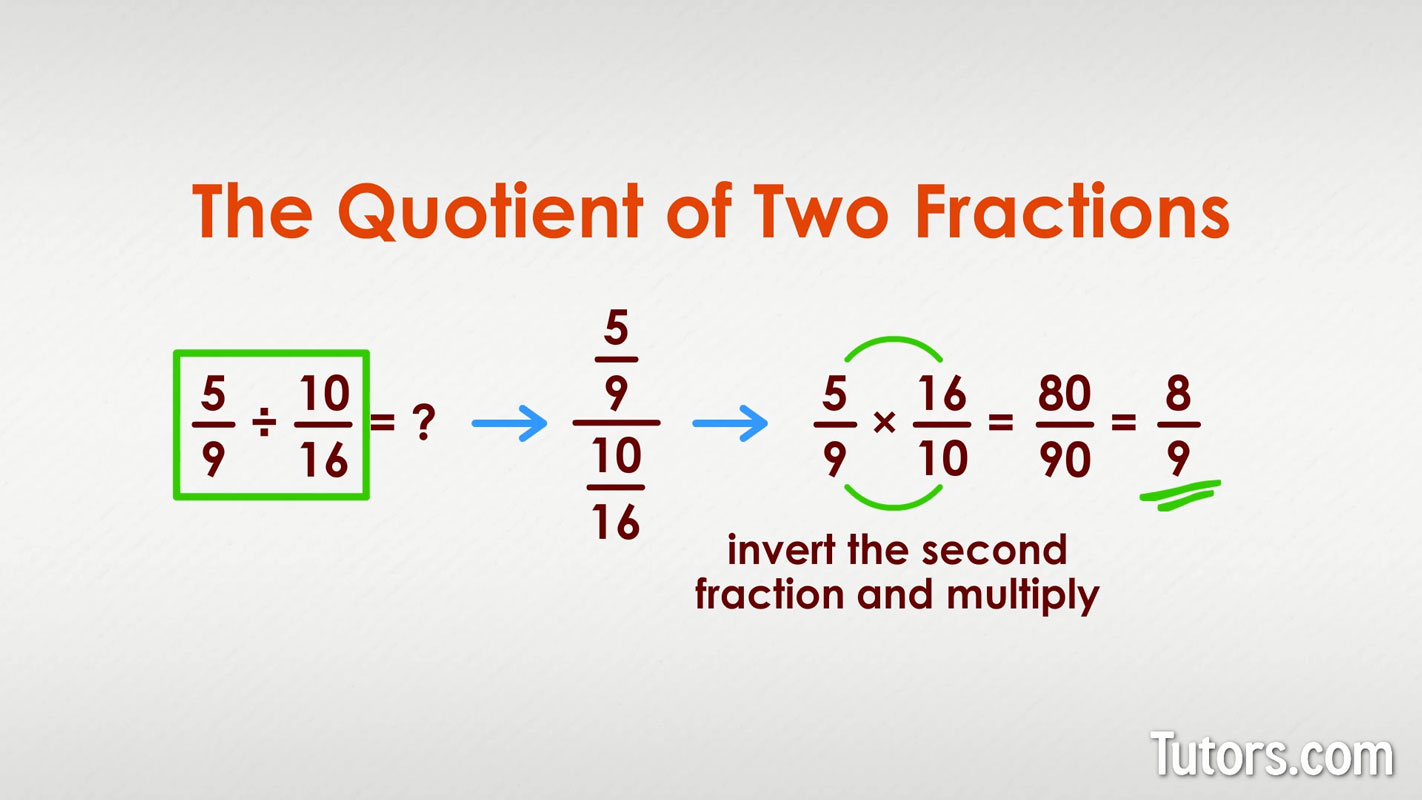
A more complicated search for a quotient can occur when you are dividing two fractions:

Such a problem can also appear in this form:

Recall the process for dividing fractions; invert the second fraction and multiply:

The quotient for $\frac{5}{9}\div \frac{10}{16}=\frac{8}{9}$

Division quotients in algebra

Quotients appear in algebraic expressions, too. You can divide one monomial by another:

The variable b in the numerator and denominator cancel out (think: 

). And the numbers divide readily, leaving you with 3a as the quotient.

You can also divide a polynomial by a monomial:

You have the polynomial $27{x}^{2}+36x$ being divided by a monomial, 9x.

First, separate the two terms in the numerator and divide each by the denominator.

This gives you 3x for the first term ($\frac{27{x}^{2}}{9x}$) and 4 for the second term ($\frac{36x}{9x}$):

One polynomial can be divided by another polynomial to get a quotient, too:

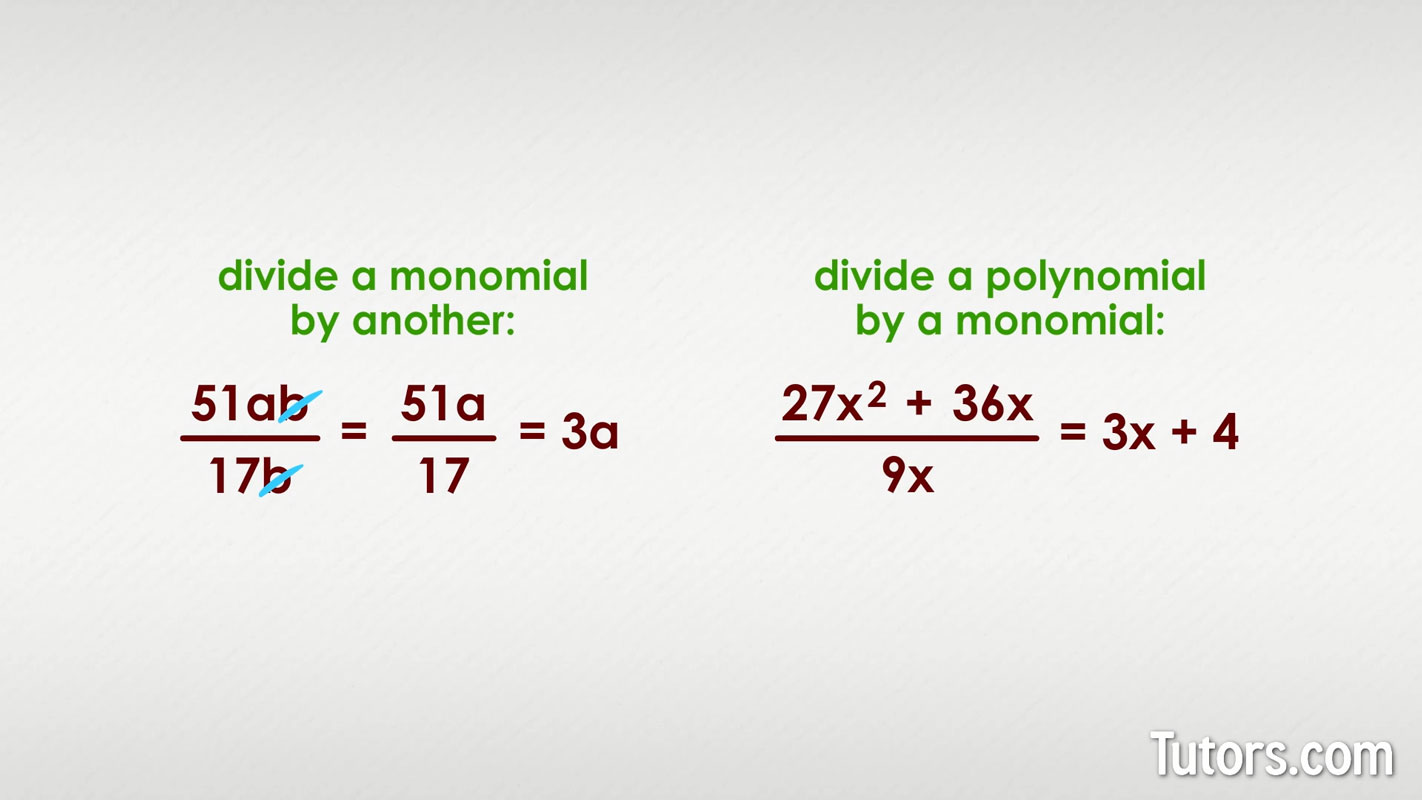
What is a partial quotient?

Partial quotient is a division method (also called chunking) that uses repeated subtraction to solve simple division problems. The partial quotients method is used when dividing a large number by a small number.

Instead of trying to figure out how many times 12 goes into 250, you can turn it into a simpler multiplication problem and multiply 12 by an easy multiple like 10, which gives you 120. The number 10 becomes your partial quotient, and you subtract 120 from the divided, 250.

You repeat this step reducing the dividend by chunks until it is reduced as much as it can be by 12. At the end, you add up your partial quotients, and the result is your quotient.