Mean, Median, Mode & Range — Definitions & How To Find

Written by

Malcolm McKinsey

January 12, 2023

Fact-checked by

Paul Mazzola

What is mean, median, mode, and range?

Mean, median, and mode are measures of central tendency used to summarize numbers in a data set. Mean, median, and mode help you approximate the center or central number(s) of a data set. The range is the measure of dispersion in a data set.

• Mean – The arithmetic average of the numbers in a data set.

• Median – The central value in a data set when the numbers are arranged least to greatest.

• Mode – The most commonly appearing value in a data set

• Range – The difference between the largest and smallest number in a data set.

For most math problems, the mean, median, mode, and range provide plenty of summary data.

How to find the mean, median, mode, and range

To find the mean, median, mode, and range, you need a set of numbers and the ability to do simple addition, subtraction, and division.

Data sets can be tightly clustered around a repeated value, like these numbers:

Or they can be dispersed, like these values:

In both cases, you can summarize the data by noting which values tend toward the middle of the set of numbers by finding the mean, median, mode, or range.

How to find the mean

The arithmetic mean of a data set is an average. The mean is revealed by summing the individual numbers in the set, then dividing the sum by the number of numbers in the set, like this:

For this set:

First, sum the numbers:

Then, divide the sum by how many numbers are in the set:

The mean of our data set is 2.

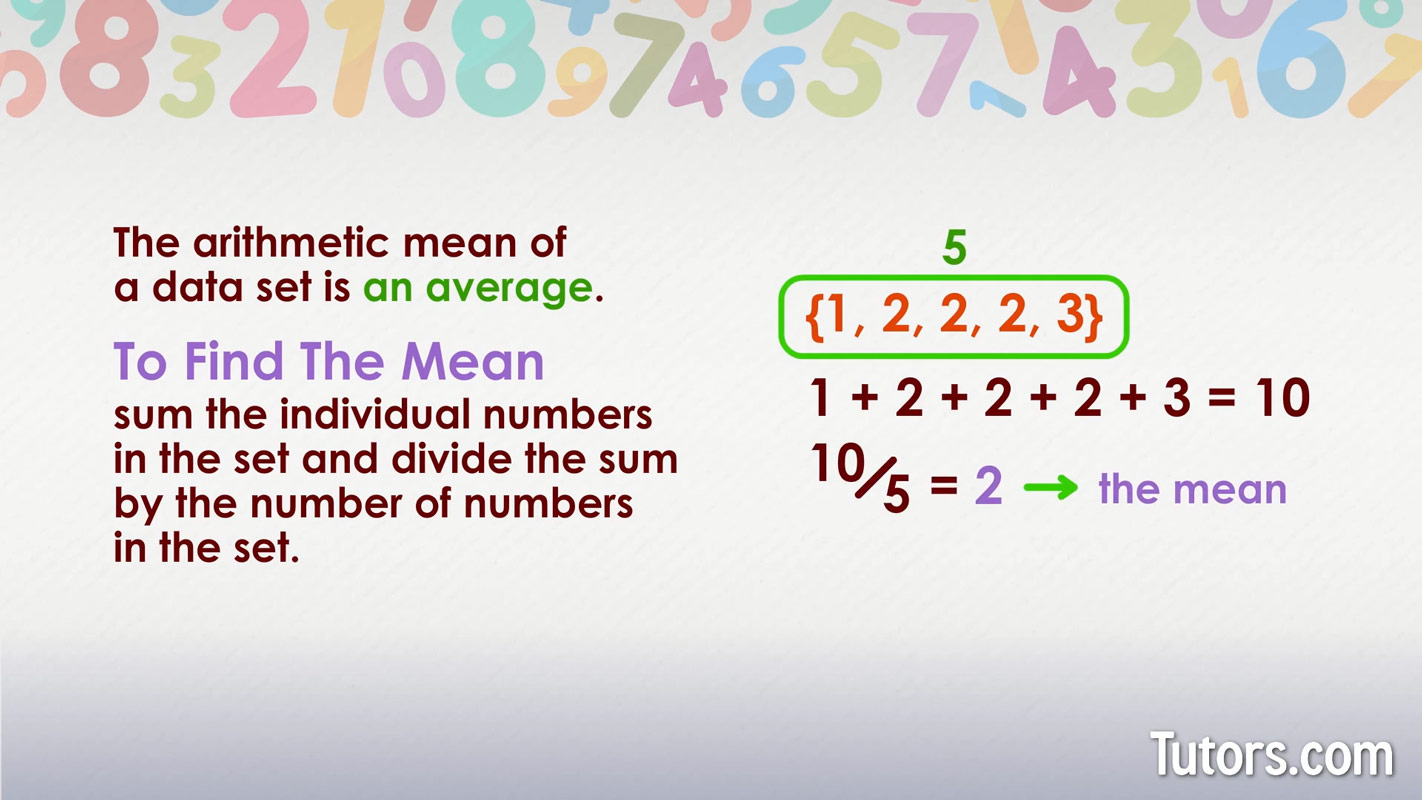
Here is another example data set. What is the mean of this set?

We sum the numbers:

And then divide by the number of numbers in the set, which is 7:

The mean or average of this data set is 8.

Whole numbers are not the only set of numbers for which you can find a mean:

How to find the median

The order of the list of numbers matters when calculating the median. The median is the middle value in a data set when the data are arranged from least to greatest, like these sets:

The first two data sets easily show their medians or middle numbers. For the first data set, with five values, the center value is 2.

For the second data set, with seven values, the middle value is 6. So, the two medians for the two data sets are 2 and 6.

Finding the middle number of a data set with an odd number of values is straightforward.

The last data set, however, has an even number of values, six. To calculate the median from an even quantity of numbers, take the mean of the center two numbers.

The two middle numbers are 91 and 104. We sum them, and then divide by 2:

The median value or middle number of our third data set is 97.5.

Almost always, when finding the median of an even quantity of numbers, the calculated median will not be a number in the set.

It could happen, though, like in this example:

The median here is 37, which is a number in the original data set.

Median is especially useful when your data set has outliers or numbers far away from the middle of the group of numbers. Outliers can drastically skew your central tendency causing your summary data to be less accurate.

The effect of outliers can be diminished by paying more attention to the median than to the outliers.

If you have navigated through the first two measures of central tendency, we have great news for you; the other two measures are far easier to understand and calculate.

How to calculate mode

The mode of a data set is the quantity appearing the most number of times. Unlike the other measures of central tendency, a mode is not a requirement of a data set. On the other hand, a data set can have multiple modes.

Here is a set of numbers with an obvious mode:

The mode is 2. It appears more than the other quantities. Here is a data set with no mode:

This data set has no mode because no number appears more than any other.

And here is a set of data points with multiple modes:

We immediately see that 35, 104, and 502 all appear twice. They are the three modes of the data set.

How to find the range of a data set

The range of a data set is the difference between the largest value and smallest value. To calculate the range, subtract the lowest value from the highest value.

Here is a data set:

You subtract the smallest number from the largest number in the set:

The range of the data set above is 610.

When finding the range, you do not have to arrange your data set in numerical order, but if you have a large number of data points, it will make it easier to see which numbers you need to subtract.

Calculate mean, median, mode, and range

Here are six mean, median, and mode example problems for you to solve:

1. Find the mode in this data set: {11, 11, 14, 14, 14, 16, 17}

2. Identify the range of this data set: {1.1, 6.7, 9.5, 17.8}

3. Calculate the median for this data set: {5, 5, 23, 891, 892}

4. Find the mean of this data set: {5, 5, 23, 891, 892}

5. Find the mean, median, mode, and range of this data set: {1, 3, 7, 9, 9, 13, 17, 99}

6. Identify the mode of this data set: {1, 2, 3, 4, 5}

Before you peek, check your answers. Take your time!

1. The mode is 14

2. The range is 16.7

3. The median is 23

4. The mean is 363.2

5. The mean is 19.75, the median is 9, the mode is 9, and the range is 98

6. No mode exists. Each number appears only once.