Types of Polygons
What is a polygon?
Polygons are some of the first shapes we learn to draw as children, and they appear all around us. Polygons can be regular or irregular. They can be simple or complex, convex or concave. They can be the familiar shapes you see in geometry textbooks, or they can be strange shapes, like darts and bowties.
The word "polygon" means "many-angled," from Greek. To be a polygon, a flat, closed shape must use only line segments to create its sides. So a circle or any shape that has a curve is not a polygon.
The three identifying properties of any polygon are that the polygon is:
A two-dimensional shape
Closing in a space (having an interior and exterior)
Made with straight sides
Types of polygons
Let's take a look at the vast array of shapes that are polygons and go into detail.
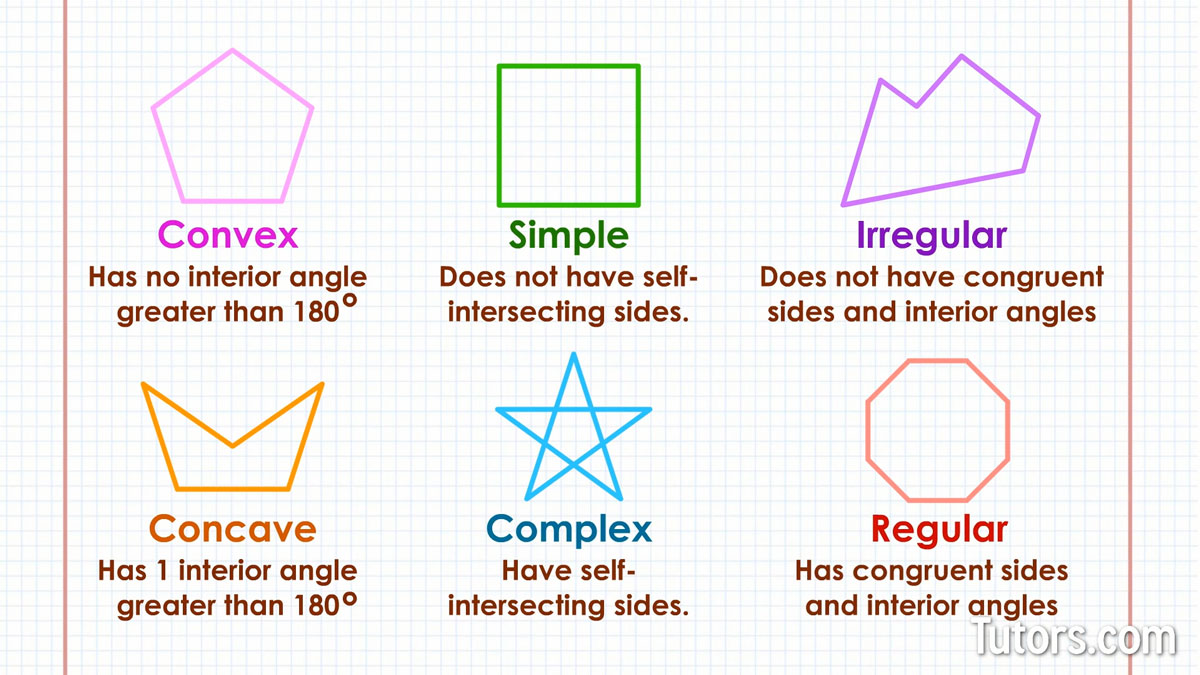
A convex polygon has no interior angle greater than 180° (it has no inward-pointing sides). A concave polygon has one interior angle greater than 180°.
A simple polygon encloses a single interior space (boundary) and does not have self-intersecting sides. Complex polygons have self-intersecting sides!
An irregular polygon does not have congruent sides and interior angles.
A regular polygon has congruent sides and interior angles.
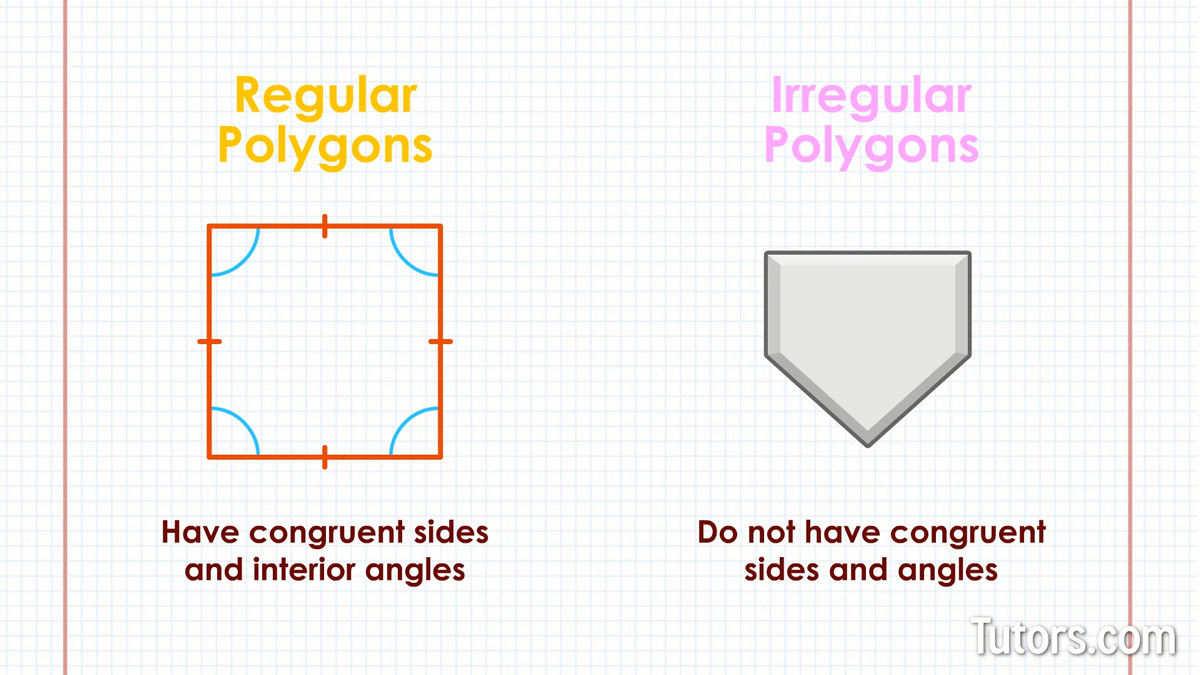
Regular and irregular polygons
Regular polygons have congruent sides and interior angles. Every side is equal in length to every other side, and every interior angle is equal to all other interior angles. The number of regular polygons is limitless.
Irregular polygons do not have congruent sides and angles. Home plate on a softball or baseball field is an irregular pentagon, because it has five sides with two 90° angles.
Convex and concave polygons
A convex polygon closes in an interior area without looking "dented." None of its interior angles point inward. In geometry, you could have a four-sided polygon that points outward in all directions, like a kite, or you could have the same four sides so two of them point inward, forming a dart. The kite is convex; the dart is concave.
Every interior angle of a convex polygon is less than 180°. A concave polygon has at least one angle greater than 180°. Think of a bowtie-shaped simple hexagon (6 sides). It will have two interior angles greater than 180°.
Simple and complex polygons
Simple polygons have no self-intersecting sides. Complex polygons, also called self-intersecting polygons, have sides that cross over each other. The classic star is a complex polygon. Most people can doodle a star on paper quickly, but few people label it a pentagram, complex polygon, or self-intersecting polygon.
The family of complex star-shaped polygons generally share the Greek number prefix and use the suffix -gram: pentagram, hexagram, octagram, and so on.
You cannot draw a complex triangle. For every polygon with four or more sides, a complex polygon can be drawn. A complex quadrilateral is that familiar bowtie shape, but it is considered to have only four sides, because one pair of opposite sides has twisted to cross each other.
Just as you do not count the crossed sides as four line segments, you do not count the two angles they create as interior angles. The complex quadrilateral still only has four sides and four interior angles.
Complex polygons may be hard to imagine unless you think of them with elastic sides. If you could lift part of the polygon up and twist it, so two sides cross one another, and then put it down flat again, you would have a complex polygon. Because you twisted two sides, you still have those two sides (they do not double in number by crossing). They also do not create new vertices where they cross.
Antiparallelogram
An unusual complex polygon is the antiparallelogram, which looks a bit like bird wings. An antiparallelogram (or crossed parallelogram) has the normal two pairs of congruent, opposite sides, but one pair has been crossed, forming what appears to be two touching triangles.
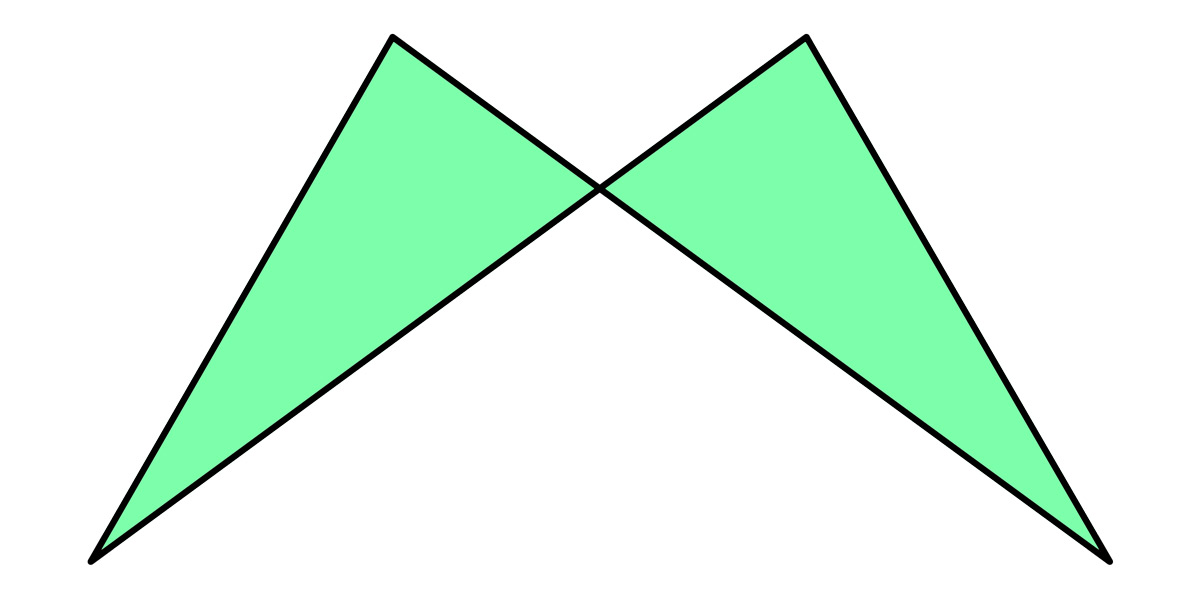
Like any parallelogram, though, the antiparallelogram still only has four sides and four interior angles. Its diagonals, however, lie outside the shape!
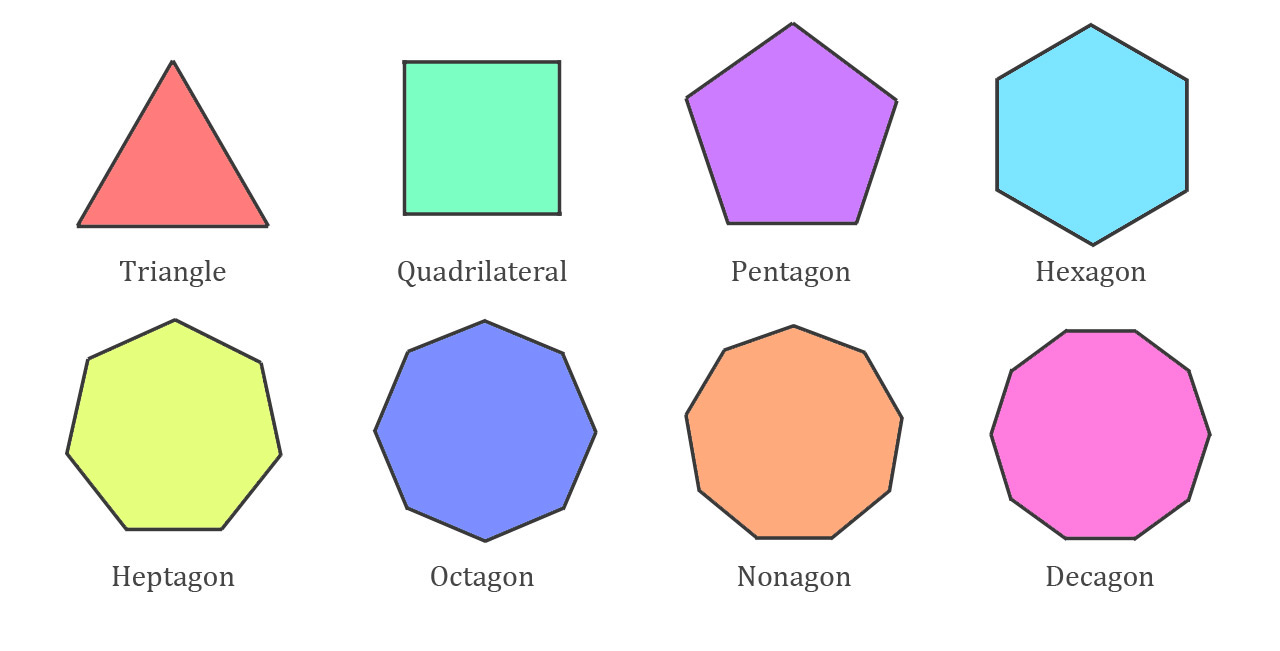
Names of polygons
| Polygon Shape | Number of Sides |
|---|---|
| Triangle | 3 sides |
| Square | 4 sides |
| Rectangle | 4 sides |
| Quadrilateral | 4 sides |
| Parallelogram | 4 sides |
| Rhombus | 4 sides |
| Dart | 4 sides |
| Kite | 4 sides |
| Pentagon | 5 sides |
| Hexagon | 6 sides |
| Heptagon | 7 sides |
| Octagon | 8 sides |
| Nonagon | 9 sides |
| Decagon | 10 sides |
| Dodecagon | 12 sides |
| Icosagon | 20 sides |
| Hectagon | 100 sides |
| n-gon | n sides |
Is it a polygon?
The interiors of all polygons can be broken up into triangles, which is a handy way to find the sum of their interior angles. Take two less than the number of sides, n, and multiply times 180°: (n - 2) x 180°.
A circle is not a polygon, but a icosikaihenagon is a polygon. An icosikaihenagon is a 21-sided polygon. Most mathematicians and mathematics students would simply write "21-gon" to name it.
Lesson summary
Polygons can be studied and classified in many different ways. You now see that polygons can be regular or irregular, convex or concave, and simple or complex. When you see an unfamiliar polygon, you can determine its properties and classify it correctly.
To be a polygon, the shape must be flat, close in a space, and be made using only straight sides. Polygons with congruent sides and angles are regular; all others are irregular. Polygons with all interior angles less than 180° are convex; if a polygon has at least one interior angle greater than 180°, it is concave.
Simple polygons do not cross their sides; complex polygons have self-intersecting sides. Polygons are all around you!