Midsegment of a Triangle (Definition, Theorem, Formula, & Examples)

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

What is midsegment of a triangle?

The midsegment of a triangle is a line constructed by connecting the midpoints of any two sides of the triangle. In any triangle, right, isosceles, or equilateral, all three sides of a triangle can be bisected (cut in two), with the point equidistant from either vertex being the midpoint of that side.

In △ASH, below, sides AS and AH are 24 cm and 36 cm, respectively. Since we know the side lengths, we know that Point C, the midpoint of side AS, is exactly 12 cm from either end. Point R, on AH, is exactly 18 cm from either end.

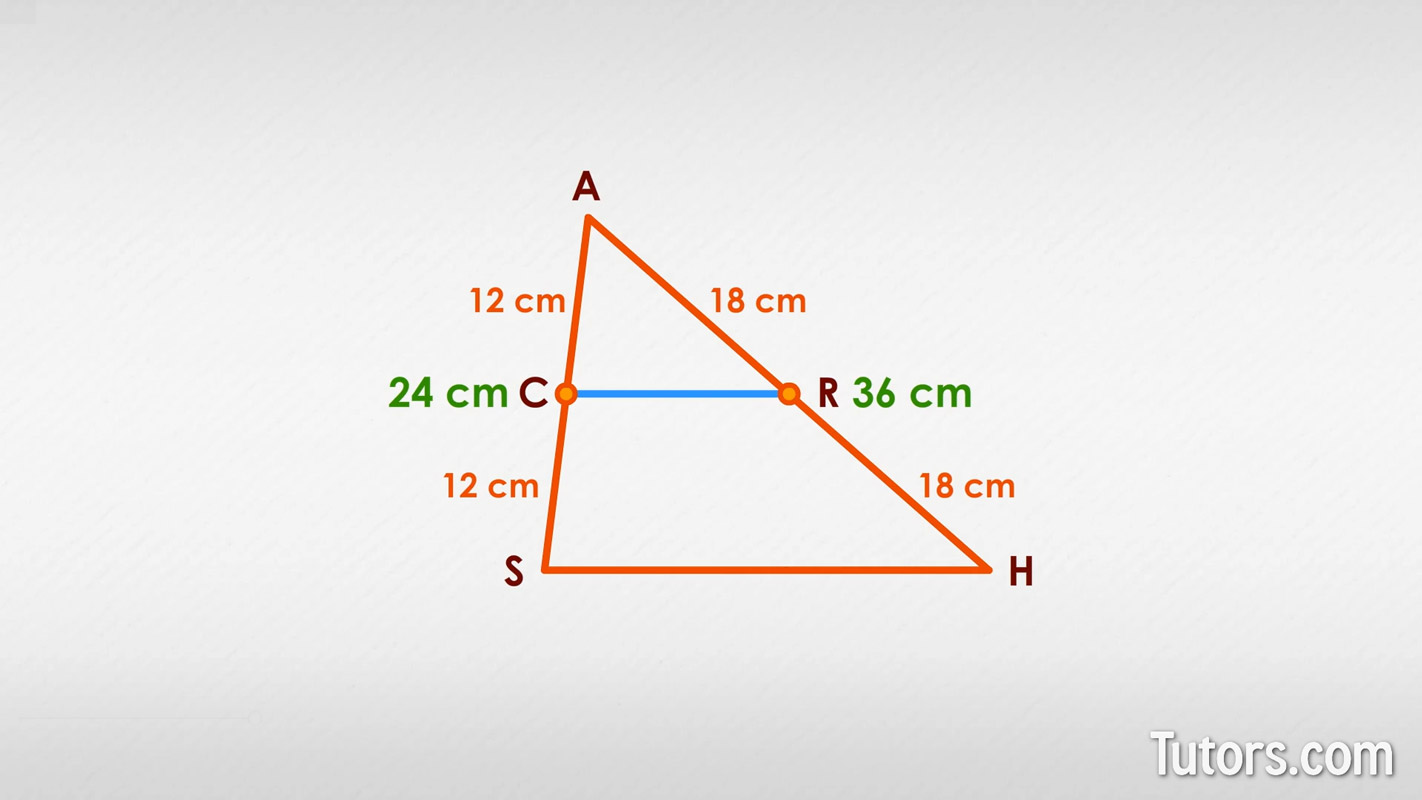
Connecting the midpoints of the sides, Points C and R, on △ASH does something besides make our whole figure CRASH. It creates a midsegment, CR, that has five amazing features.

Five properties of the midsegment

Since triangles have three sides, they can have three midsegments. You can join any two sides at their midpoints. One midsegment is one-half the length of the base (the third side not involved in the creation of the midsegment). That is only one interesting feature. It also:

• Is always parallel to the third side of the triangle; the base

• Forms a smaller triangle that is similar to the original triangle

• The smaller, similar triangle is one-fourth the area of the original triangle

• The smaller, similar triangle has one-half the perimeter of the original triangle

Because the smaller triangle created by the midsegment is similar to the original triangle, the corresponding angles of the two triangles are identical; the corresponding interior angles of each triangle have the same measurements.

Of the five attributes of a midsegment, the two most important are wrapped up in the Midsegment Theorem, a statement that has been mathematically proven (so you do not have to prove it again; you can benefit from it to save yourself time and work).

Triangle Midsegment Theorem

The Triangle Midsegment Theorem tells us that a midsegment is one-half the length of the third side (the base), and it is also parallel to the base.

You don't have to prove the midsegment theorem, but you could prove it using an auxiliary line, congruent triangles, and the properties of a parallelogram.

Midsegment Formula

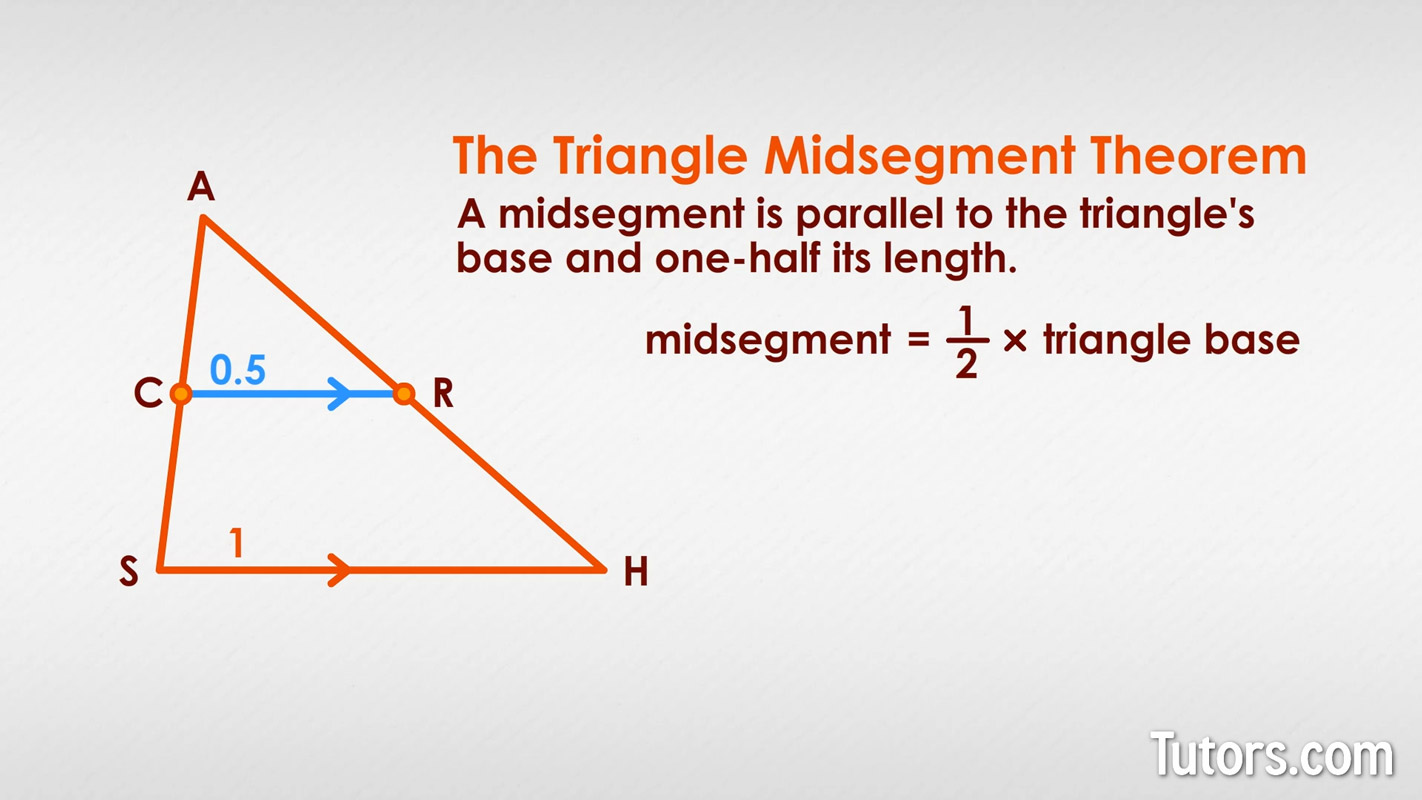
This is powerful stuff; for the mere cost of drawing a single line segment, you can create a similar triangle with an area four times smaller than the original, a perimeter two times smaller than the original, and with a base guaranteed to be parallel to the original and only half as long.

How to find the midsegment of a triangle

Draw any triangle, call it triangle ABC. Using a drawing compass, pencil and straightedge, find the midpoints of any two sides of your triangle. You do this in four steps:

1. Adjust the drawing compass to swing an arc greater than half the length of any one side of the triangle

2. Placing the compass needle on each vertex, swing an arc through the triangle's side from both ends, creating two opposing, crossing arcs

3. Connect the points of intersection of both arcs, using the straightedge

4. The point where your straightedge crosses the triangle's side is that side's midpoint)

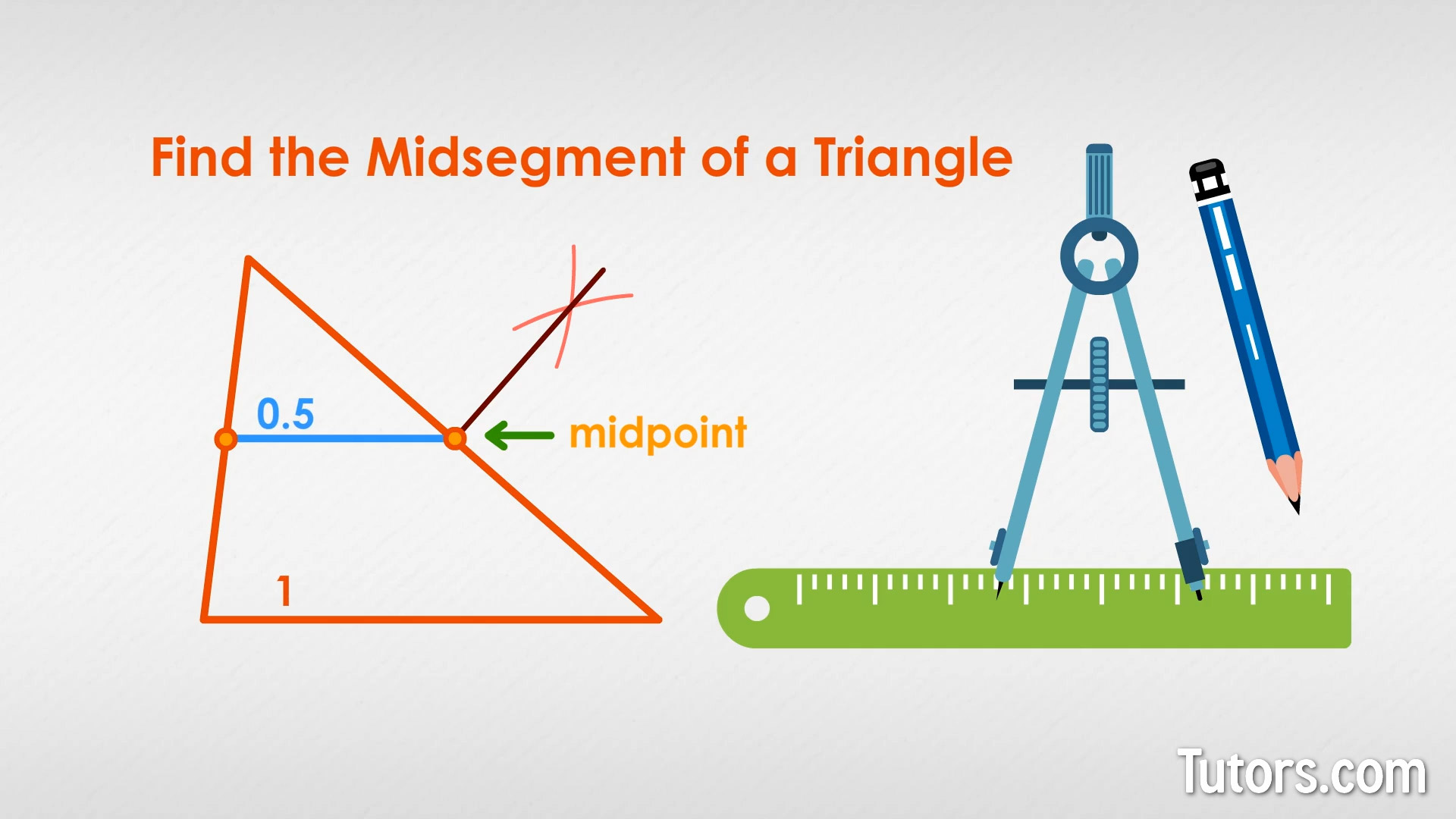
Connect any two midpoints of your sides, and you have the midsegment of the triangle. No matter which midsegment you created, it will be one-half the length of the triangle's base (the side you did not use), and the midsegment and base will be parallel lines!

Triangle midsegment theorem examples

Here is right △DOG, with side DO 46 inches and side DG 38.6 inches. Side OG (which will be the base) is 25 inches. The triangle's area is $482.5i{n}^{2}$.

Which points will you connect to create a midsegment?

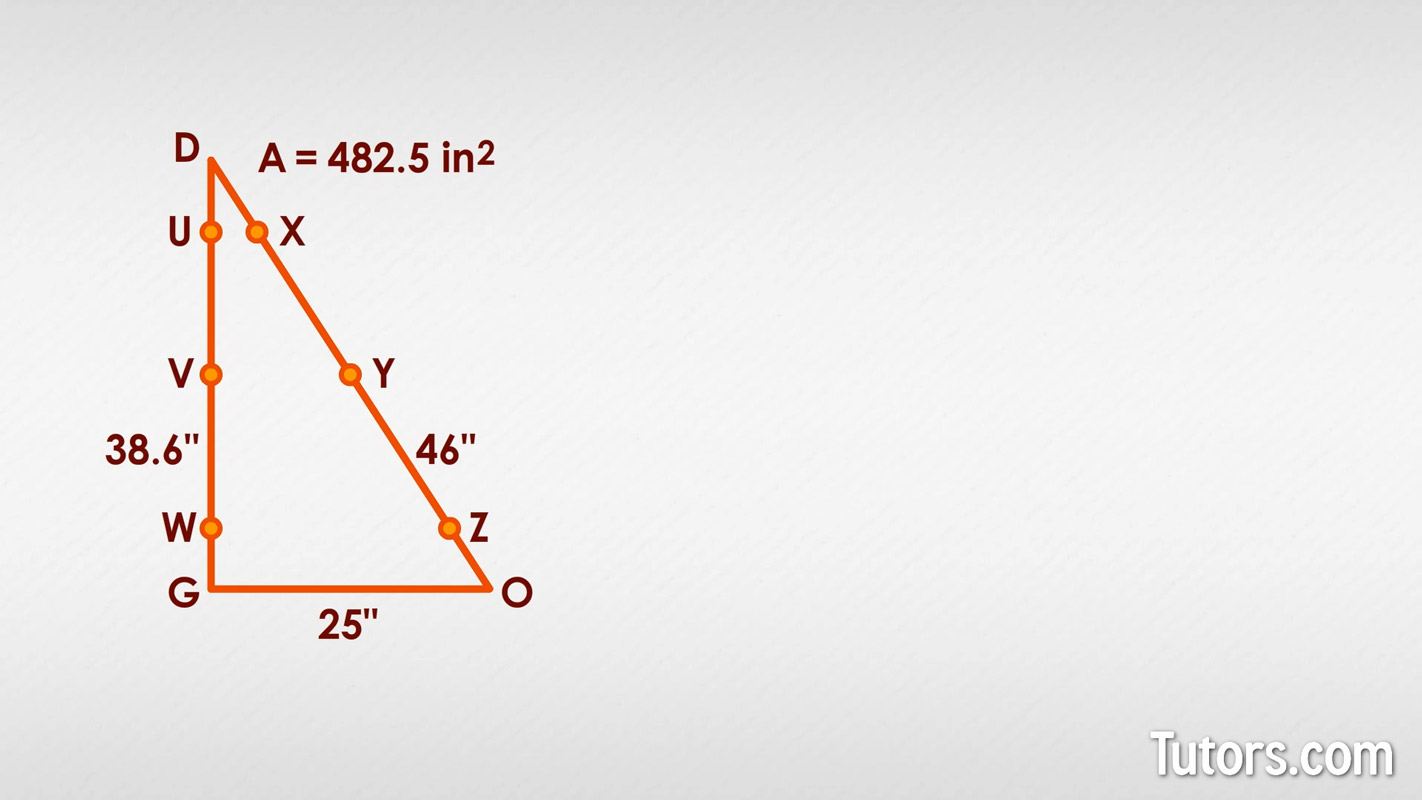
Only by connecting Points V and Y can you create the midsegment for the triangle. That will make side OG the base.

You should be able to answer all these questions:

1. What is the perimeter of the original △DOG?

2. What is the length of midsegment VY?

3. What is the length of side DV?

4. What is the length of side DY?

5. What is the perimeter of the newly created, similar △DVY?

6. What is the area of newly created △DVY?

Here are our answers:

1. Add the lengths: 46" + 38.6" + 25" = 109.6"

2. Midsegment VY = 12.5"

3. Side DV = 23"

4. Side DY = 19.3"

5. Perimeter of △DVY = 54.8"

6. Area of △DVY = $120.625i{n}^{2}$

Sierpinski triangle

Using the midsegment theorem, you can construct a figure used in fractal geometry, a Sierpinski Triangle. The steps are easy while the results are visually pleasing:

1. Draw the three midsegments for any triangle, though equilateral triangles work very well

2. Either ignore or color in the large, central triangle and focus on the three identically sized triangles remaining

3. For each corner triangle, connect the three new midsegments

4. Again ignore (or color in) each of their central triangles and focus on the corner triangles

5. For each of those corner triangles, connect the three new midsegments

This continuous regression will produce a visually powerful, fractal figure: