How to Find the Angle of a Triangle
Angles in a triangle
A triangle is the simplest possible polygon. It is a two-dimensional (flat) shape with three straight sides forming an interior, closed space. It has three interior angles. One of the earliest concepts to learn in geometry is that triangles have interior angles adding up to 180°. But how do you know? How can you prove this is true? Let's find out!
How to find the angle of a triangle
You may have a triangle where only two angles have been labelled and measured. Now that you are certain all triangles have interior angles adding to 180°, you can quickly calculate the missing measurement. You can do this one of two ways:
Subtract the two known angles from 180°.
Plug the two angles into the formula and use algebra: a+b+c=180°
How to find the missing angle of a triangle
Two known angles of a triangle are 37° and 24°. What is the missing angle?
We can use two different methods to find our missing angle:
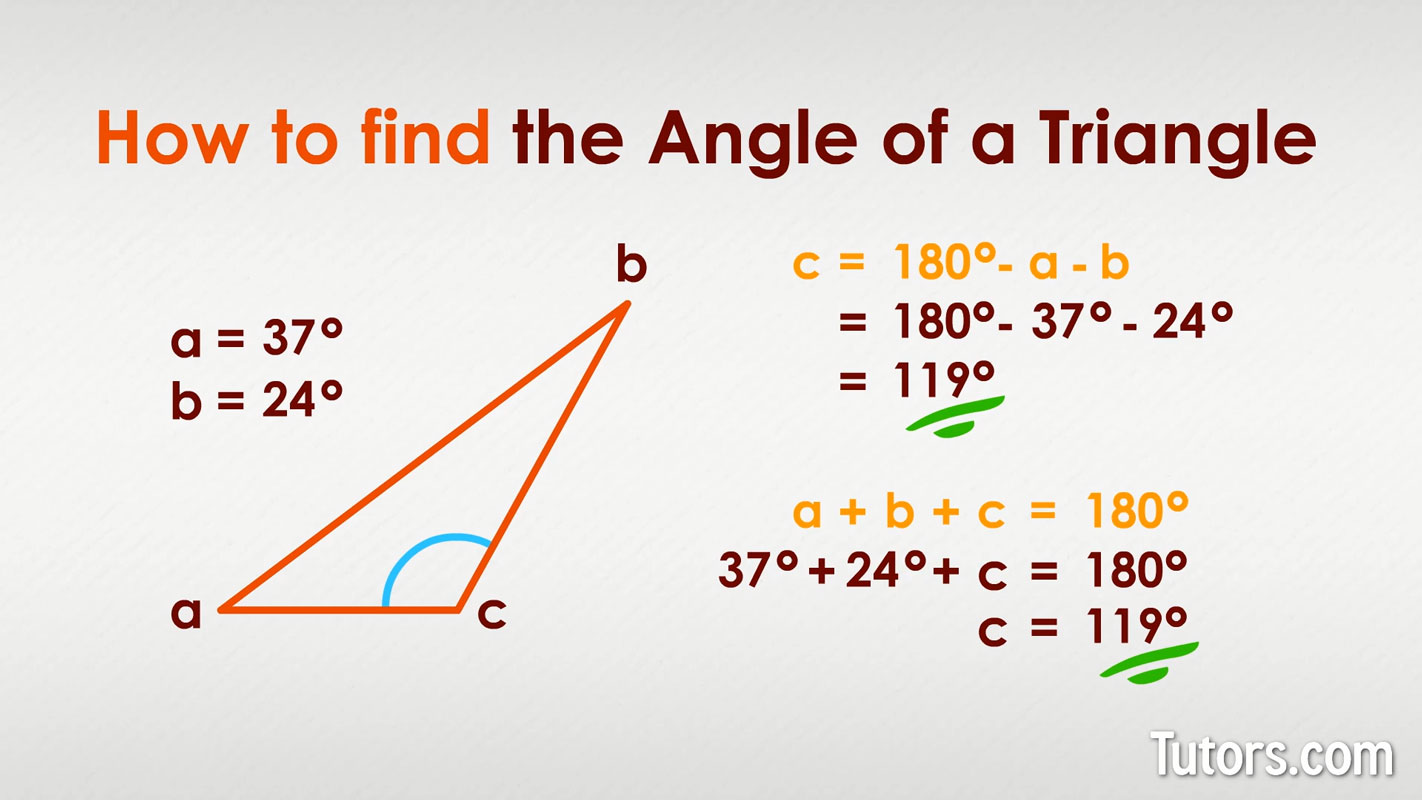
Subtract the two known angles from 180°:
Plug the two angles into the formula and use algebra: a + b + c = 180°
Triangle angle formula
Let's draw a triangle and label its interior angles with three letters a, b, and c. Our sample will have side ac horizontal at the bottom and ∠b at the top.
Now that we've labeled our angles, we have a formula we can refer to for the angles. It is a + b + c = 180°, which tells us that if we add up all of our angles, they will always equal 180.
Now, let's draw a line parallel to side ac that passes through Point b (which is also where you find ∠b).
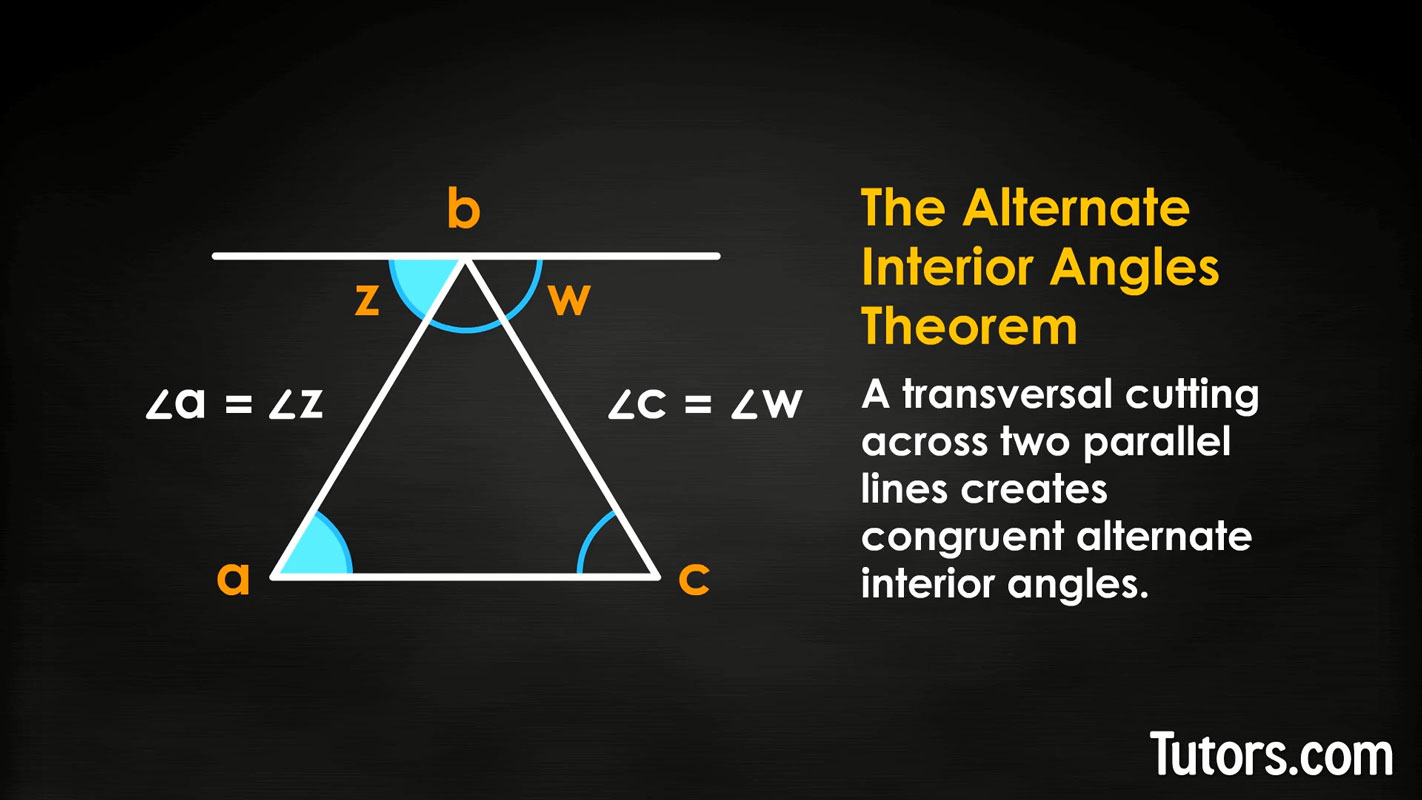
That new parallel line created two new angles on either side of ∠b. We will label these two angles ∠z and ∠w from left to right. Side ab of our triangle can now be viewed as a transversal, a line cutting across the two parallel lines.
Alternate interior angles theorem
By the alternate interior angles theorem, we know that ∠a is congruent (equal) to ∠z, and ∠c is congruent to ∠w.
Did we lose you? Do not despair! The Alternate Interior Angles Theorem tells us that a transversal cutting across two parallel lines creates congruent alternate interior angles. Alternate interior angles lie between the parallel lines, on opposite sides of the transversal. In our example, ∠a and ∠z are alternate interior angles, and so are ∠c and ∠w.
We now have the three angles of our triangle carefully redrawn and sharing Point b as a common vertex. We have ∠z as a stand-in for ∠a, then ∠b, and finally ∠w as a stand-in for ∠c. And look, they form a straight line!
A straight line measures 180°. This is the same type of proof as the parallel lines proof. The three angles of any triangle always add up to 180°, or a straight line.
Triangle angle sum theorem
Our formula for this is a + b + c = 180° where a, b, and c are the interior angles of any triangle.
Angles in a triangle sum to 180° proof
You need four things to do this amazing mathematics trick. You need a straightedge, scissors, paper, and pencil. Draw a neat, large triangle on a piece of paper. Any triangle – scalene, isosceles, equilateral, acute, obtuse – whatever you like.
Label the inside corners (the vertices that form interior angles) with three letters, like R−A−T. Cut the triangle out, leaving a little border around it so you can still see all three edges
Now tear off the three corners of your triangle. Do not use the scissors, because you want jagged edges, which help you avoid confusing them with the straight sides you drew. You will have three smaller triangular bits, each with an interior angle labelled R, A, or T. Each little piece has two neat sides and a rough edge.
You will also have a rough hexagon that is the leftover part of the original, larger triangle.
Take your three little labelled corners and arrange them together so the rough-cut edges are all away from you. The only way to do that is to make them line up, to form a straight line. The three interior angles, RAT, have added up to make a straight angle, also called a straight line.
There; you did it!
Lesson summary
If you carefully studied this lesson, you now are able to identify and label the three interior angles of any triangle, and you can recall that the interior angles of all triangles add to
What you learned:
With this video and lesson, you learned to:
Identify and label the three interior angles of any triangle
Recall that the interior angles of all triangles add to 180°
Demonstrate a proof of the sum of interior angles of triangles
Apply a formula for the sum of interior angles of any triangle
Calculate the missing measurement of any interior angle of any triangle
180°. You can also demonstrate a proof of the sum of interior angles of triangles and apply a formula, a + b + c = 180°, where a, b, and c are the interior angles of the triangle. Further, you can calculate the missing measurement of any interior angle of any triangle using two different methods.