Heron's Formula
What is Heron's formula?
Think of what a great thinker you would have to have been for people to remember your name more than 19 centuries after you lived. Heron of Alexandria was an inhabitant of Alexandria at a time when the Romans ruled the city.
His name is connected to a formula for finding the area of any triangle if you only know the lengths of their sides. The formula, still bearing his name all these centuries later, is known as either Heron's Formula or Hero's Formula.

Heron's formula
To see Heron's Formula at work, you need a triangle. Construct one by drawing any three intersecting line segments. Each side will be labeled a, b, and c.
The distance completely around the triangle -- its perimeter -- is the sum of a + b + c. The semiperimeter of the triangle is half the perimeter. We will label the semiperimeter s.
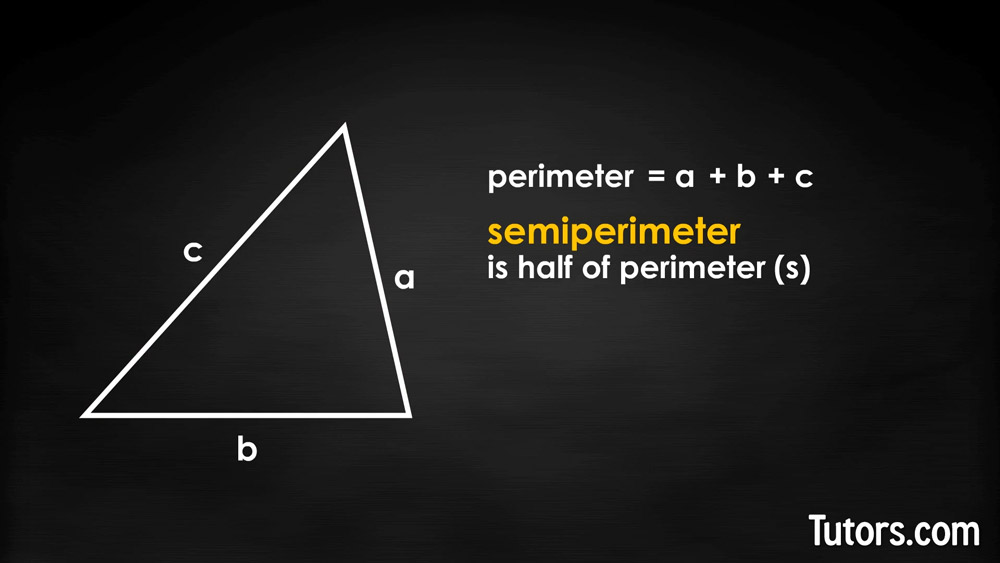
No need to worry about angles; no need to know the height! Using Heron's Formula, we only need the lengths of the sides.
And now, from across the sands of time, here is Heron's Formula for finding area (A) of any triangle if you know the lengths of sides a, b, and c and the semiperimeter s:
Solve the mathematics inside the parentheses first, so you will subtract the length of each side from the semiperimeter.
Then multiply all three of those answers, and then multiply by the semiperimeter.
After that, you take the square root of that answer.
Semiperimeter
Some people find the concept of half the perimeter of a polygon to be a little … well, weird. But semiperimeter -- half the perimeter -- is very useful, and for Heron's Formula, you need it!
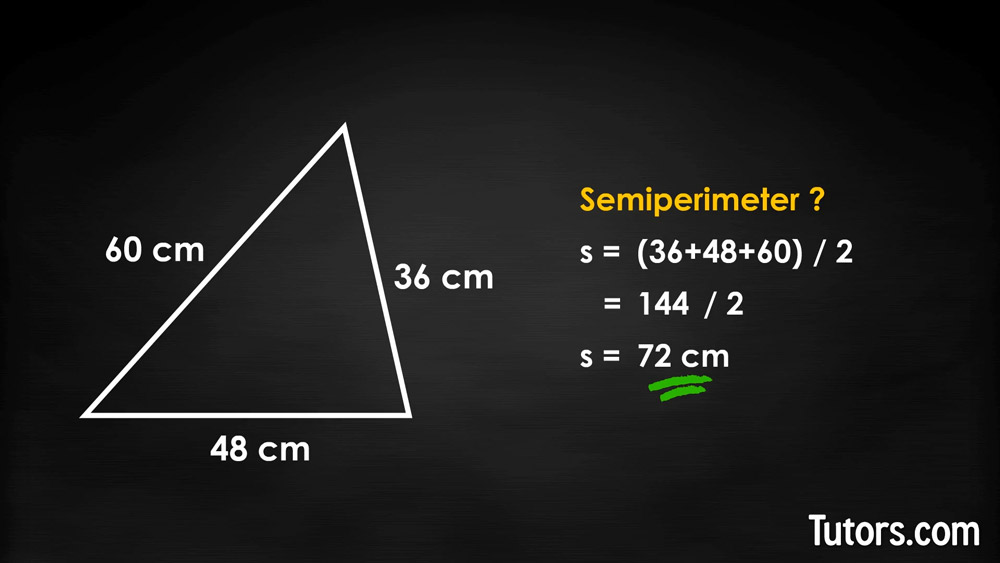
Finding the semiperimeter s is a two-step process: add up the length of the three sides first, and then divide by 2.
Let's try it. You have a triangle with sides of 3, 4, and 5 feet.
Another example
Try one on your own. The triangle has sides of 36, 48, and 60 centimeters. What is its semiperimeter?
A word about square roots
You may not have encountered square roots in your mathematics excursions before. A square root is a number that gives you a specific answer when multiplied times itself.
Suppose you want to know the square root of 49; what number, times itself, will give you 49?
The answer is 7. So, sqrt 49 = 7.

Usually the square root of a number does not come up so neatly. Just going to a neighboring number from our example, 49, shows this. The square root of 50 is 7.07106781187.
Sometimes your answer using Heron's Formula will give an answer to many decimal places. Usually, you round your answer to a specific number of decimal places to reach a specific level of accuracy.
The answer you get using Heron's Formula is, of course, expressed in square units of whatever the linear units were.
When to use Heron's area formula
In most cases, you calculate the area of a triangle by taking the base times the height. You do not always know the triangle's height, however. The base is one of the triangle's sides, so if you know the lengths of the other two sides, you have enough information to plug your three lengths into Heron's Formula:
Try it
Let's go back to our example triangle with sides of 3, 4 and 5 feet (sides a, b, and c). We already calculated the semiperimeter above where s = 6.

Plug all those numbers into Heron's Formula:
Heron's formula proof
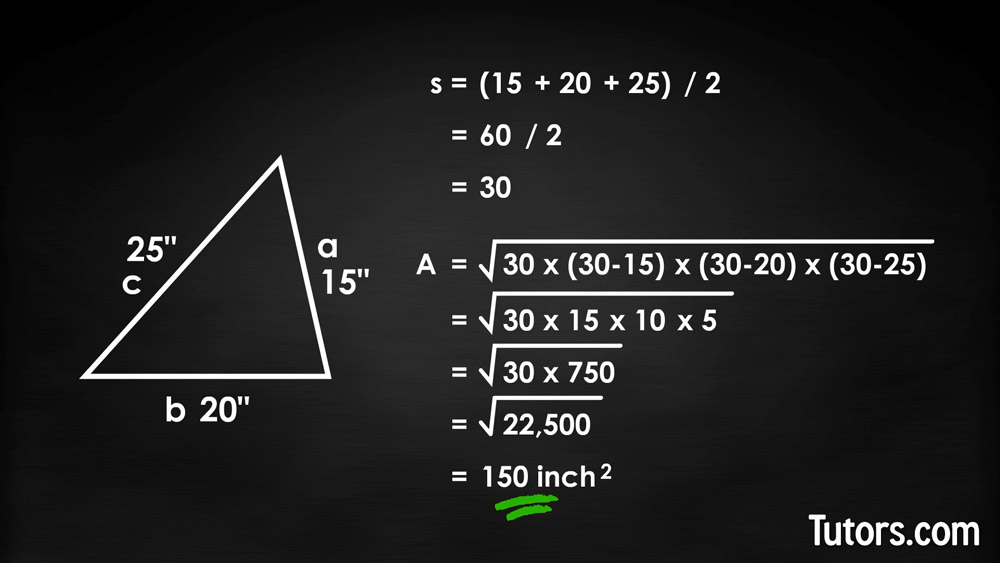
For your first attempt on your own, we will use small values to make your multiplying easier. Imagine a triangle with sides 15, 20 and 25 (a, b, and c) inches long. Start by calculating the triangle's semiperimeter:
Now put sides a, b, and c, together with semiperimeter (s), 30", into Heron's Formula:
Ready for a harder example?
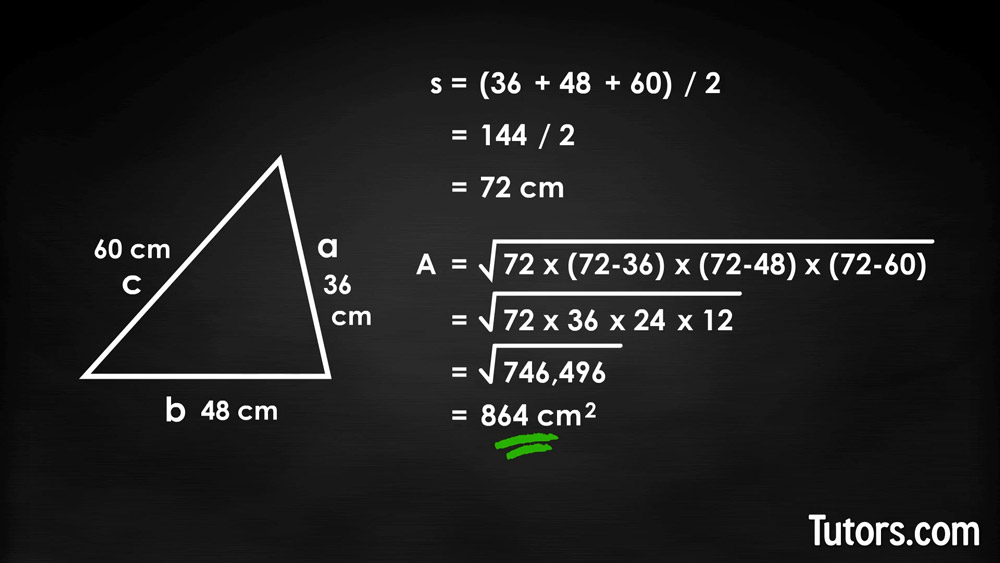
Use the other triangle from our examples, with sides of 36, 48, and 60 centimeters (a, b, c). First, let's calculate the semiperimeter:
Plug all those numbers into Heron's formula:
Lesson summary
By watching the video and reading this lesson, you now can calculate area of a triangle if you know the lengths of the triangle's sides, recognize reasons to use Heron's Formula, apply knowledge of square roots to solving a problem, and use Heron's Formula to calculate the area of a triangle.