Dodecagon — Sides, Area & Angles

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

What is a dodecagon?

A dodecagon is a type of polygon with these properties:

1. It has two dimensions

2. It has 12 straight sides enclosing a space

3. It has 12 interior angles

Sometime during the mid 1600s, a mathematician felt the need for a descriptive word for a 12-sided polygon. The word dodecagon comes from the Greek, dōdeka-, which means 12, and + -gōnon, which means angled.

Dodecagons can be regular, meaning all interior angles and sides are equal in measure. They can also be irregular, with varying angles and sides of different measurements. If you ever try to draw a dodecagon freehand, you will no doubt make an irregular dodecagon.

Finding angles and perimeter of a regular dodecagon

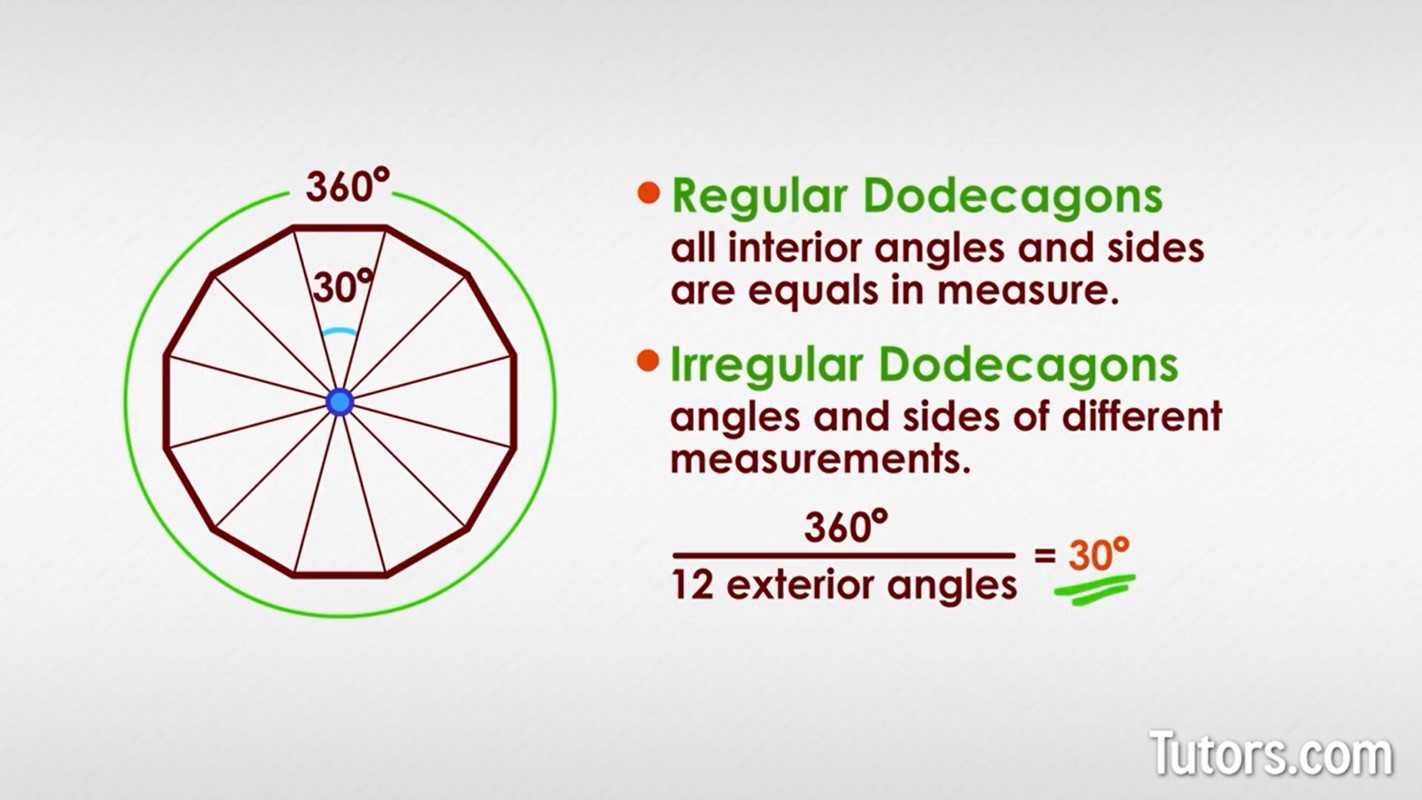
No matter the shape, a regular polygon can have its exterior angles add to no more than 360°. Think: to go around the shape, you make a complete circle: 360°.

So, divide 360° by the dodecagon's twelve exterior angles. Each exterior angle is 30°.

That was the easy part. The interior angles of a dodecagon are a bit harder. You can use this generic formula to find the sum of the interior angles for an n-sided polygon (regular or irregular):

• Sum of interior angles = $(n-2)\times 180°$

• Sum of interior angles = $10\times 180°=1800°$

Once you know the sum, you can divide that by 12 to get the measure of each interior angle:

This means each side intersects the next side only 30° less than a straight line! That is one of two reasons drawing a regular dodecagon freehand is so difficult. The other reason is the difficulty of drawing 12 equal-length sides.

To calculate the perimeter of a regular dodecagon, multiply one side's measurement, s, times 12:

• Perimeter = $12\times s$

• Length of one side: 17 mm

• Perimeter: $12\times 17mm=204mm$

Area of a regular dodecagon

The easy calculations are behind us. Now let's tackle area of a regular dodecagon. For a regular dodecagon with sides s, the area formula is:

As an example, the 2017 British one-pound coin is a regular dodecagon. One side of this beautiful coin is 6.278 mm in length. What is the area of this coin?

• $A=3\times {s}^{2}\times (2+\sqrt{3})$

• $A=3\times (6.278mm{)}^{2}\times (2+\sqrt{3})$

• $A=118.239852m{m}^{2}\times 3.73205080757$

• $A=441.277135143m{m}^{2}$

• $A=4.41277c{m}^{2}$

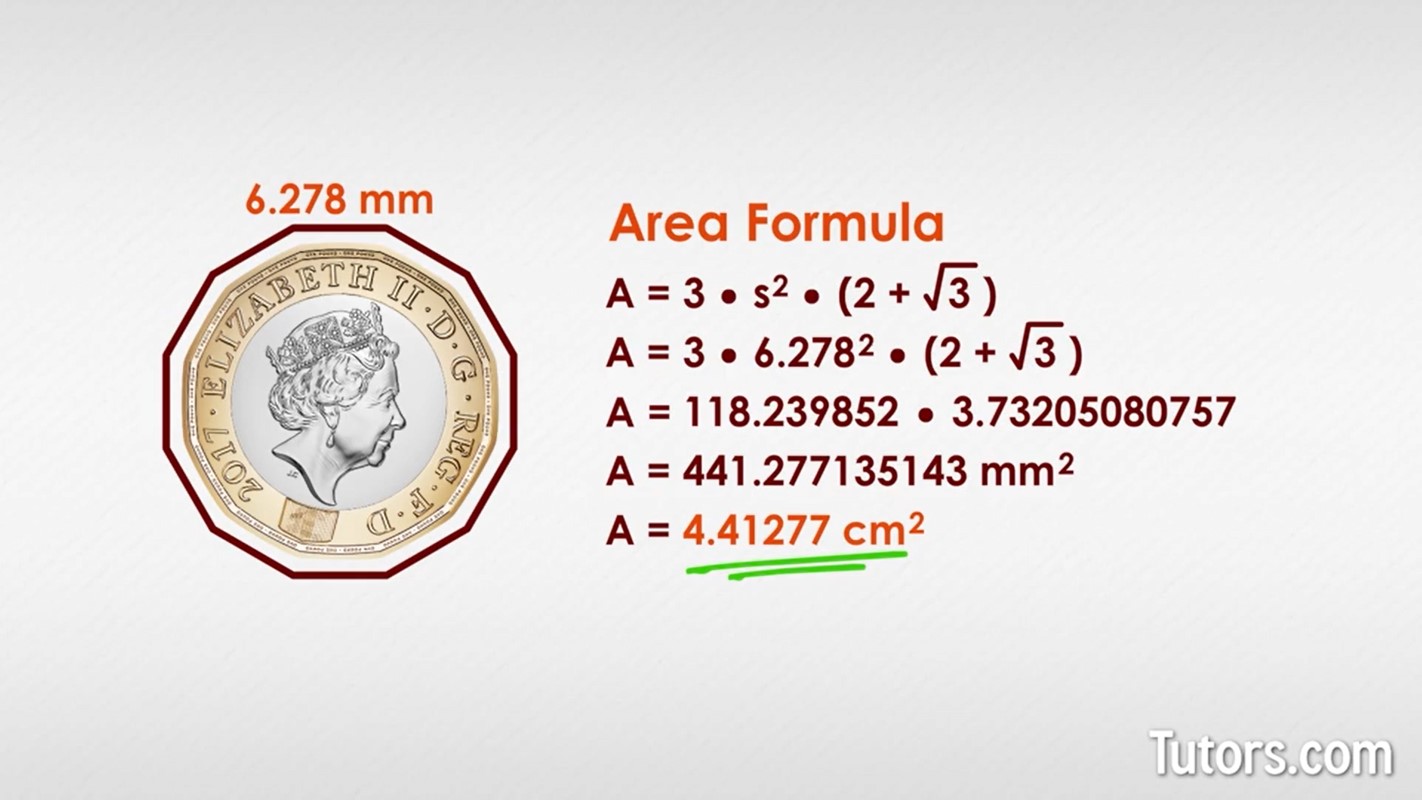
You will seldom need that level of precision with your decimal places, so feel free to round as you wish; $441.277m{m}^{2}$ is very precise.

Working with dodecagons

You can draw a regular dodecagon with only a pencil, paper, compass and straightedge, but the steps are a bit involved.

You will find few if any examples of naturally occurring dodecagons in the natural world, but coin minters like the shape. It is very hard to counterfeit. One online coin catalog lists some 449 dodecagonal coins of many different nations.

Besides the British coin, Australia, Fiji and the Solomon Islands mint dodecagonal coins.

Try it!

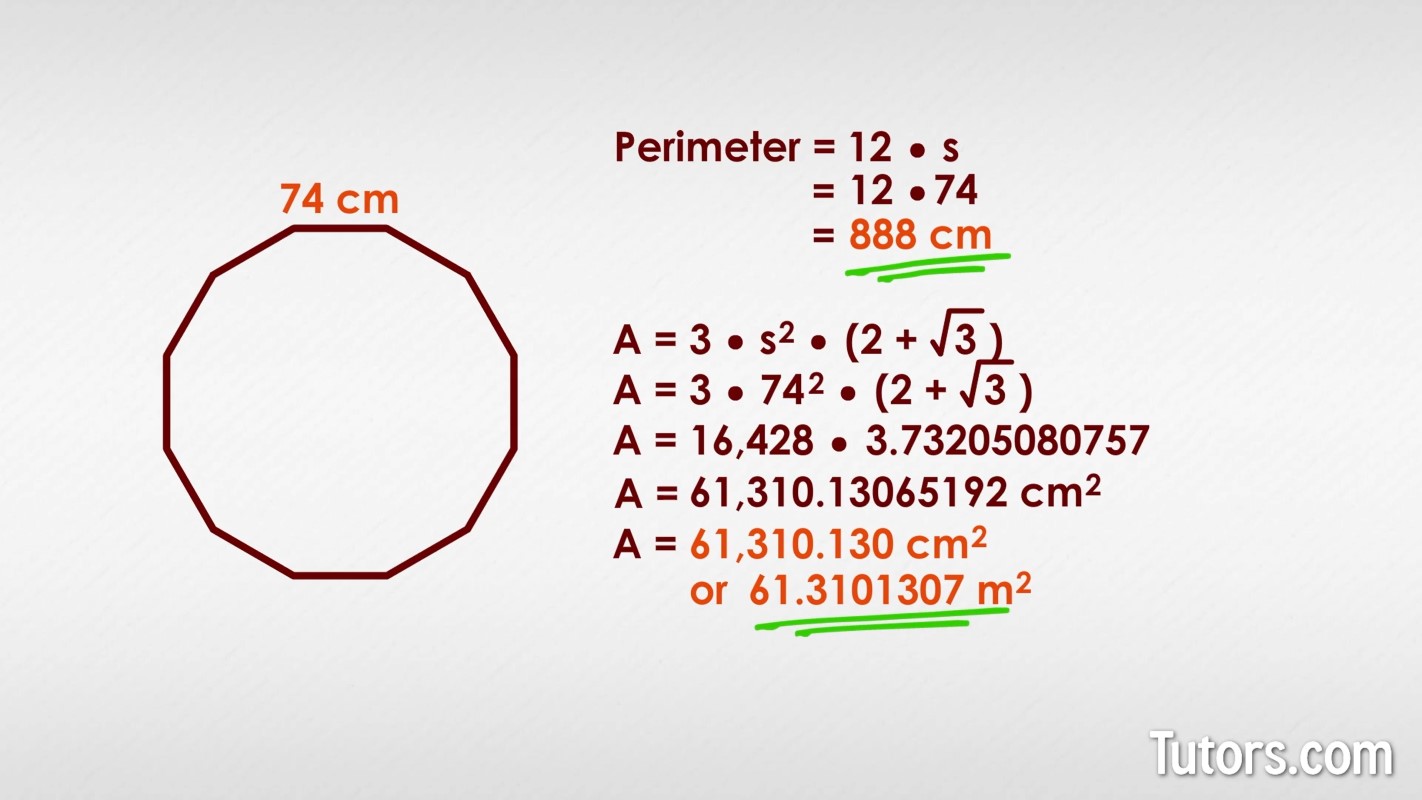
Here is a regular dodecagon with sides measuring 74 cm. What is its perimeter and area?

Think before you peek!

Perimeter:

• Perimeter = $12\times s$

• Length of one side: 74 cm

• Perimeter: $12\times 74cm=888cm$

Area:

• $A=3\times {s}^{2}\times (2+\sqrt{3})$

• $A=3\times (74cm{)}^{2}\times (2+\sqrt{3})$

• $A=\mathrm{16,428}c{m}^{2}\times 3.73205080757$

• $A=\mathrm{61,310.13065192}c{m}^{2}$

• $A=6.13101307{m}^{2}$