What is a Line Segment? (Definition, Distance Formula, Example)

Line segment

A line segment is a portion or piece of a line that allows you to build polygons, determine slopes, and make calculations. Its length is finite and is determined by its two endpoints.

The line segment is a snippet of the line. No matter how long the line segment is, it is finite.

Line segment symbol

You name a line segment by its two endpoints. The shorthand for a line segment is to write the line segments two endpoints and draw a dash above them, like $\overline{CX}$:

What is a line?

The definition of a line is the set of points between and beyond two points. A line is infinite in length. All points on a line are collinear points.

Straight line symbol

In geometry, the straight line symbol is a line segment with two arrowheads at its ends, like $\overleftrightarrow{CX}$. You identify it with two named points, indicated by capital letters. Pick a point on the line and give it a letter, then pick a second; now you have the name of your line:

Rays

A ray is a part of a line that has one endpoint and goes on infinitely in only one direction. You cannot measure the length of a ray.

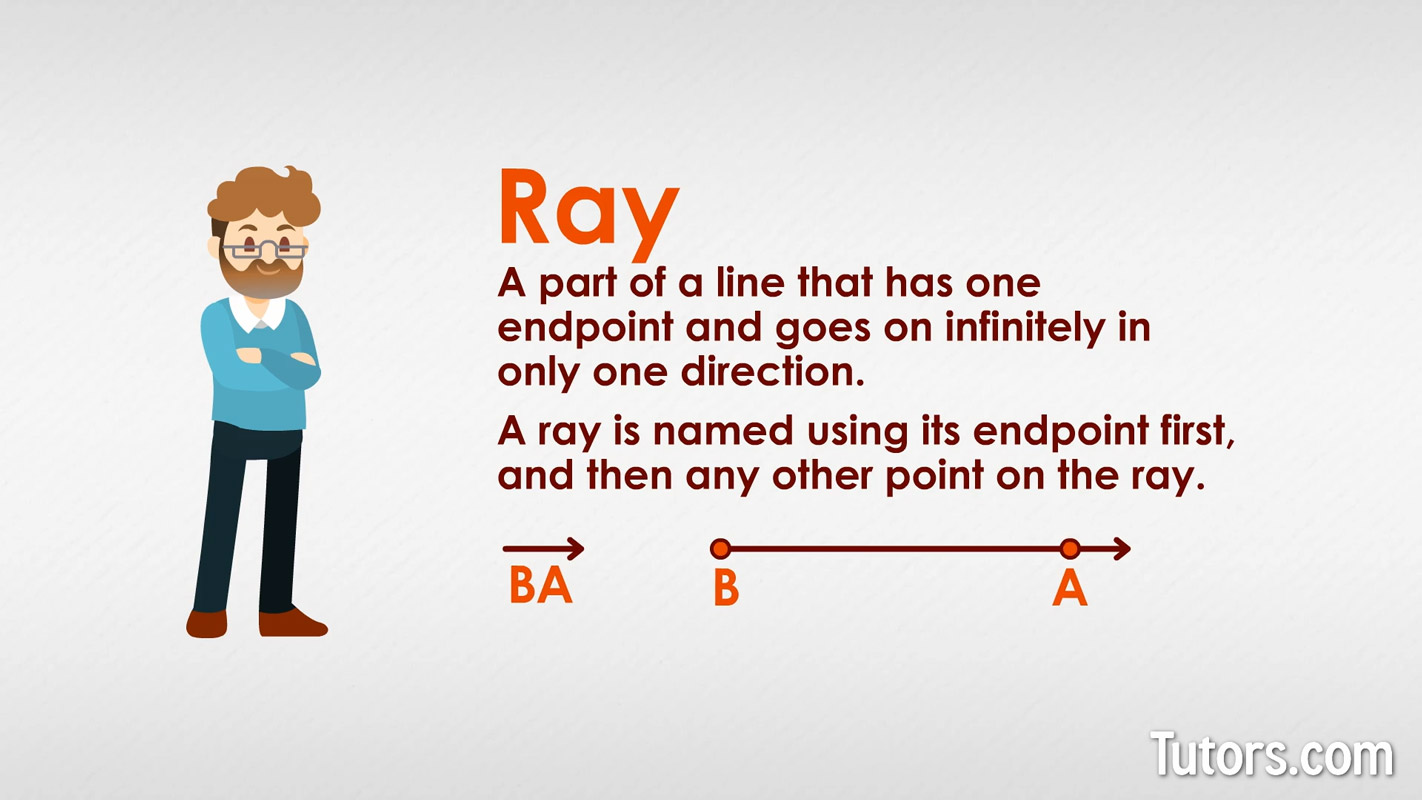
A ray is named using its endpoint first, and then any other point on the ray. In this example, we have Point B and Point A ($\overset{\to }{BA}$).

Measuring line segments

A line segment is named by its endpoints, but other points along its length can be named, too. Each portion of the line segment can be labeled for length, so you can add them up to determine the total length of the line segment.

Line segment example

Here we have line segment $\overline{CX}$, but we have added two points along the way, Point G and Point R:

To determine the total length of a line segment, you add each segment of the line segment. The formula for the line segment CX would be: CG + GR + RX = CX

• 7 units line segment CG

• 5 units line segment GR

• 3 units line segment RX

That's a total of 15 units of length for $\overline{CX}$.

Coordinate plane

A coordinate plane, also called a Cartesian plane (thank you, René Descartes!), is the grid built up from a x-axis and a y-axis. You can think of it as two perpendicular number lines, or as a map of the territory occupied by line segments.

To determine the length of horizontal or vertical line segments on the plane, count the individual units from endpoint to endpoint:

To determine the length of line segment $\overline{LM}$, we start at Point L and count to our right five units, ending at Point M. You can also subtract the x-values: 

. For vertical lines, you would subtract y-values.

When working in or across Quadrants II, III and IV, recall that subtracting a negative number really means adding a positive number.

How to find the length of a diagonal line segment on a coordinate plane

Use the Pythagorean Theorem to calculate line segment lengths of diagonals on coordinate planes. Recall that the Pythagorean Theorem is ${a}^{2}+{b}^{2}={c}^{2}$ for any right triangle.

A diagonal on a coordinate grid forms the hypotenuse of a right triangle, so can quickly count the units of the two sides:

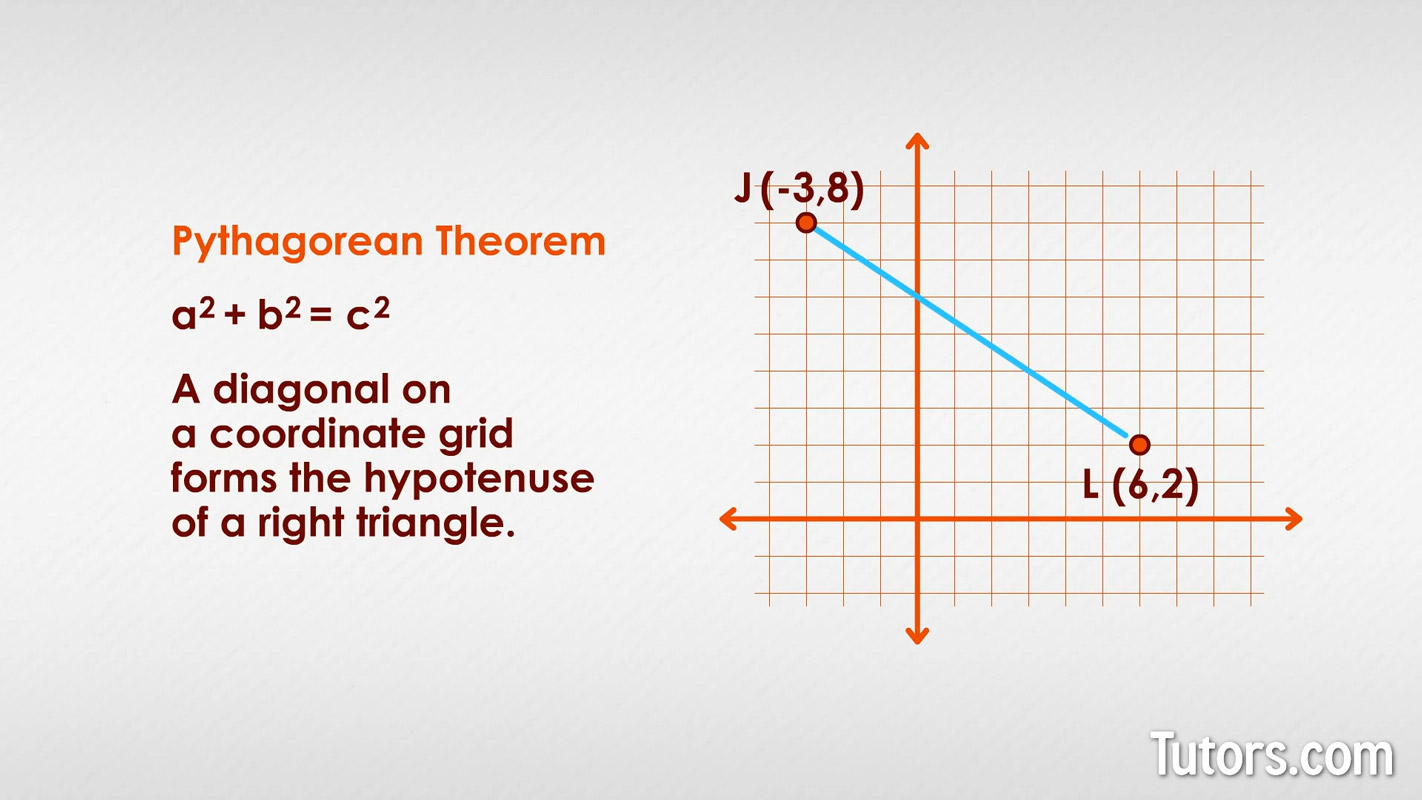
Count units straight down from Point J to the x-value 2 (which lines up with Point L):

So, line segment $\overline{JK}=6$

Count units straight across from Point K to Point L:

So, line segment $\overline{KL}=9$. Now we have ${6}^{2}+{9}^{2}={c}^{2}$:

The length of line segment

is approximately $10.816 units$.

The distance formula

A special case of the Pythagorean Theorem is the Distance Formula, used exclusively in coordinate geometry. You can plug in the two endpoint x- and y- values of a diagonal line and determine its length. The formula looks like this:

To use the distance formula, take the squares of the change in x-value and the change in y-value and add them, then take that sum's square root.

The expression $({x}_{2}-{x}_{1})$ is read as the change in x and $({y}_{2}-{y}_{1})$ is the change in y.

Imagine we have a diagonal line stretching from Point P (6, 9) to Point I (-2, 3), and you want to measure the distance between the two points.

The distance formula makes this an easy calculation:

Using the Distance Formula, we find that line segment $\overline{PI}=10units$.

Examples of line segments in real life

Real-world examples of line segments are a pencil, a baseball bat, the cord to your cell phone charger, the edge of a table, etc. Think of a real-life quadrilateral, like a chessboard; it is made of four line segments. Unlike line segments, examples of line segments in real life are endless.