Similar Figures — Definition, Examples, Proportions & Solving
Similar figures definition
If two flat shapes are the same, but one is larger or smaller than the other, they are said to be similar figures.
An easy way to test similarity is to consider transformations that could make one into the other:
Enlarge or shrink
Flip
Rotate
Notice anything about these two pictures of an Australian wombat? The pictures are of the same cute little animal, but the picture on the right is smaller in both dimensions (width and length). The pictures are not identical, but they are similar. In mathematics, similar figures have the same shape, ratios and proportions, but not the same dimensions.

All that is needed is to rotate the second wombat and enlarge him to match the first wombat.
If you can enlarge or shrink one shape and it will exactly match the other, the two shapes are similar, even if you further have to flip or rotate a shape to make two shapes correspond, they are similar.
Most mathematicians consider congruent shapes to also be similar (going beyond similarity to be identical in size). Yet you must keep in mind that, though congruent shapes are automatically similar, similar shapes are not automatically congruent.
Similar figures proportions and ratios
Similar figures reveal themselves mathematically when we study their dimensions. Take two right triangles, one with its two sides sides 4 meters and 6 meters long, and the other with sides 8 meters and 12 meters long:
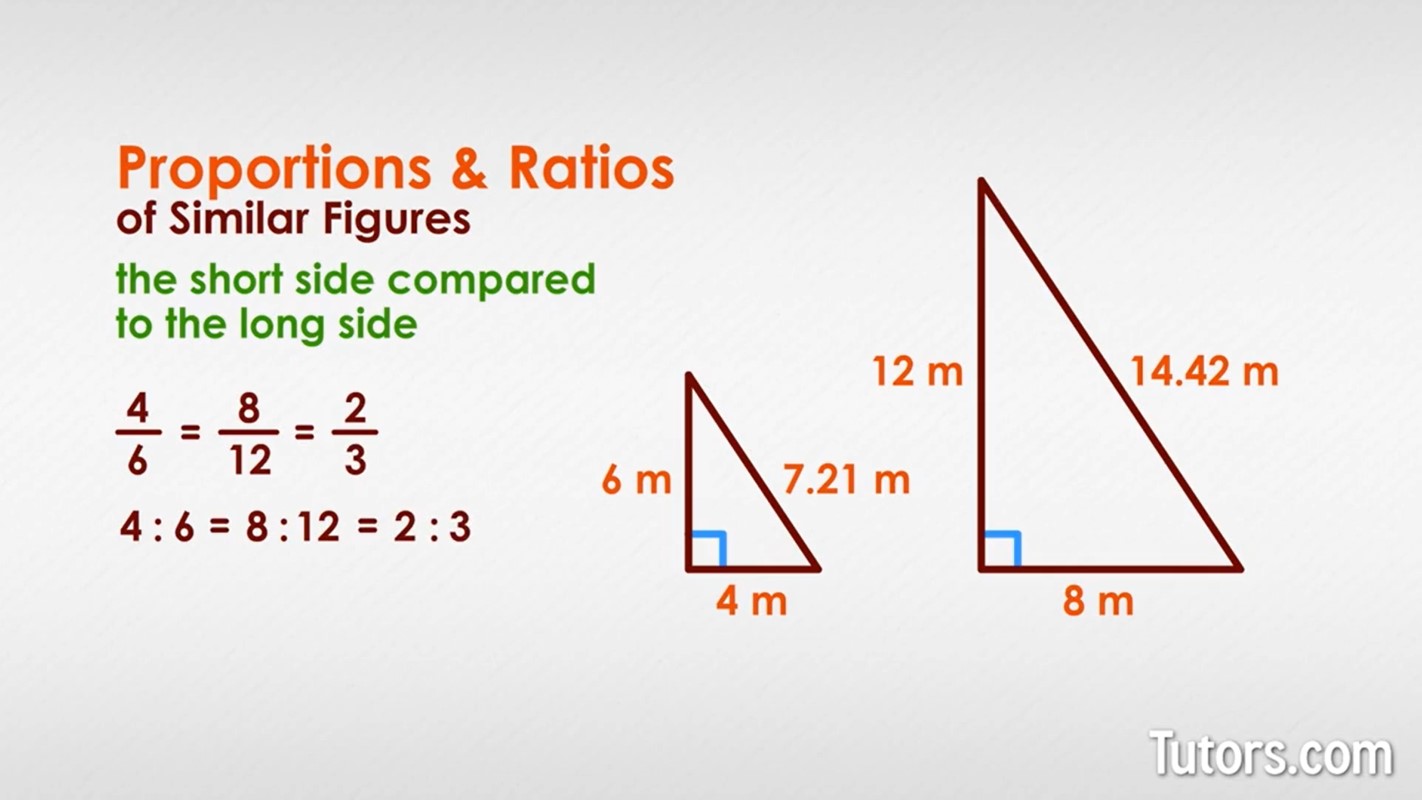
If we were to set up ratios of the two triangles' two sides, in which the short side is compared to the long side, we would see a pattern. We take the smaller triangle's short side, 4 meters, and set it in a ratio to the long side, 6 meters. Repeat for the larger triangle's short and long sides, either as a fraction or as a ratio:
Clearly the relationship, , between short and long sides holds for both triangles.
You can even compare ratios between the two figures. Take the two short sides and compare them to the two long sides, again either as a fraction or a ratio:
The ratios of the triangles are the same. We can use the third side, the hypotenuse, to confirm this ratio. When we compare hypotenuses we get the same relationship:
All those relationships simplify to , which means these two triangles are in proportion to each other, with one exactly half the size of the other (or, if you wish, one twice the size of the other). We could cut out the little one and hold it closer to our eyes, and it would exactly cover the larger one.
All polygons can have similar pairs. Two triangles, two squares, two pentagons. You just cannot say a right triangle is similar to, say, a square.
How to solve similar figures
Not all similar figures are as easy as wombats or triangles. Take these two rhombuses, for example:
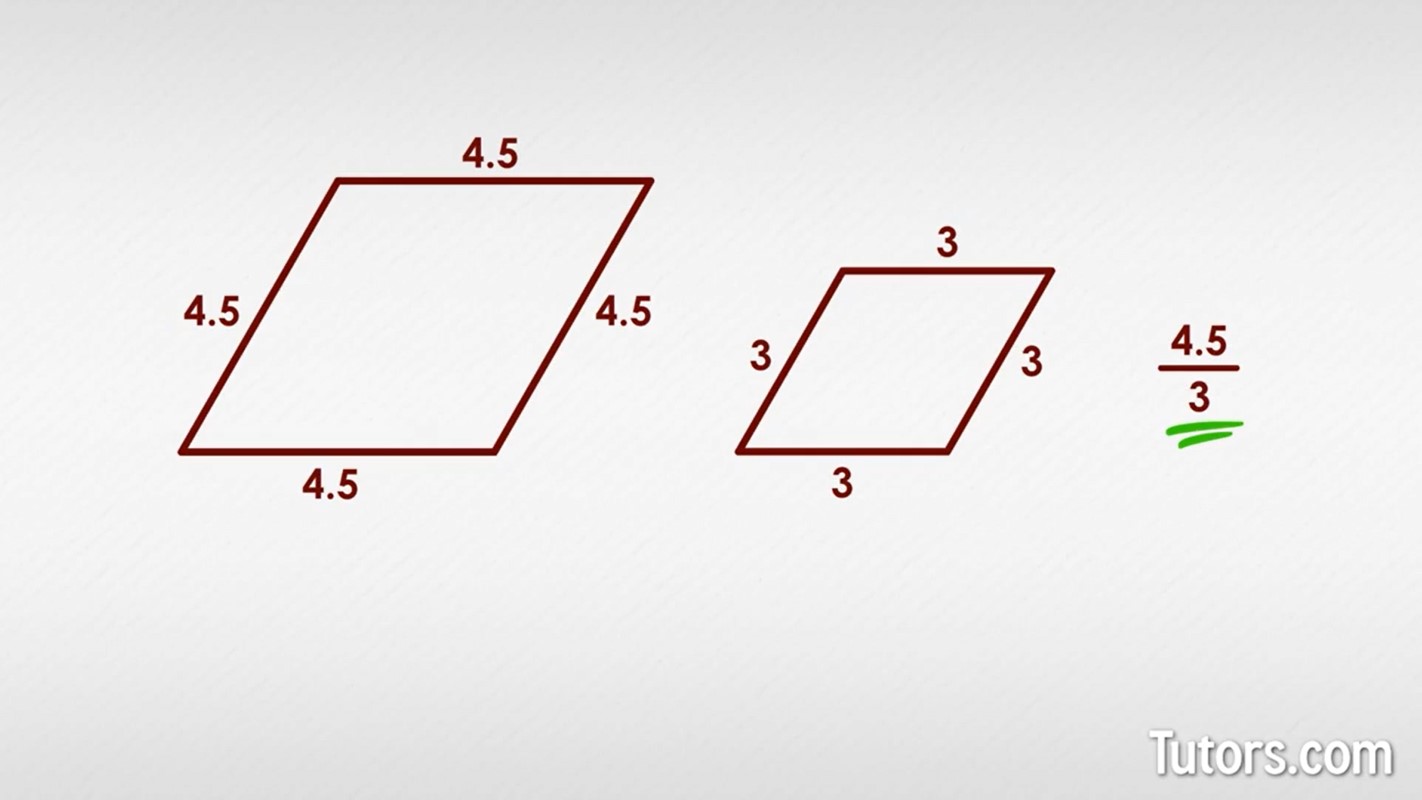
Take any one side of the first rhombus, and compare it to the other rhombus.
No matter where you look, these two rhombuses have the same ratio of corresponding sides. You can do this for any two polygons.
If you are given angle measurements, use them: angles of similar figures must be congruent. Only the sides are in proportion to each other. The angles are always congruent.
Here are two pentagons that should be familiar to anyone who rounds the bases:
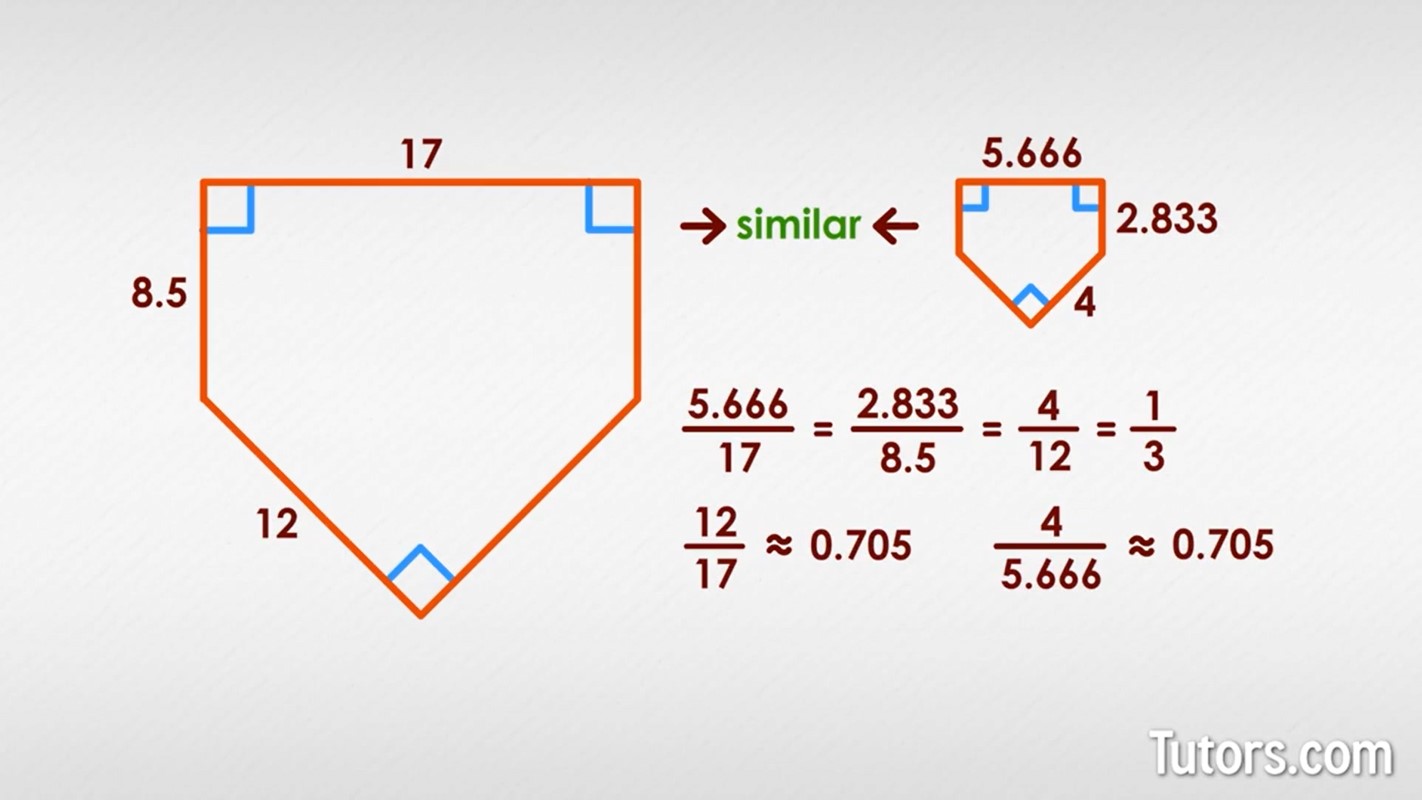
Are these two home plates similar? You can compare the ratios of any corresponding sides:
All three ratios are the same, one-third, so the two figures are similar. Not certain yet? Compare ratios between the figures. Use, say, the diagonal and the top as a ratio:
If those two ratios are equal, then the figures are similar.
They are approximately equal to each other (due to decimal rounding), which means the home plates are similar.
Similar figures examples
Understanding how similar figures work, and seeing relationships between similar figures, can help you in both geometry and real-world applications. The most common way to use similar figures is ages old: knowing the size of a small figure can help you estimate the size of a larger, unknown measurement.
You notice your basketball-playing buddy is exactly 2 meters tall. On this particular sunny day, his shadow is 1 meter long. He is standing next to a Eucalyptus tree, the type native to Australia (home of our wombats) that casts a shadow 10 meters long. How tall is the Eucalyptus tree?
Think of this problem as two similar triangles:
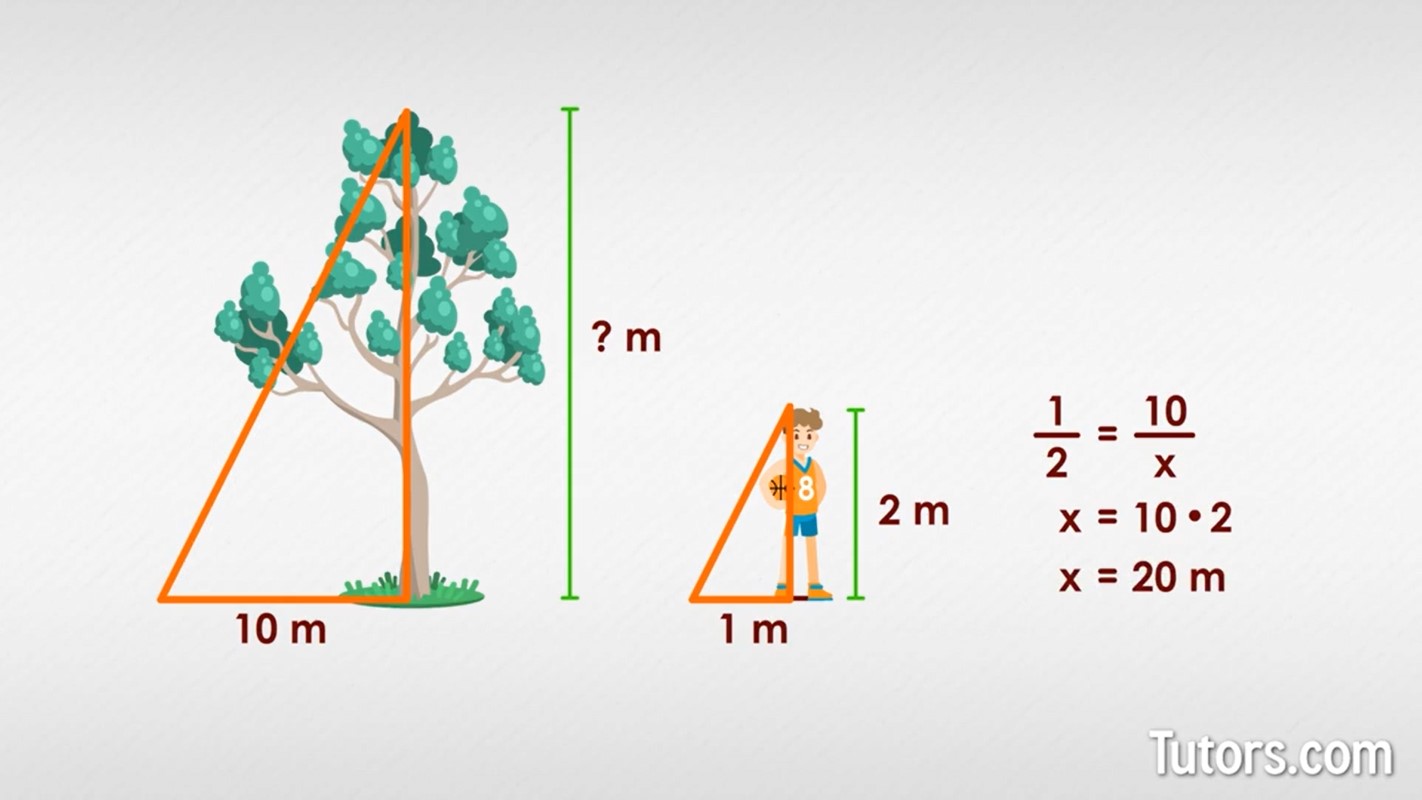
If the two triangles are proportional, they are similar:
The Eucalyptus tree is 20 meters in height.