How To Construct A Perpendicular Bisector
Perpendicular bisector definition
A perpendicular bisector is the line, line segment or ray that bisects a given line segment or side of a polygon at a right angle to that line segment or side of a polygon.
Here we have line segment SH, and we have intersected it at a right angle with ray FI. Note that the distance from endpoint S to the ray FI is equal to the distance from endpoint H to ray FI:
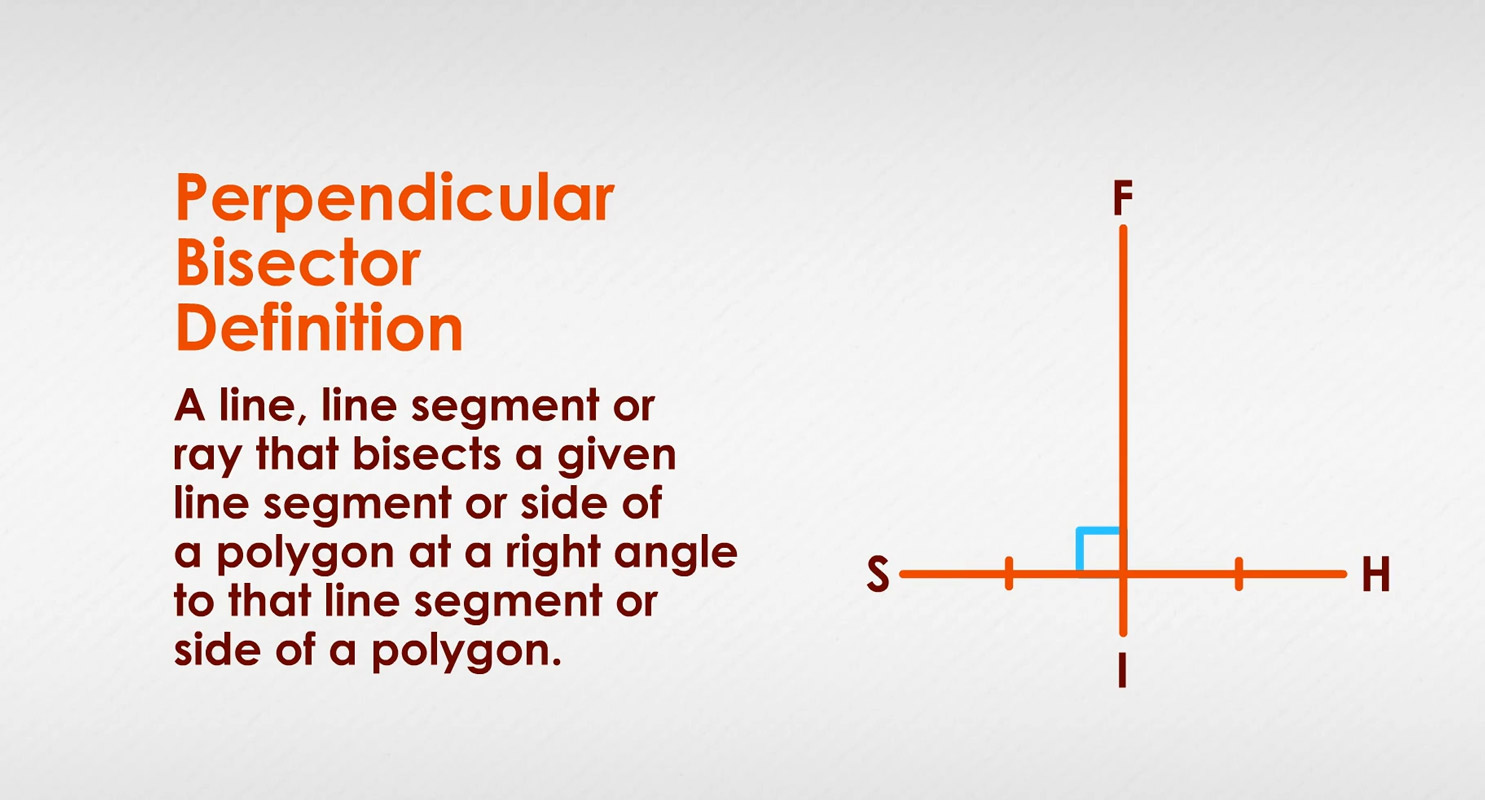
We know that ray FI is perpendicular to SH because of the little square: □. The square indicates a right angle, 90°. We know that the two segments it creates in SH are congruent because of the little tick marks. They show the two segments of line segment SH are equal in measure, or congruent.
What does perpendicular mean?
A line, ray or line segment is perpendicular to a given figure if it is at a right angle, 90°, to that figure. Here is line SL perpendicular to line IM:
What is a bisector?
Anything that cuts another geometric figure into two equal parts is a bisector. Geometry has angle bisectors, line bisectors, and bisectors of the sides of polygons. Diagonals of parallelograms are bisectors of each other. Areas of polygons can be bisected.
A circle can have bisectors (called diameters) that halve the entire circle, bisectors of chords, bisectors of arcs (we will see these later), and bisectors of inscribed angles.
Combining these two concepts of a bisector that is also perpendicular to a constructed line segment or side of a polygon, we get the perpendicular bisector.
How to construct a perpendicular bisector
With only a straightedge, pencil, paper and drawing compass you can create your own perpendicular bisector:
Draw a line segment of any length on a sheet of paper.
Using only your eye (no need to measure!), set your compass to a radius that seems a bit larger than half the line segment's length.
Set the compass needle point on an endpoint of the line segment.
Strike an arc of the compass to go from above the line segment to below it (you do not need to go all the way around).
Without changing the compass legs, repeat on the other endpoint.
Where the two arcs of your circles intersect, those are the endpoints of the perpendicular bisector of your line segment! Really, just connect them carefully and precisely with your straightedge, and you will have bisected the line at a 90° angle.
Perpendicular bisector of a triangle
A perpendicular bisector is useful in constructing triangles (of any size) with exactly two equal-length sides. The perpendicular bisector of a line segment is exactly halfway between the segment's endpoints, so any point on the bisector is equidistant (equally far) from those endpoints, no matter how high above or far below the line segment that point may be.
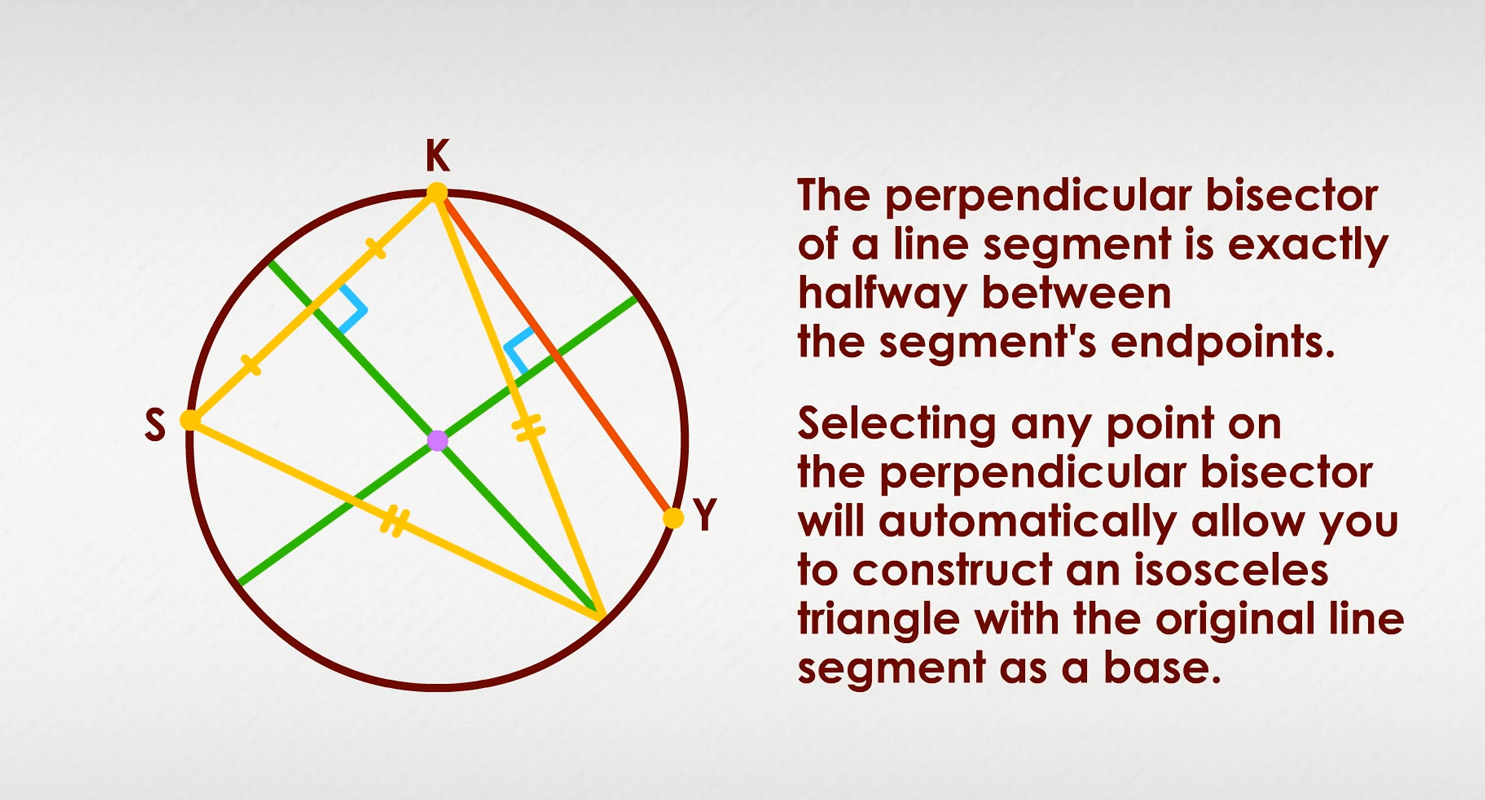
This means selecting any point on the perpendicular bisector will automatically allow you to construct an isosceles triangle with the original line segment as a base. Follow along, again using only a straightedge, drawing compass, pencil and paper:
Construct a line segment EN, of any length. In our example below, we will make it 20 cm long.
As before, use your drawing compass to strike two arcs of circles, one from each endpoint.
Construct a perpendicular bisector that extends at least 20 cm above your original line segment EN.
Label its top endpoint P.
If you connected Point P to E, and P to N, you would have triangle PEN, with sides PE and PN equal, which gives you an isosceles triangle
More, if you pick a point below Point P, anywhere on the perpendicular bisector, connecting that point to the two endpoints of EN will also give you an isosceles triangle! The perpendicular bisector is also the altitude (or height) of the triangle for side EN.
Perpendicular bisector examples
NASA has a plan for a new series of very large rockets, the Space Launch System (SLS). The core stage is a staggering 8.4 meters in diameter and 64.6 meters in height. Without an understanding of the perpendicular bisector definition and application, though, the rocket would never get off the ground.
NASA's SLS lifting stage is huge; 8.4 meters in diameter is approximately the width of a typical high school classroom. Finding the center of that big, empty, curving space is incredibly hard to do without knowledge of a perpendicular bisector. Finding the center is necessary, too, to know where to attach reinforcing pieces that run from one wall of the rocket to the opposite wall, for positioning fuel tanks, and for mounting electronics in the rocket.
A bit higher up the rocket, in a piece called the universal stage adapter, small secondary payloads will tuck in around the circumference of the spacecraft. Here, too, we need the perpendicular bisector to correctly find those little niches.
To find the center of any circle, even when you do not know its diameter, select any three points on the circle, which will form two pairs of points:
Construct a perpendicular bisector using Points S and K, and then construct another perpendicular bisector using Points K and Y:
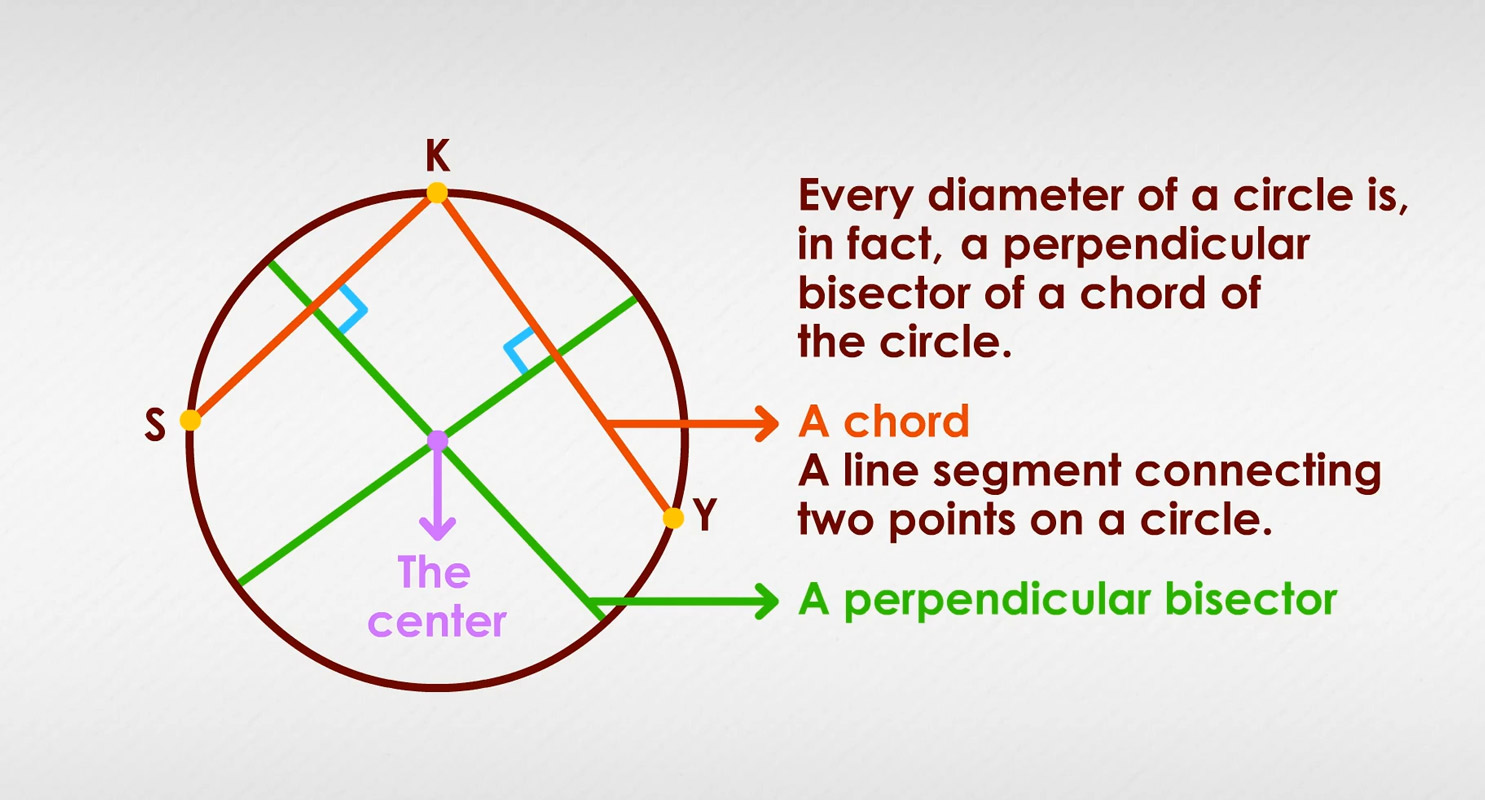
The two perpendicular bisectors will intersect within the circle's arc. The two perpendicular bisectors meet at the circle's center. Once you know the center, you can change your drawing compass to extend from center to circle and get an exact measurement of the circle's radius.
For NASA's universal stage adapter, where the 13 shoebox-sized secondary payloads will ring the adapter's walls, each must be perfectly aligned along a diameter of the circle. Every diameter of a circle is, in fact, a perpendicular bisector of a chord of the circle. A chord is a line segment connecting two points on a circle.
Using the perpendicular bisector in real life
Finding the perpendicular bisector is helpful in other fields, too, like archaeology. Archaeologists seldom dig up perfect, intact pieces of pottery. An archaeologist may unearth only parts of a plate, jug, or pot and have to estimate its diameter.
By carefully plotting three points on the plate's circular rim, the archaeologist can reconstruct the original plate's diameter from the two perpendicular bisectors of the chords of the rim!
Why would this be useful? The archaeologist could then get a rough idea of how much of the original piece has been discovered, and how much may still be in the ground, waiting for the moment when it is brought to light once again.
Lesson summary
Now that you have worked through all the examples and reading, you are able to recall and apply the perpendicular bisector definition and construct a perpendicular bisector using simple tools.
You now can also use the perpendicular bisector definition and construction to form a line segment at a right angle to a given line, to divide a line segment exactly in half, and to find the center of a circle of unknown diameter given three points on the circle.