What Is a Parallelogram?

Table of Contents

1. Parallelogram Definition
2. What Does a Parallelogram Look Like?
3. Diagonals of a Parallelogram
4. Types of Parallelograms
5. Properties of Parallelograms
• Parallelogram Sides
• Parallelogram Angles
6. How To Prove A Parallelogram

Parallelogram Definition

A parallelogram is a flat shape with four straight, connected sides so that opposite sides are congruent and parallel. This means a parallelogram is a plane figure, a closed shape, and a quadrilateral.

You can have almost all of these qualities and still not have a parallelogram. If the four sides do not connect at their endpoints, you do not have a closed shape; no parallelogram! If one side is longer than its opposite side, you do not have parallel sides; no parallelogram! If only one set of opposite sides are congruent, you do not have a parallelogram, you have a trapezoid.

What Does a Parallelogram Look Like?

Take a rectangle and push either its left or ride side so it leans over; you have a parallelogram. A rectangle is a type of parallelogram.

You can draw parallelograms. Use a straightedge (ruler) to draw a horizontal line segment, then draw another identical (congruent) line segment some distance above and to one side of the first one, so they do not line up vertically.

Make sure that second line segment is parallel to (or equidistant from) the first line segment. Connect the endpoints, and you have a parallelogram!

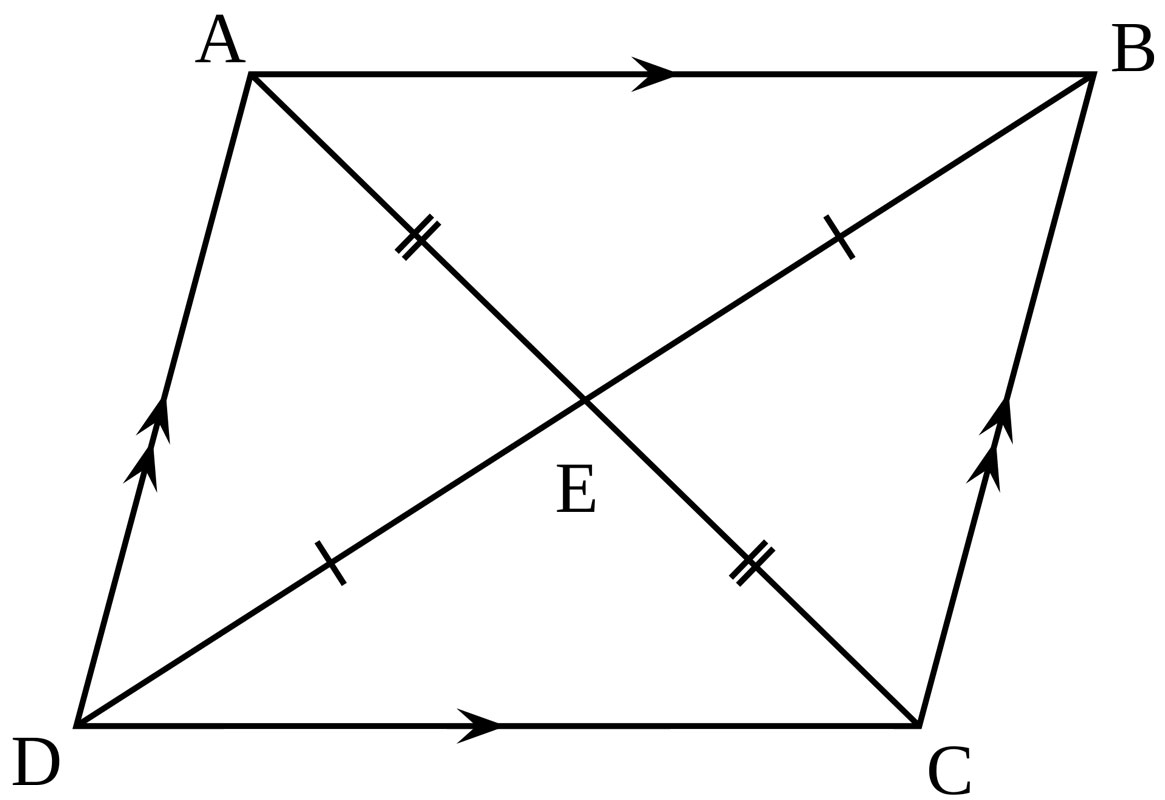
Diagonals of a Parallelogram

Start at any vertex (corner). Write a capital letter, then move either clockwise or counterclockwise to the next vertex. Use a different capital letter. For our parallelogram, we will label it $WXYZ$, but you can use any four letters as long as they are not the same as each other.

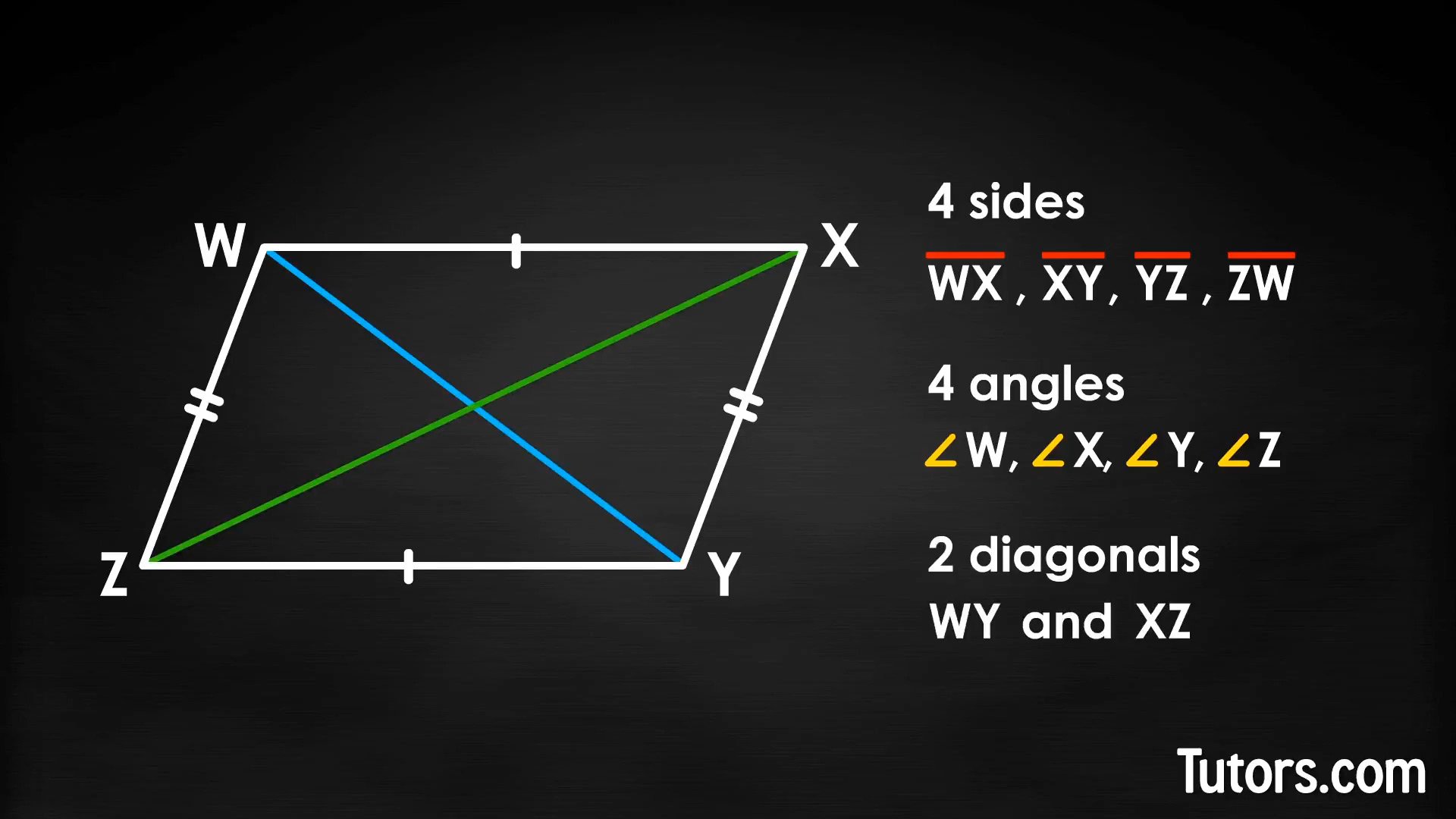
The four line segments making up the parallelogram are $WX$, $XY$, $YZ$, and $ZW$. Notice that line segments $WX$ and $YZ$ are congruent. Line segments $XY$ and $ZW$ are also congruent.

The interior angles are $\angle W$, $\angle X$, $\angle Y$, and $\angle Z$. The opposite angles are congruent. In our parallelogram, that means $\angle W = \angle Y$ and $\angle X = \angle Z$.

Connecting opposite (non-adjacent) vertices gives you diagonals $WY$ and $XZ$. One interesting property of a parallelogram is that its two diagonals bisect each other (cut each other in half). Another property is that each diagonal forms two congruent triangles inside the parallelogram.

Types of Parallelograms

The name "parallelogram" gives away one of its identifying properties: two pairs of parallel, opposite sides.

A parallelogram does not have other names. Other shapes, however, are types of parallelograms. These geometric figures are part of the family of parallelograms:

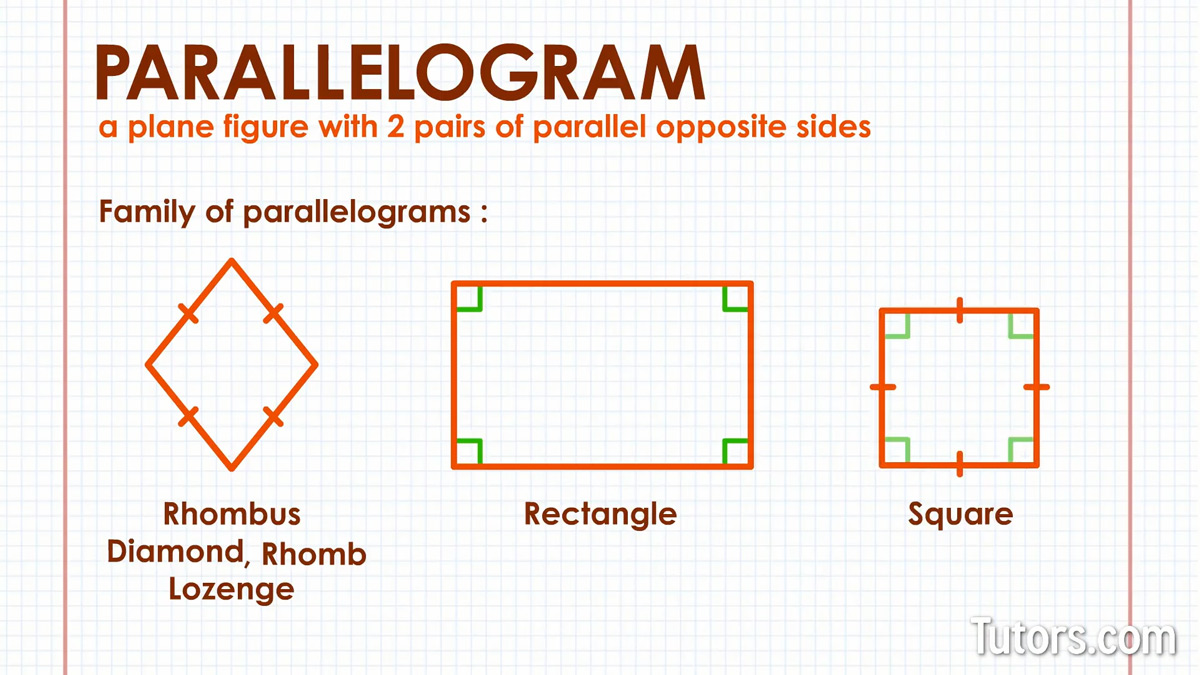
• Rhombus (or diamond, rhomb, or lozenge) -- A parallelogram with four congruent sides
• Rectangle -- A parallelogram with four congruent interior angles
• Square -- A parallelogram with four congruent sides and four congruent interior angles

Properties of Parallelograms

For such simple shapes, parallelograms have some interesting properties. You can examine them based on their diagonals, their sides or their interior angles. We already mentioned that their diagonals bisect each other. Let's look at their sides and angles.

Parallelogram Sides

• Opposite sides are parallel -- Look at the parallelogram in our drawing. The bottom (base) side $YZ$ and top $WX$ are parallel; if you were to extend their line segments, they would never meet. The left and right sides ($XY$ and $ZW$) are also parallel.
• Opposite sides are congruent -- The base side ($YZ$) and the top side ($WX$) of our parallelogram are equal in length (congruent); the left side ($XY$) and right side ($ZW$) are also congruent

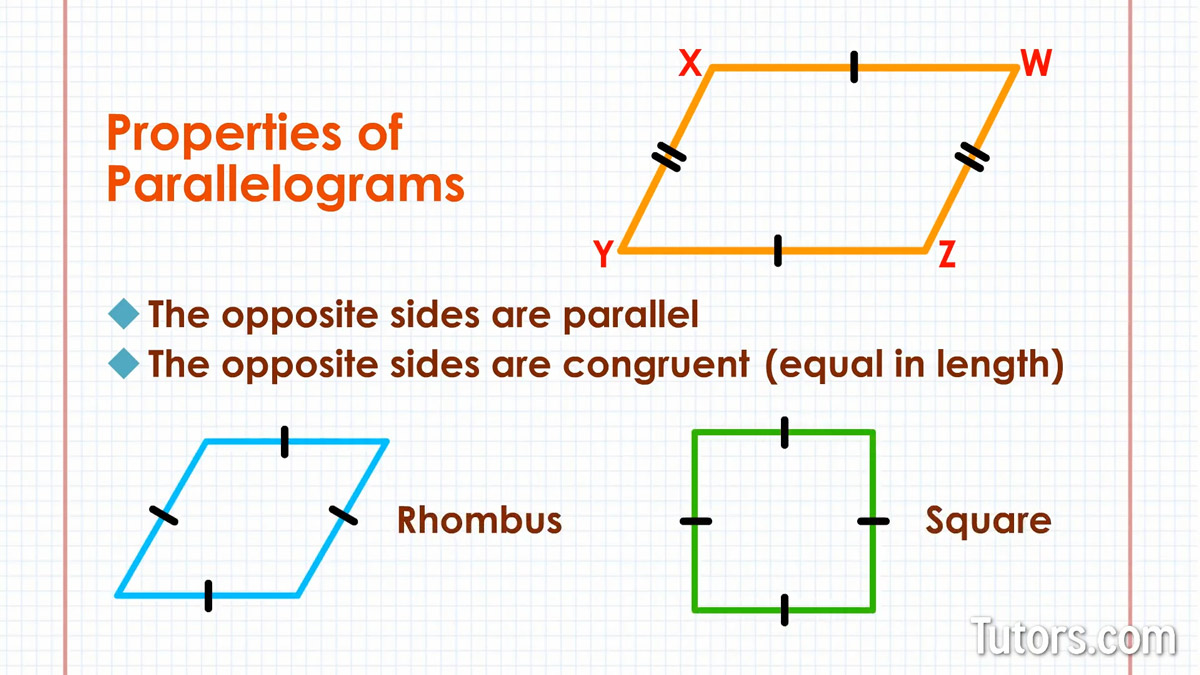
To be a parallelogram, the base and top sides must be parallel and congruent, and so must the left and right sides.

The base and top side make a congruent pair. The left and right side make a congruent pair. The two pairs of congruent sides may be, but do not have to be, congruent to each other.

Parallelogram Angles

Now consider just the interior angles of parallelograms, $\angle W$, $\angle X$, $\angle Y$, and $\angle Z$. As with any quadrilateral, the interior angles add to 360°, but you can also know more about a parallelogram's angles:

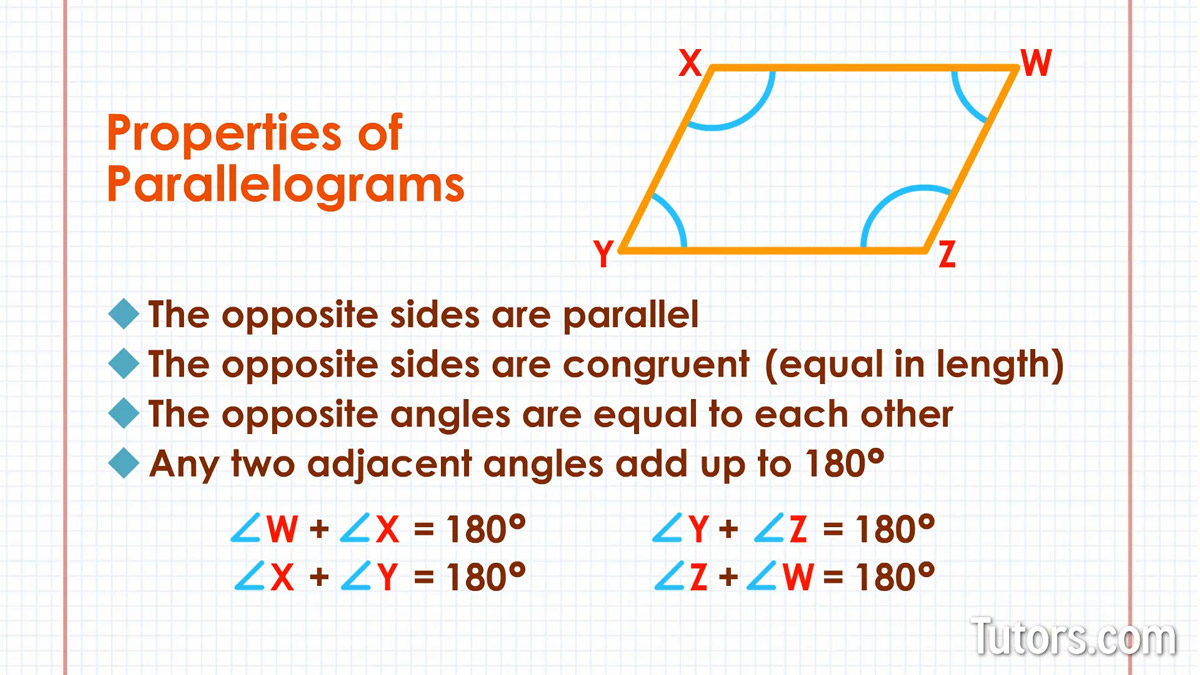
• Opposite angles are equal (congruent) to each other; $\angle W and \angle Y$ are congruent, and $\angle X and \angle Z$ are congruent; the two pairs are not necessarily congruent, but they can be (as in a square or rectangle)
• Any two adjacent angles of a parallelogram add up to $180°$, so you can state four equations:

$\angle W + \angle X = 180°$

$\angle X + \angle Y = 180°$

$\angle Y + \angle Z = 180°$

$\angle Z + \angle W = 180°$

How To Prove A Parallelogram

Using the properties of diagonals, sides, and angles, you can always identify parallelograms. You need not go through all four identifying properties.

Check for any one of these identifying properties:

1. Diagonals bisect each other
2. Two pairs of parallel, opposite sides
3. Two pairs of congruent (equal), opposite angles
4. Two pairs of equal and parallel opposite sides

You can use proof theorems about a plane, closed quadrilateral to discover if it is a parallelogram:

1. If the quadrilateral has bisecting diagonals, it is a parallelogram
2. If the quadrilateral has two pairs of opposite, congruent sides, it is a parallelogram
3. If the quadrilateral has consecutive supplementary angles, it is a parallelogram
4. If the quadrilateral has one set of opposite parallel, congruent sides, it is a parallelogram

Lesson Summary

You have learned that a parallelogram is a closed, plane figure with four sides. It is a quadrilateral with two pairs of parallel, congruent sides. Its four interior angles add to $360°$ and any two adjacent angles are supplementary, meaning they add to $180°$. Opposite (non-adjacent) angles are congruent. The two diagonals of a parallelogram bisect each other.

Next Lesson:

How To Find the Area of a Parallelogram