What is a Coordinate Plane? — Definition, Quadrants, & Example
Coordinate plane definition
A coordinate plane is an arrangement of perpendicular, regularly spaced number lines, like a fishing net, laid out on a completely flat surface that extends forever in width and length, with no thickness.
Barcelona, Toronto, and New York are all laid out with streets following a grid plan. They are easier to navigate (either on foot or in a car) than cities with haphazard street plans. A coordinate plane, or Cartesian grid, is a grid plan. Like a fishing net, the grid of a coordinate plane lets a lot of stuff drop through, but it holds anything that falls on the lines themselves. Things like circles, sloping lines, polygons, and, on occasion, a fly.
René Descartes and the fly
The 17th century French mathematician and philosopher René Descartes is said to have invented the coordinate system when, as he lay in bed, he noticed a fly on his bedroom ceiling. He wondered how he could describe its movement, so he used one corner of his bedroom as an origin, or starting point, and imagined perpendicular, regularly spaced number lines forming a grid.
We are fortunate that the bedroom ceiling of Descartes was smooth and flat; it made a plane, or completely flat surface, for the fly to crawl upon and inspire one of the greatest mathematicians to create one of the greatest mathematical tools.
Moving on a coordinate plane
René's mouche domestique, living in a mathematician's house, was clearly mathematically inclined and always walked in straight lines. Being a fly, it also tended to move a bit erratically, taking two steps backward for every one step forward. It had a sense of negative numbers, like this:
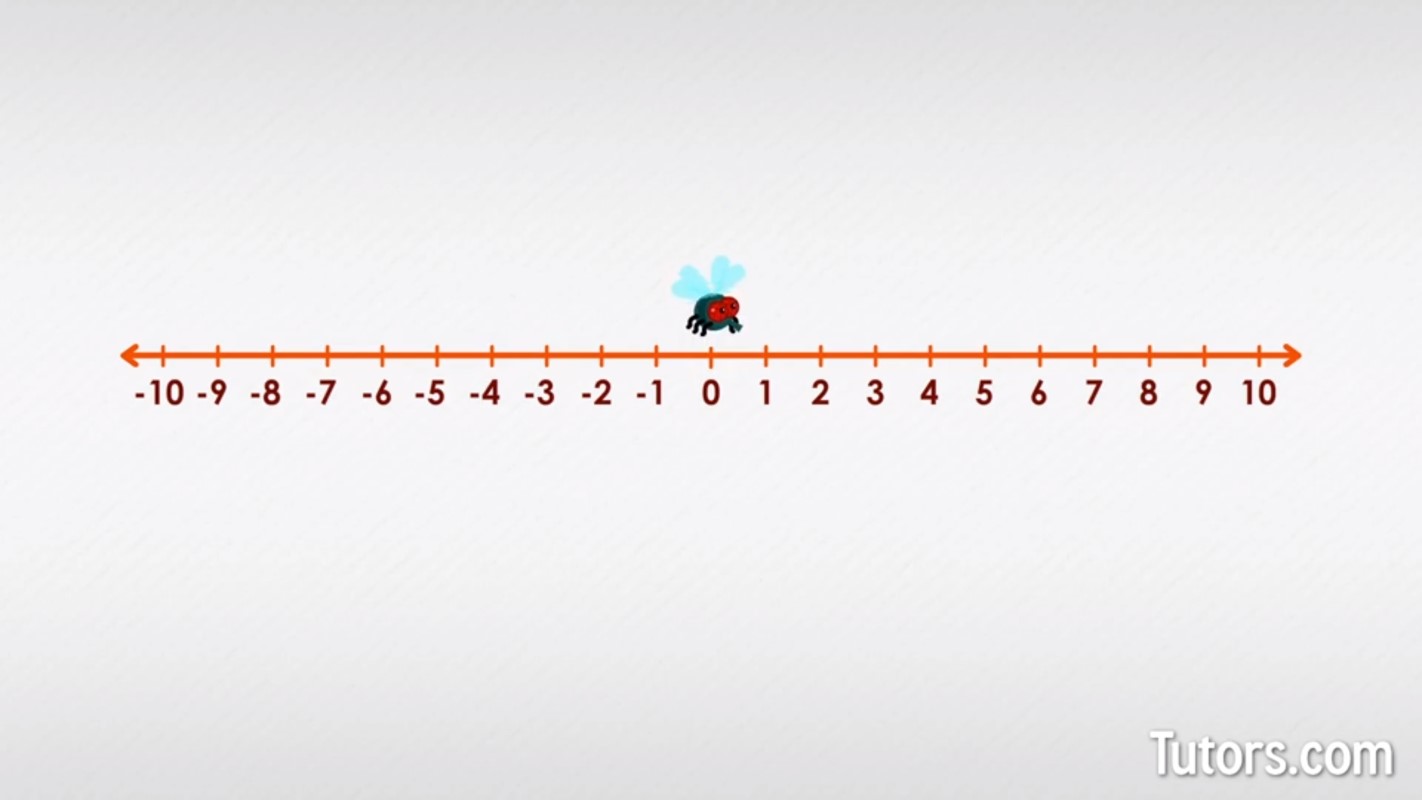
La mouche de René might start out at 0, move to +1, then return to -1. Next la petite mouche starts at -1, advances to 0, and backs up to -2.
But what if the fly turns 90° and heads off in a different direction? We need another number line, perpendicular to our first number line, to chart her motion. We line up the 0 on each number line, and can now measure her movement in two directions.
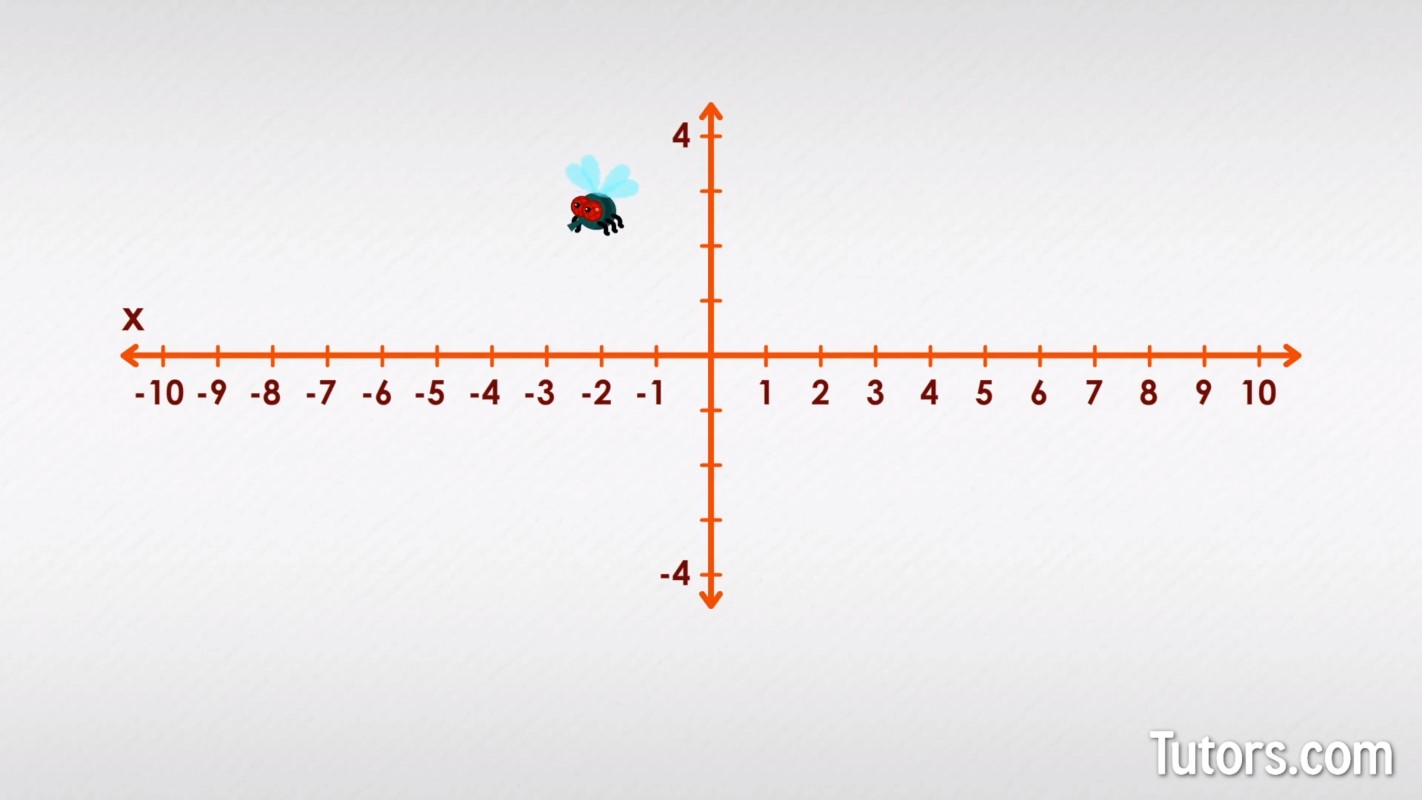
To clearly describe the fly's movement, we need to decide which direction we will mention first, and which we will mention second. Each number line is an axis, with the x-axis going left to right and the y-axis going up to down.
The x-axis value is always given first, followed by the y-axis value. For example, the center of our number lines is (0, 0), and two steps to the left is (-2, 0). Those x and y values form a coordinate pair, which points to a unique position on the coordinate plane.
If we wanted to be imprecise, we could roughly estimate movement with just the two intersecting, perpendicular number lines. Mathematicians are not fond of imprecision, though, so we use multiple number lines in both directions:
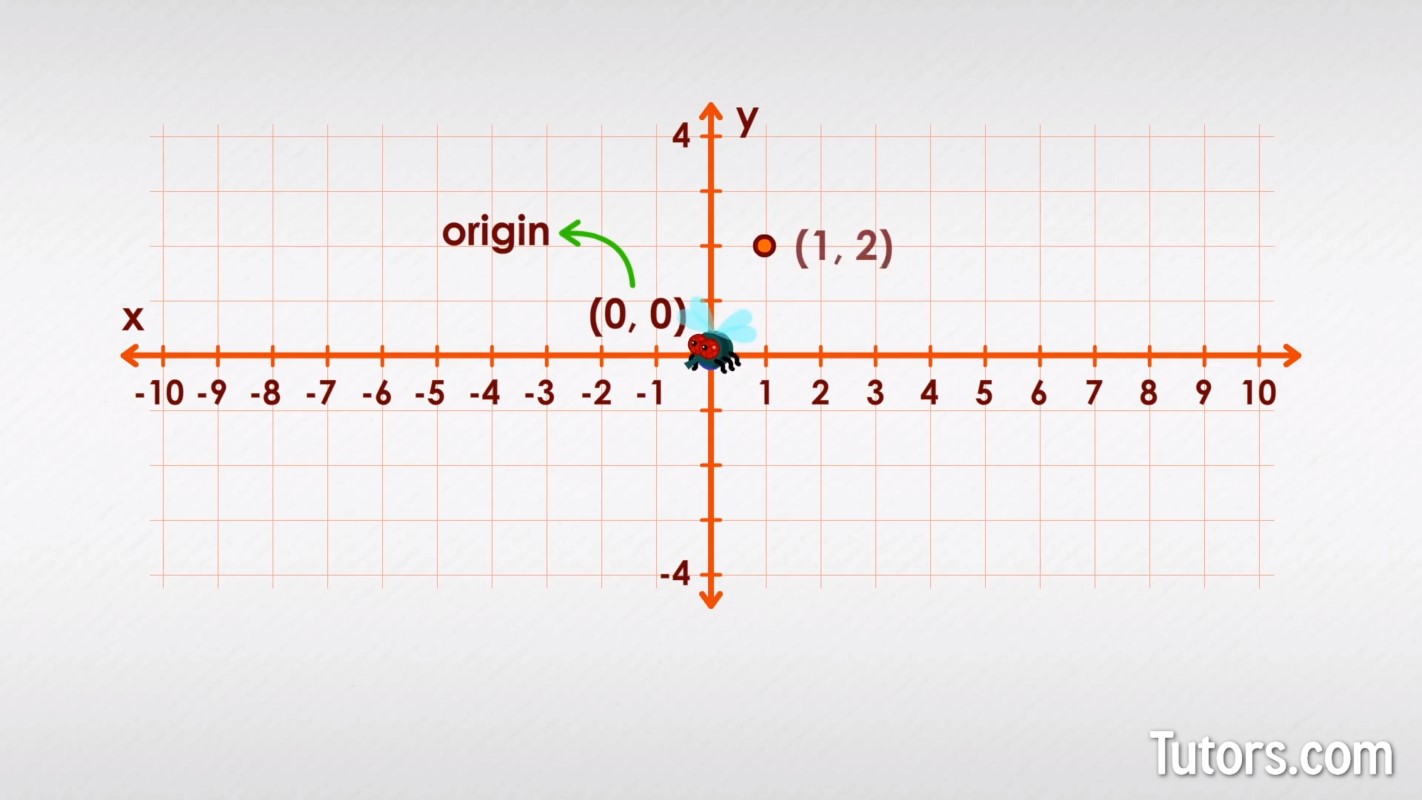
Now we can say the fly, starting at (0, 0), known as the origin, moved to (1, 2). The fly moved one unit to the right, and two units up.
The vocabulary of coordinate planes
To speak accurately about location on coordinate planes, we use specialized vocabulary. We have already seen that the two number lines are called the x-axis (horizontal) and y-axis (vertical). We know that (0,0) is called the origin. Other terms are handy to know, too.
Scale
The number lines can contain numbers of any range. You can have two coordinate grids side by side, one with an x-axis and y-axis starting from -20 and extending to +20. The other coordinate grid could start at -1,000 and extend to +1,000. The two different ranges are the scales of the grids.
In a single coordinate plane, the x-axis can be one scale (say, -10 to +10) and the y-axis can be a different scale (say, -100 to +100). This allows information to be displayed compactly and graphically that otherwise would need huge grids of mostly wasted space.
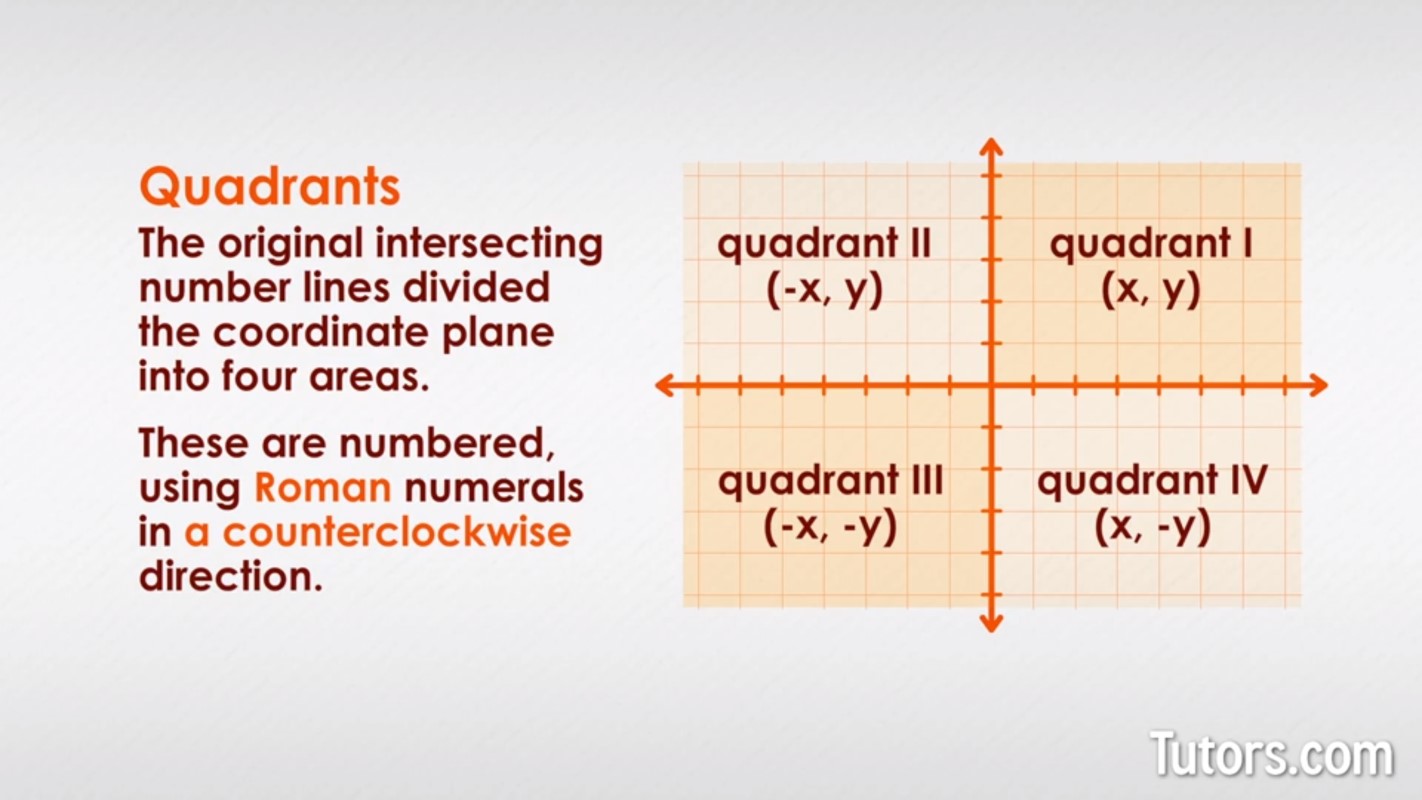
Quadrants
The original intersecting number lines divided the coordinate plane into four areas, called quadrants. These are numbered, by tradition, using Roman numerals in a counterclockwise direction starting with the top, right quadrant, called Quadrant I. This is the quadrant with only positive values for both the x-axis and y-axis. Quadrant II, to its left, has negative x values and positive y values.
Quadrant III has both negative x and y values, while Quadrant IV has negative y values and positive x values.
Nothing prevents a line or flat shape from starting in one quadrant and continuing into another. A circle, for example, could have a center at, say, (1, 3) and a radius of 10 units, allowing it to sweep through all four quadrants.
Intercept
When a line crosses either the x-axis or y-axis, the point is called either the x-intercept or y-intercept. An intercept always happens when the value of the crossed axis is 0:
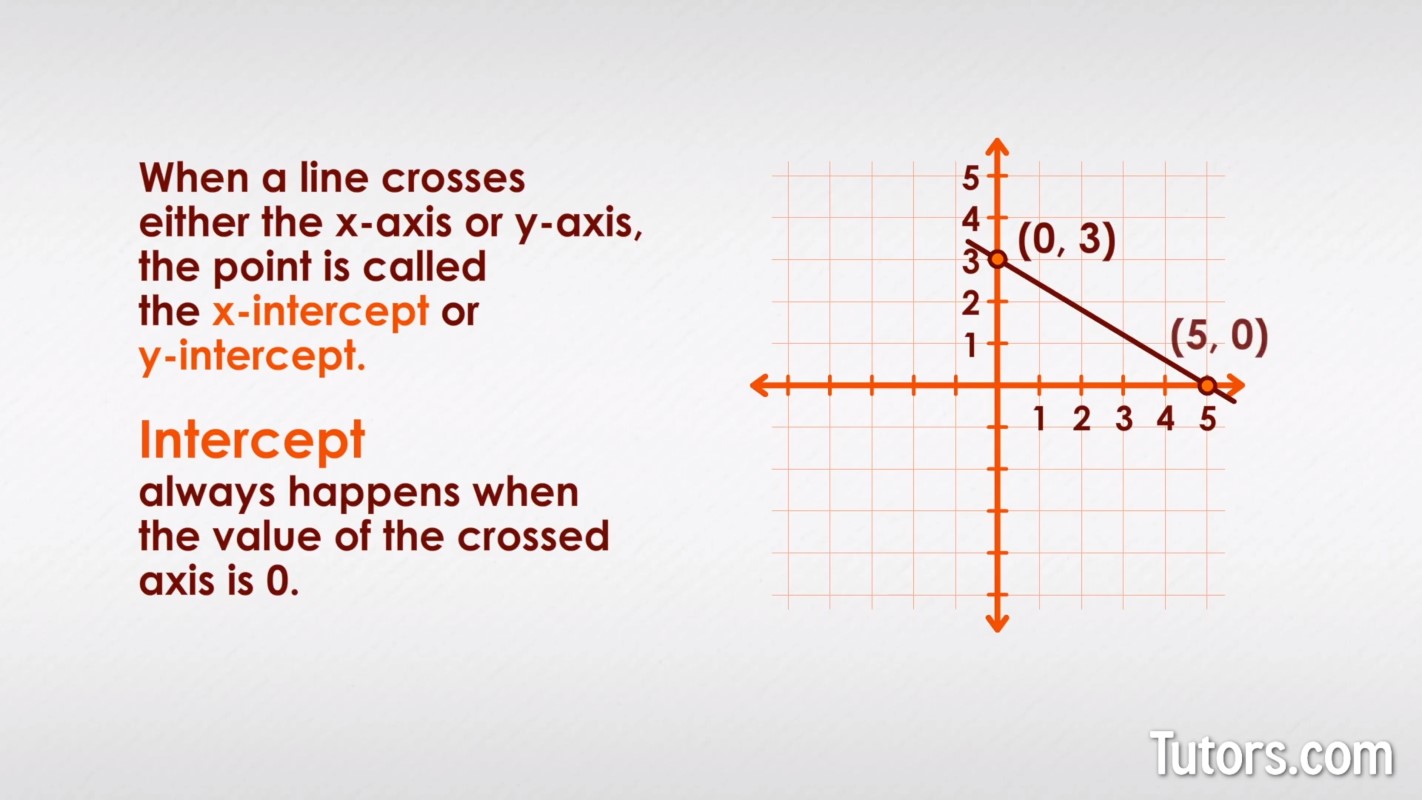
Here the line intercepts the y-axis at 3, along the x-axis value of 0, and intercepts the x-axis at 5, along the y-axis value of 0.
Lesson summary
Now that you have studied the lesson, you are able to identify and define a coordinate plane, relate number lines to a coordinate plane, and name and define terms used in coordinate planes, including axis, coordinate pair, origin, scale, quadrant, and intercept.