Skew Lines
Skew Lines in Geometry (Definition, Examples, & Video)
Unlike so many shapes in geometry, skew lines live in our world. They are part of the geometry of three dimensions, just as you and all your friends are three-dimensional beings. Skew lines can only exist in three dimensions; they cannot be part of the two-dimensional world of polygons and circles.
What are skew lines?
Skew lines are lines that are in different planes, they are never parallel, and they never intersect. On the other hand, parallel lines are lines that are in the same plane and never intersect.
In other words, Parallel lines must exist in two dimensions; they are parallel within the same plane. Skew lines cannot exist in two dimensions and are always in different, non-intersecting planes.

Suppose you wanted to build a big wooden box to hold line segments. You would find the longest line segment and make the box slightly bigger than that, right? What if, though, you wanted to hold rays, or lines?
No box exists that could hold either, because rays continue in one direction forever, and lines continue in two directions forever.
Skew lines are what you would have if you tried to store lines in a big box. Like a bunch of infinite, double-ended arrows, they would not cooperate.
Skew lines have several identifying properties that make the big wooden box impractical:
They continue in two directions forever
They are in different planes
They are never parallel
They never intersect
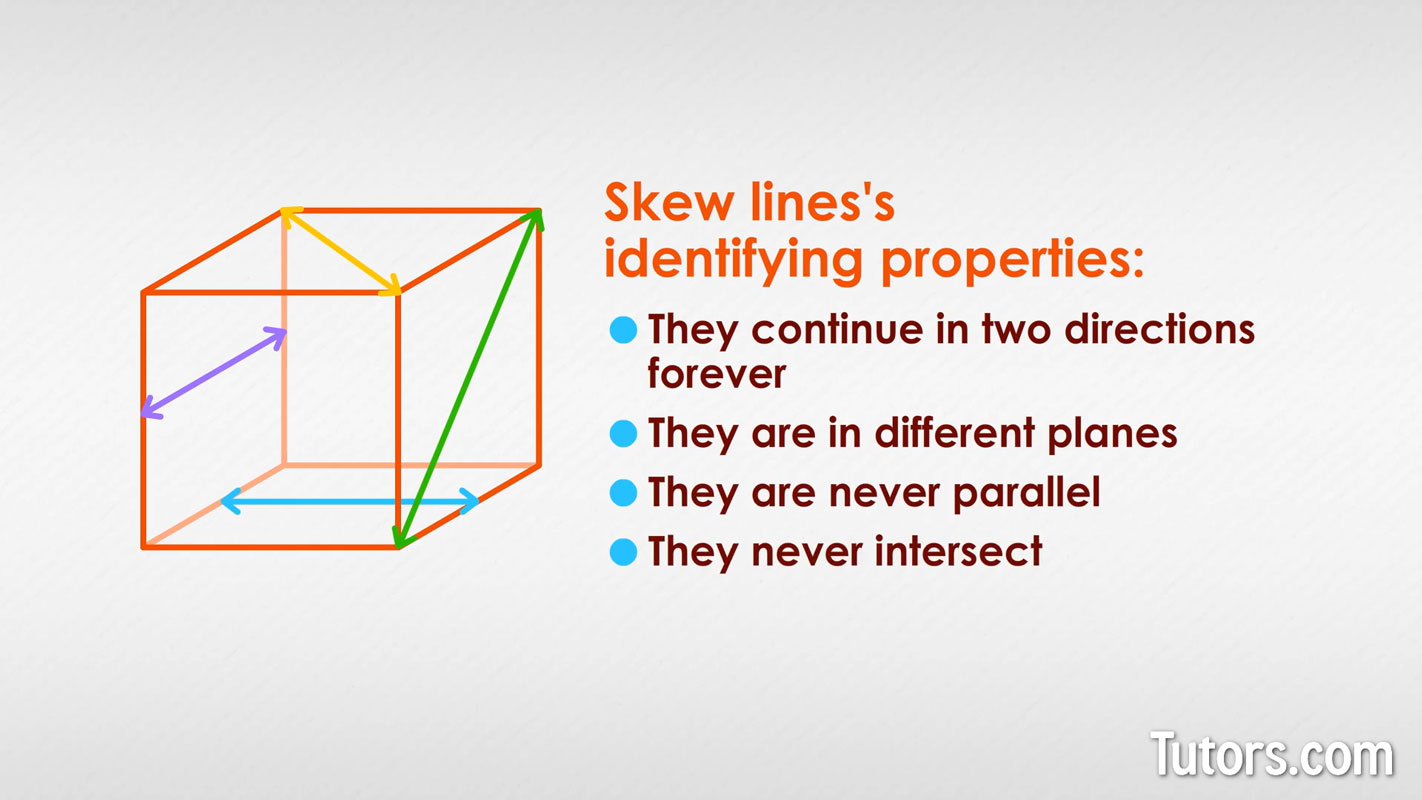
Skew lines examples
Please step into our imaginary geometry elevator. An elevator is a rectangular prism (six faces, eight vertices, 12 edges, and so on).
The inside walls are all dry-erase boards (how thoughtful!). You happen to have a dry erase marker and a straightedge in your hands (of course you do!), so you draw a line on the side wall of the elevator, stretching from the top of the elevator car to the floor, complete with arrowheads.
That looks nice, so you draw another line on the opposite, side wall, going from the car's front to back.
No worries, it is not graffiti; it's dry erase! Notice the two lines are in two separate planes, separated by all the space you are occupying. More, one line is going up and down, while the other is going front to back.
Those are skew lines. They are not parallel, and they will never intersect (they are in two different planes).
Inside the elevator, you realize you are looking at 12 edges (where planes intersect):
Four ceiling edges
Four wall edges
Four floor edges
Select any edge. Then select another edge that is:
Not parallel to your first edge and
Does not share either plane that created the first edge
Do those two things, and you have found skew lines! The top, horizontal line of the elevator, for example, is skew to either rear, vertical line. Those lines will never intersect, and they are not parallel.
Diagonals
Since skew lines must exist in three-dimensional space, you can include diagonals in your search for skew lines. A line cutting diagonally from one corner of the elevator's ceiling to another corner of the same ceiling is skew to the four edges of the floor.
Get more dramatic: a line from a top corner of the elevator to an opposite, bottom corner -- slicing right through the center space of the elevator (where you are standing) -- is skew to the two vertical wall corners untouched by the line.
Testing skew lines
Lines, line segments and rays can all be skew. You can perform a quick check of suspected skew lines just with your straightedge. Align it on one line and physically move it to the other line. If you have to twist, turn, rotate or otherwise change the orientation of your straightedge to align with the second line, then the two lines are skew.
Another way to test it is to think of hanging wet bed linens from one line to the other. If you can imagine hanging a bed sheet between the two lines so the bed sheet hangs completely flat (like a plane), the two lines are not skew. If the bed sheet has to twist, the two lines are skew.
Lesson summary
Now that you have completed this lesson, you are able to recognize and identify skew lines, define skew lines, compare and contrast skew lines with parallel lines in two dimensions, and test for skew lines.