How To Find the Area of a Rhombus

Table of Contents

1. What is a Rhombus?
2. Area of a Rhombus Formula
3. How to Find the Area of a Rhombus
• Formula Using the Altitude and Side
• Formula Using the Side and Angle
• Formula Using the Diagonals

What is a Rhombus?

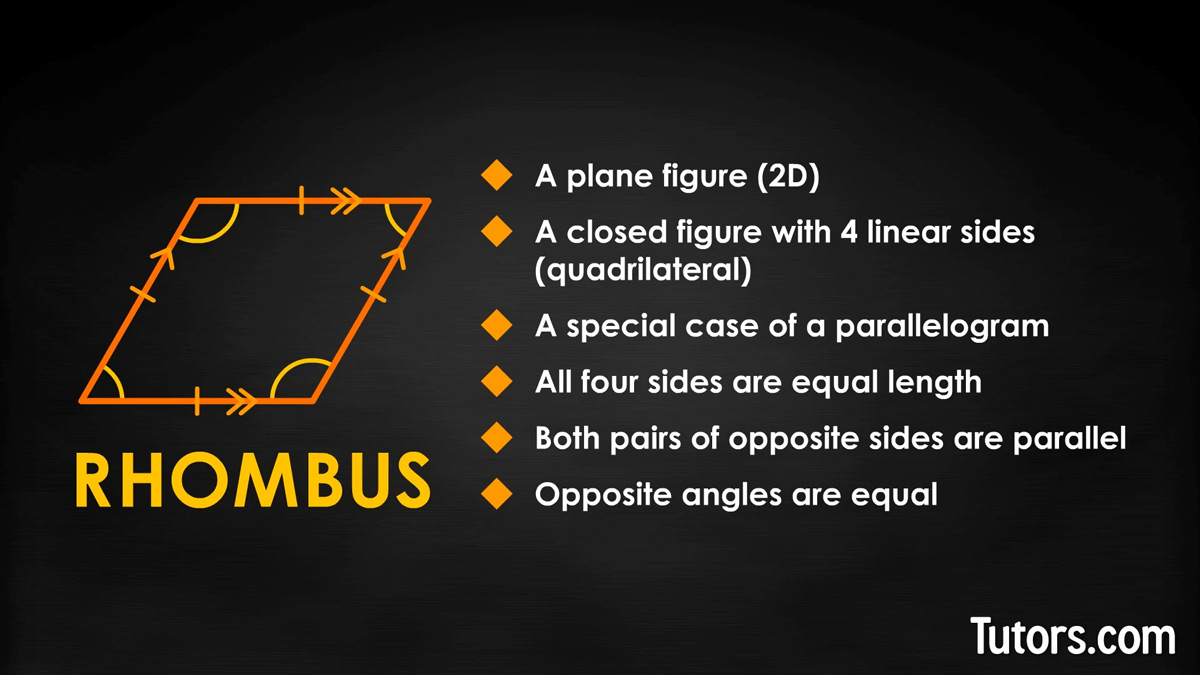
A rhombus is a plane figure, so it is two-dimensional. It is a closed figure with straight (linear) sides, one of the many quadrilaterals (four-sided shapes). It is a special case of a parallelogram. All four sides are of equal length, and both pairs of opposite sides are parallel. Opposite angles are equal, too. That's it!

A rhombus can also be called a rhomb, lozenge, or diamond. A square is a rhombus with four equal (right) angles.

Sometimes you see a rhombus with two sides horizontal, as if a square has been run into by a bus and tilted over (that is a handy mnemonic to remember its name: run, bus; rhombus). In this presentation, the altitude (height) of the rhombus can be very easy to see.

Sometimes the rhombus is drawn so one of its two diagonals (lines connecting opposite vertices) is horizontal, making the diamond shape more obvious.

These diagonals also bisect each other, which means they divide the rhombus up into four right-angle triangles. The squares of the lengths of the two diagonals are always four times the square of a side.

For such a simple shape, a rhombus has many parts and measurements. Knowing how to use these measurements can help you find area, perimeter and other facts about the rhombus.

Area of a Rhombus Formula

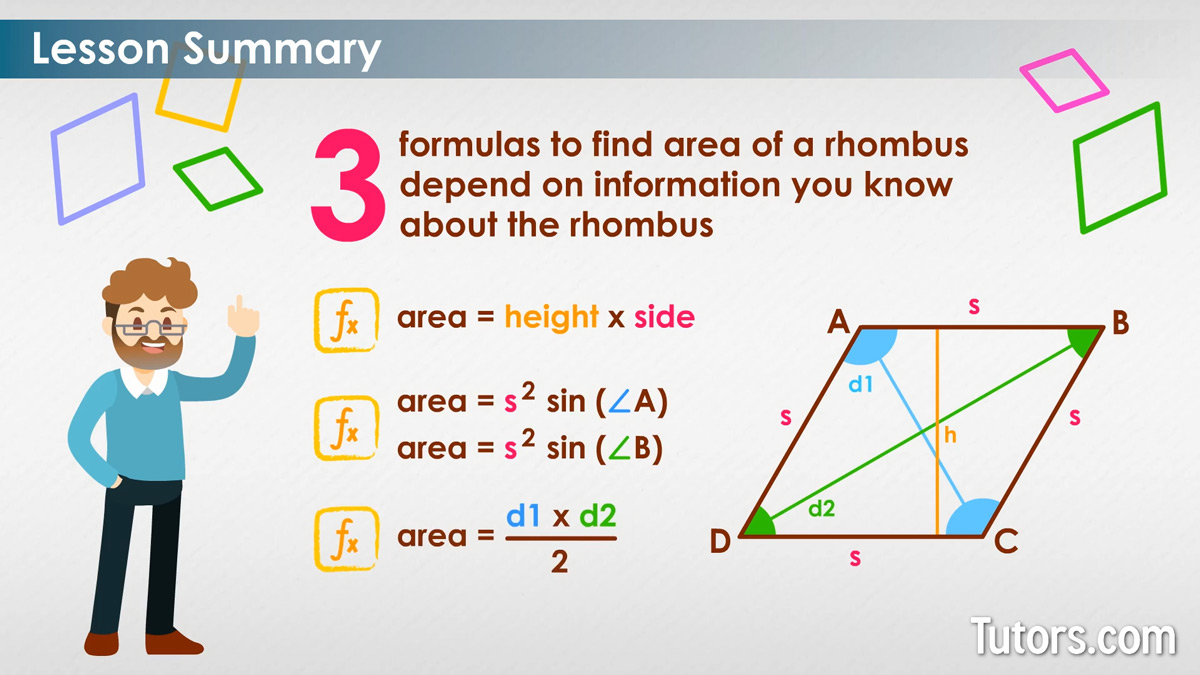
There are three different formulas for finding the area of a rhombus. There is one using the altitude and side, another using the side and angle, and one for the diagonals. The three formulas to find area depend on information you know about the rhombus.

1. If you know Altitude (height) and side s the formula is:
   $area = height \times s$
2. If you know the length of one side s and the measure of one angle the formula is:
   $area = s^{2 }\sin \left(\angle A\right) = s^{2 }\sin \left(\angle B\right)$
3. If you know the lengths of the diagonals the formula is:
   $area = \frac{(d_{1 }\times d_2)}{2}$

How to Find the Area of a Rhombus

Let's construct a rhombus with sides $s$ and four vertices with interior angles $A$, $B$, $C$ and $D$. We can connect opposite angles with diagonals $d_1$ and $d_2$. Connecting one side to the other with a perpendicular line gives the altitude or height. Our rhombus has:

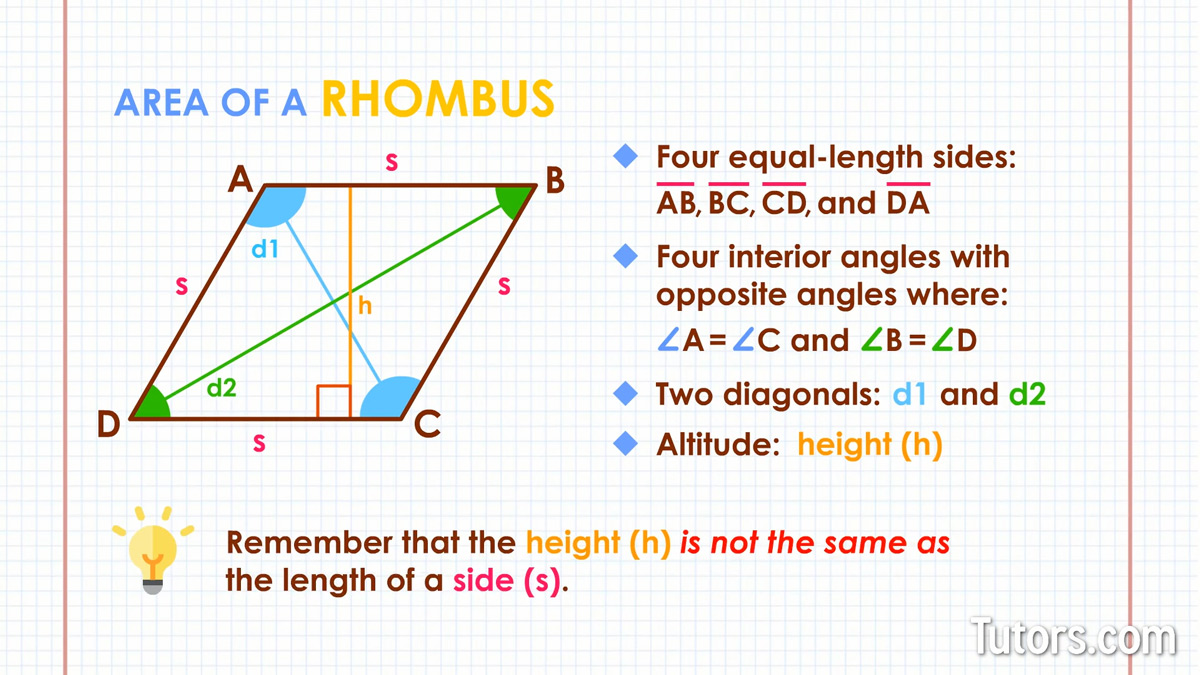
• Four equal-length sides: $AB$, $BC$, $CD$ and $DA$
• Four interior angles with opposite angles equal: $\mathrm{\angle }a=\mathrm{\angle }c$ and $\mathrm{\angle }b=\mathrm{\angle }d$
• Two diagonals: $d_1$ and $d_2$; only in a square will these be equal-length diagonals
• Altitude, or height -- When the rhombus sits with two sides horizontal (flat), the height $h$ is the distance from one side to the opposite side; the line segment perpendicular to one side, connecting to the opposite side

Since the four sides are equal, if you know the length of any side $s$, you know the length of all four sides.

Since opposite angles are equal, and the four angles add to $360°$, if you know one angle, you can find all angles. Since opposite sides are parallel, adjacent angles in a rhombus add to $180°$.

For finding area, you need to know the height, or altitude, $h$, of the rhombus.

Formula Using the Altitude and Side

If you have a mental picture of a rhombus being a tilted square, this first method will make a lot of sense.

If the rhombus were a square, its area in square units would be side x side, right? Well, when the rhombus is tilted, you could imagine cutting off the triangular part on one side of the rhombus and sliding it over to the matching other side, restoring the shape to its square-ness.

You cannot actually cut up every rhombus you meet, though, so consider what that one constructed, perpendicular side really is: the height, or altitude, of the rhombus.

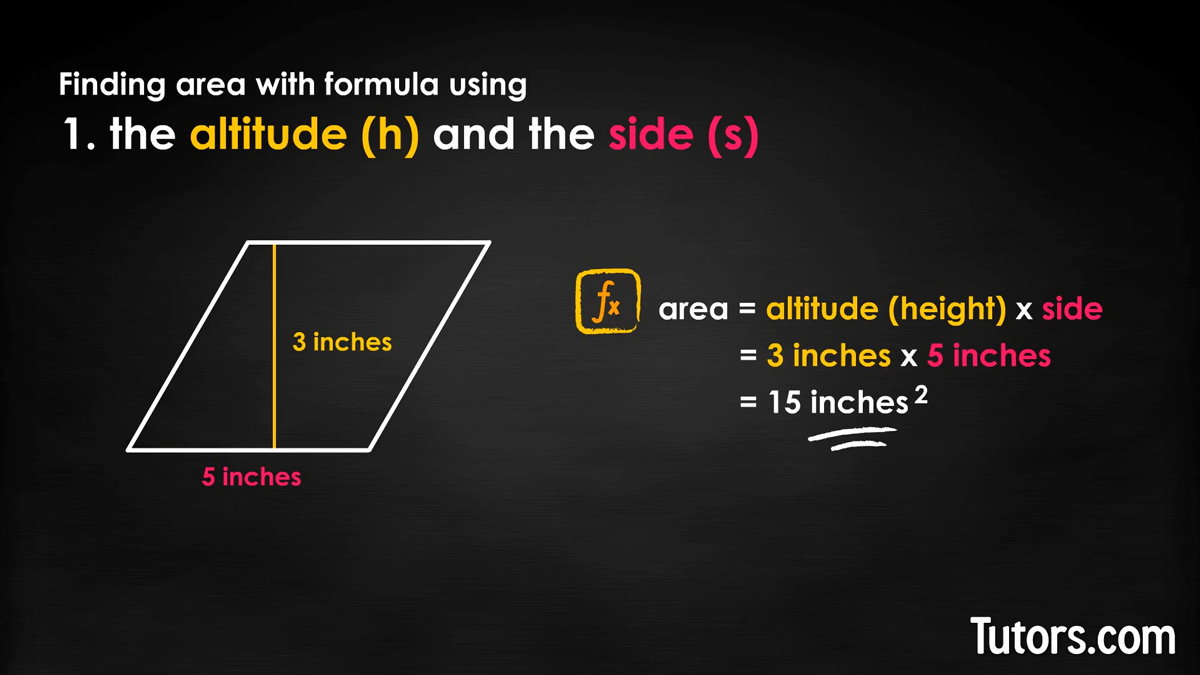
So, the first and perhaps easiest way to find area of a rhombus is to find the length of one side and the rhombus's height. Multiply these and you have the area, in square units:

Example:

So, if you had a rhombus whose altitude is 3 inches with sides that are 5 inches, then the area of this rhombus is:

$3 inches \times 5 inches = 15 inche{s}^2$

Another example is where side s is 15 feet and the height of 11 feet. This area of this rhombus is:

$15 \times 11=165 square feet$

Formula Using the Side and Angle

The second way to find the area of a rhombus is by knowing the length of a side s and the measure of one angle $(\angle A or \angle B)$. Here you need to find the sine of the angle, but the formula is still straightforward:

You can see that these two formulas give the same result, so

$area = s^{2 }\sin \left(\angle A\right) = s^{2 }\sin \left(\angle B\right)$

Example:

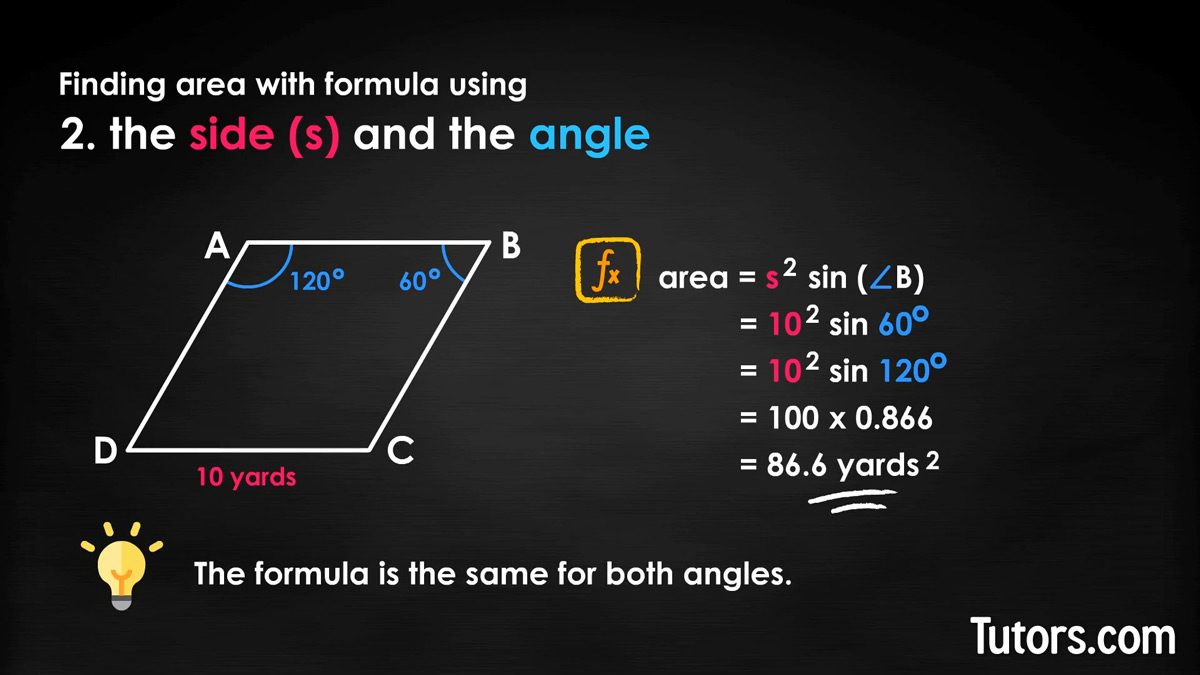
In a rhombus with sides of 10 yards and interior adjacent angles of $60°$ and $120°$ then to find the area of this rhombus, we would plug this into our formula for area using the side and an angle.

$area = {10}^2 \sin \left(60°\right)$

which is also the same as

$area = {10}^2 \sin \left(120°\right)$

Then, we multiply these two numbers together:

$area = 100 \times 0.866$

Then, we get our answer:

$area = 86.6 square yards$

The sine of $60°$ and $120°$ is the same, $0.866$

Formula Using the Diagonals

Remember that the diagonals of a rhombus always intersect each other at right angles, and bisect each other. That means the two diagonals form two sides of a square that is twice the size of the rhombus.

You can find the area in square units of the rhombus by multiplying the lengths of the two diagonals ($d_1$ and $d_2$) and dividing by two.

If our rhombus only has the measurements for the diagonals, this is the formula we would use.

Example:

If our rhombus had diagonals measuring 24 and 18 meters in length, then to find the area of this rhombus, we would plug the numbers into our formula.

$area = \frac{(24 \times 18)}{2}$

We multiply the two diagonals:

$area = \frac{\left(432\right)}{2}$

Then we get our answer:

$area = 216 square meters$

Lesson Summary

You have reviewed what a rhombus is, how it fits into the family of quadrilaterals, what its various parts are, and how to find its area.

Next Lesson:

Kites in Geometry