How To Find the Area of a Parallelogram
What is a parallelogram?
Any shape with the word "parallel" in it gives away an important insight: the four-sided shape will have two pairs of opposite, parallel sides.
As a quick refresher, a parallelogram is a plane figure, so it is two-dimensional. It is a closed figure with straight sides, a type of quadrilateral (four-sided shape). Because opposite sides are parallel, opposite angles and sides are congruent (the same).

Suppose you built a crate to hold, say, oranges, but you forget to put a bottom on it. Two of the crate's sides are 12 inches and the other two are 18 inches.
If you turn the crate so one of its 18-inch sides is flat on a table, the crate naturally leans (because it had no bottom to hold the four sides rigid).
The leaning crate forms a parallelogram. If you push or pull the crate so it leans more or less, every shape it takes is a parallelogram. Its sides never change their length, but the crate's height (or width) changes.
Area of a parallelogram
If you noticed the three special parallelograms in the list above, you already have a sense of how to find area. Finding the area of a rectangle, for example, is easy: length x width, or base x height.
The length of any linear geometric shape is the longer of its two measurements; the longer side is its base.
For any parallelogram, we need to know the length of a longer side (base), and its width. This is where things get tricky, because the distance along either short side is not necessarily its width.
Think of our wobbly orange crate; we could nearly collapse it flat, but its two short sides would always be 12 inches.
How to find the area of a parallelogram
We can name the various parts of our orange-crate parallelogram. The four vertices (corners) are A, B, C and D. The two long sides, at 18 inches, are AB and CD. Side CD forms the base (b) of our parallelogram.
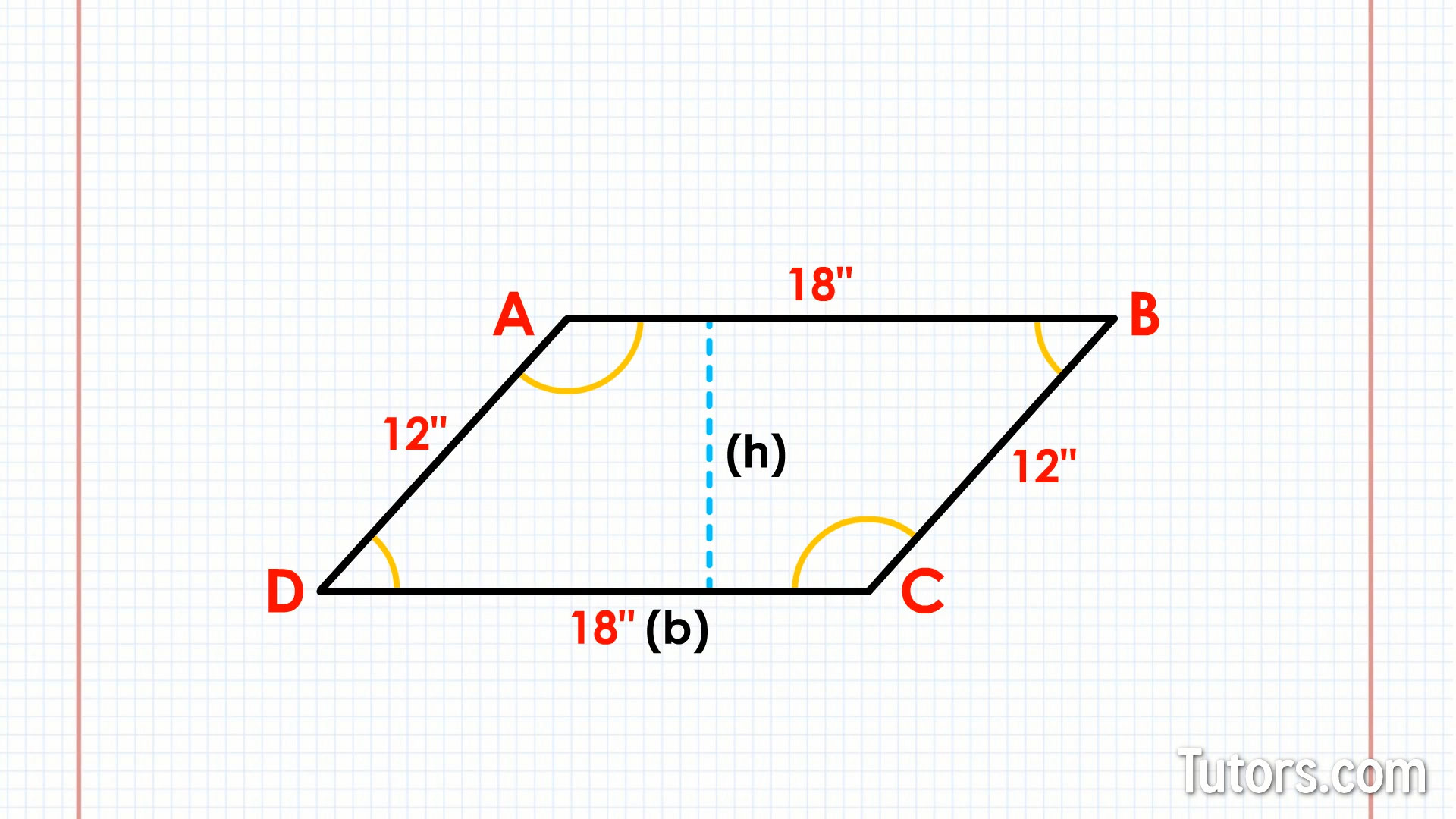
The two short sides, at 12 inches, are BC and DA. The width (or height) of the crate – the distance straight across from the base to the other side – could vary depending on the inside angles of vertices A, B, C and D.
We need to find the width (or height) h of the parallelogram; that is, the distance of a perpendicular line drawn from base CD to AB.
Area of a parallelogram formula
If you know the length of base b, and you know the height or width h, you can now multiply those two numbers to get area using this formula:
Then, we get our answer:
How to calculate the area of a parallelogram
That calculation seems too simple and does not seem to take into account the angled sides, does it?
But consider, we can move the parallelogram and change its angles. At some point, we can make every interior angle a right angle and get a rectangle. That means, no matter the angles we push and pull the parallelogram into, the four sides enclose the same area.
Another way to think of it is to consider cutting off a triangle from, say, the left side of the parallelogram to leave a nice, perpendicular corner. Move that cut off triangle over to the right side and the parallelogram is suddenly a rectangle.
The area of a rectangle is easy, remember? Length x width in square units, which is the same as base x height (b x h) in square units.
Area of a parallelogram example
A parallelogram has sides 35 cm and 17 cm, with a height of 11 cm. What is its area?
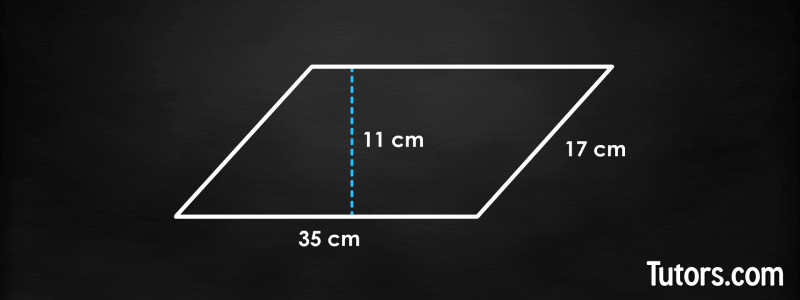
Start by plugging the base and height into our formula:
Then, we multiply these two numbers together and get our answer:
Lesson summary
We have reviewed what a parallelogram is, what its parts are, and how to find its area, which is always expressed (written) in square units. The parallelogram is a quadrilateral with opposite sides parallel; it always has four sides, and one longer side will always be its base.