How To Construct 30°, 60°, 90° and 120° Degree Angles

Table Of Contents

1. Construction of Angles
2. How To Construct A 90 Degree Angle
3. How To Construct A 60 Degree Angle
4. Steps Of Construction Of A 60 Degree Angle Using a Compass
5. How To Construct A 30 Degree Angle
6. How To Construct A 120 Degree Angle Using A Compass

Construction of Angles

One of the most beautiful aspects of geometry is how neatly everything fits together. Knowing how to bisect a line segment means we know how to make a $90°$ angle. Knowing an equilateral triangle has three $60°$ angles makes an easy job of constructing a $60°$ angle with only a compass, a pencil, and a straightedge. Everything fits together. You need nearly the same tools Euclid used, thousands of years ago:

• A drawing compass
• A straightedge
• A pencil
• Some paper

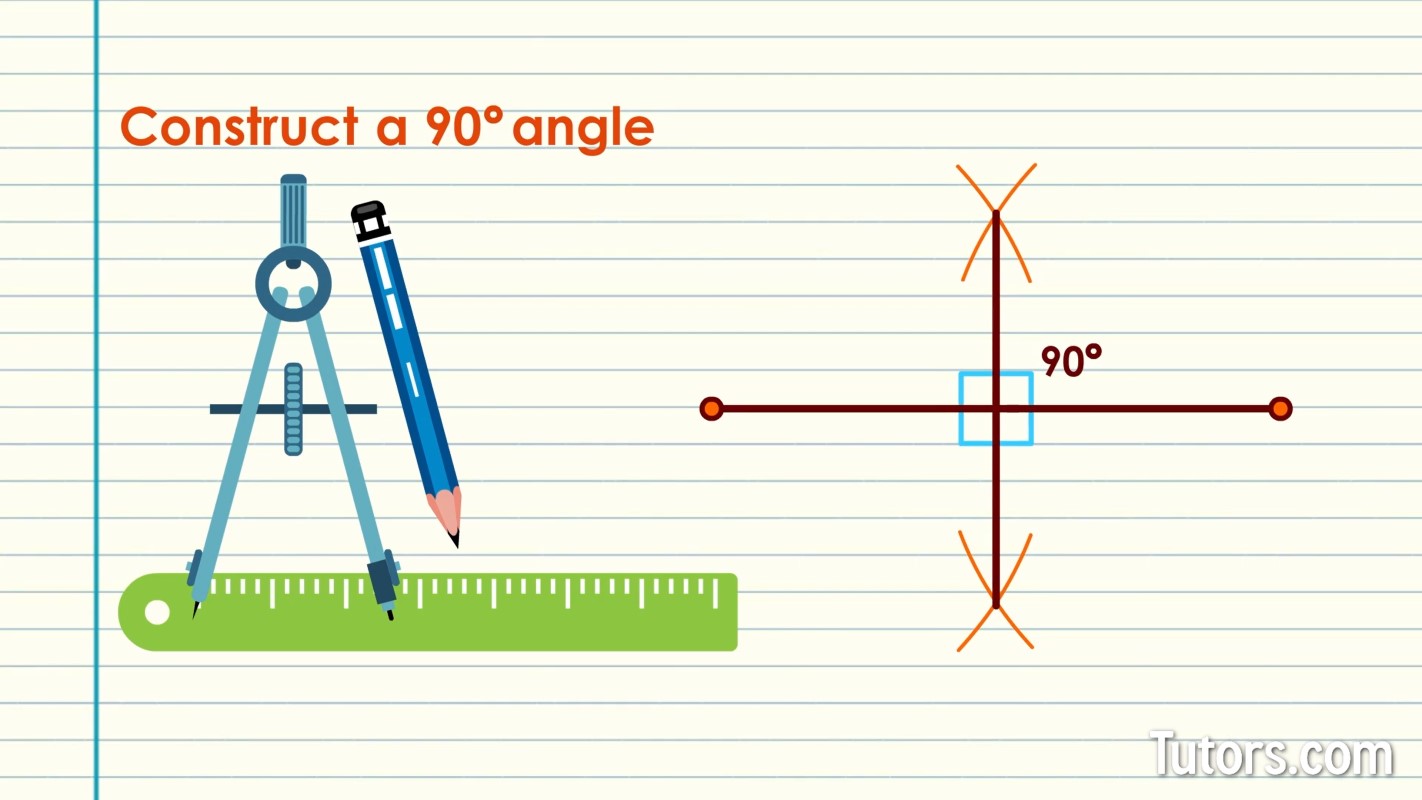
How To Construct A 90 Degree Angle

1. On the paper, draw a line segment longer than the ray of a the $90°$ angle you need.
2. Locate two points on the line segment at either end.
3. Open the drawing compass to extend a bit beyond half the distance of the line segment (do this visually; no need for numbers).
4. Swing an arc above and below the line segment.
5. Without changing the compass, relocate it to the other endpoint.
6. Swing another arc above and below the line segment. The two arcs should cross above and below the line segment.

Connecting the arc intersection points with the straightedge will produce a neat, sure $90°$ angle, with your transversal and the original line meeting at four right angles!

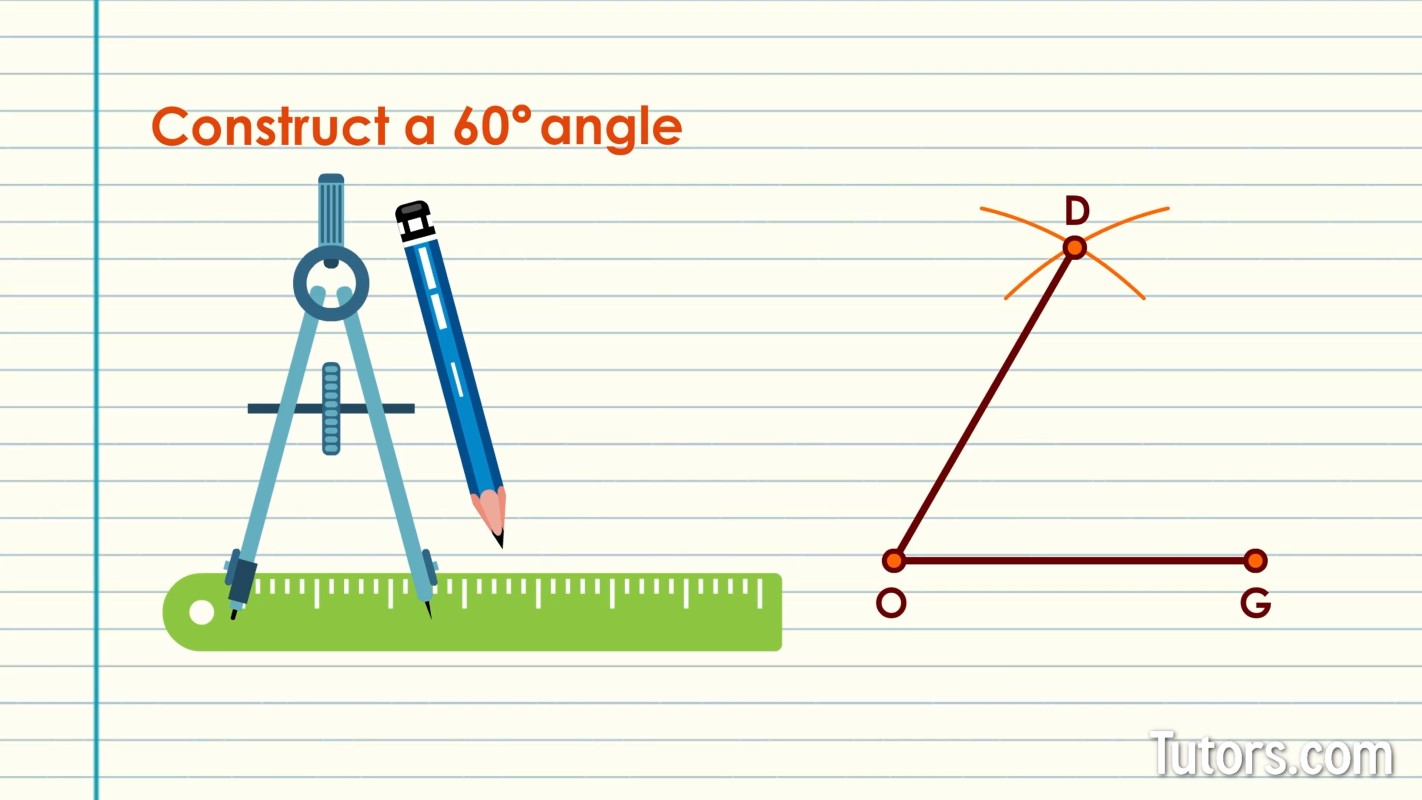
How To Construct A 60 Degree Angle

Something practically mystical surrounds $60°$. It forms interior angles of equilateral triangles. It is exactly 1/6th of a circle. Half of it plus itself forms a right angle. You could go on and on.

Steps Of Construction Of A 60 Degree Angle Using a Compass

Making a $60°$ angle begins by remembering that equilateral triangle.

1. Construct a line segment with a straightedge. Label its endpoints. In our drawing, we will call them $Points O$ and $G$.[insert drawing of left-to-right line segment OG]
2. Place the drawing compass needle on $Point O$ and adjust it to meet $Point G$.
3. Swing an arc upward from $Point G$ high above the line segment.
4. Without adjusting the compass, relocate the needle to $Point G$.
5. Swing an arc upwards, so it crosses the first arc.
6. Use the straightedge to construct a line segment from $Point O$ up to the point of intersection of the two arcs.
7. Label that line segment's new endpoint $Point D$.

The angle created from $Points D$ to $O$ to $G$, by striking three congruent lengths, is $60°$. If you wanted, you could connect $Points D$ and $G$ and form the equilateral triangle. Hey, $DOG$, you did it!

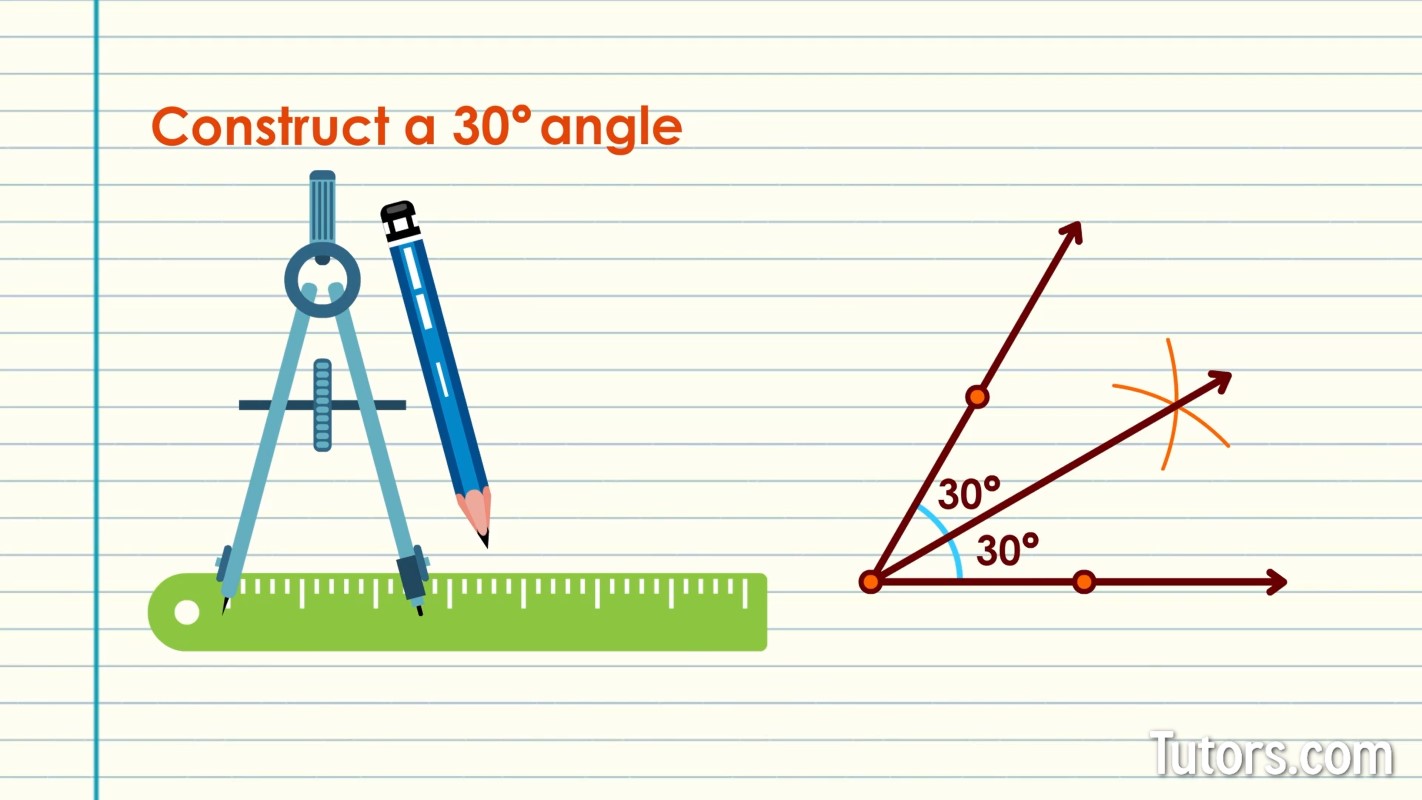
How To Construct A 30 Degree Angle

A $30°$ angle is half of a $60°$ angle. So, to draw a $30°$, construct a $60°$ angle and then bisect it.

First, follow the steps above to construct your $60°$ angle.

Bisect the $60°$ angle with your drawing compass, like this:

1. Without changing the compass, relocate the needle arm to one of the points on the rays. Swing an arc on the inside of the angle.
2. Without changing the compass, relocate the needle arm to the other ray's point. Swing an arc on the inside of the angle.
3. Use the straightedge to connect the intersection of the two arcs with the vertex of the $60°$ angle. That line segment is an angle bisector, yielding two $30°$ angles.

How To Construct A 120 Degree Angle Using A Compass

Remember how we said everything in geometry fits together? What is the supplementary angle to an angle of $120°$? In other words, what angle must we add to $120°$ to get $180°$?

Did you say $60°$? Sure, a $120°$ angle is the adjacent angle to any of the $60°$ angles you already constructed!

To construct your $120°$ angle, construct a $60°$ angle and then extend one of its sides far past the vertex, like this:

[insert animation of 60° angle constructed, then run out the side and highlight the 120° angle adjoining it]

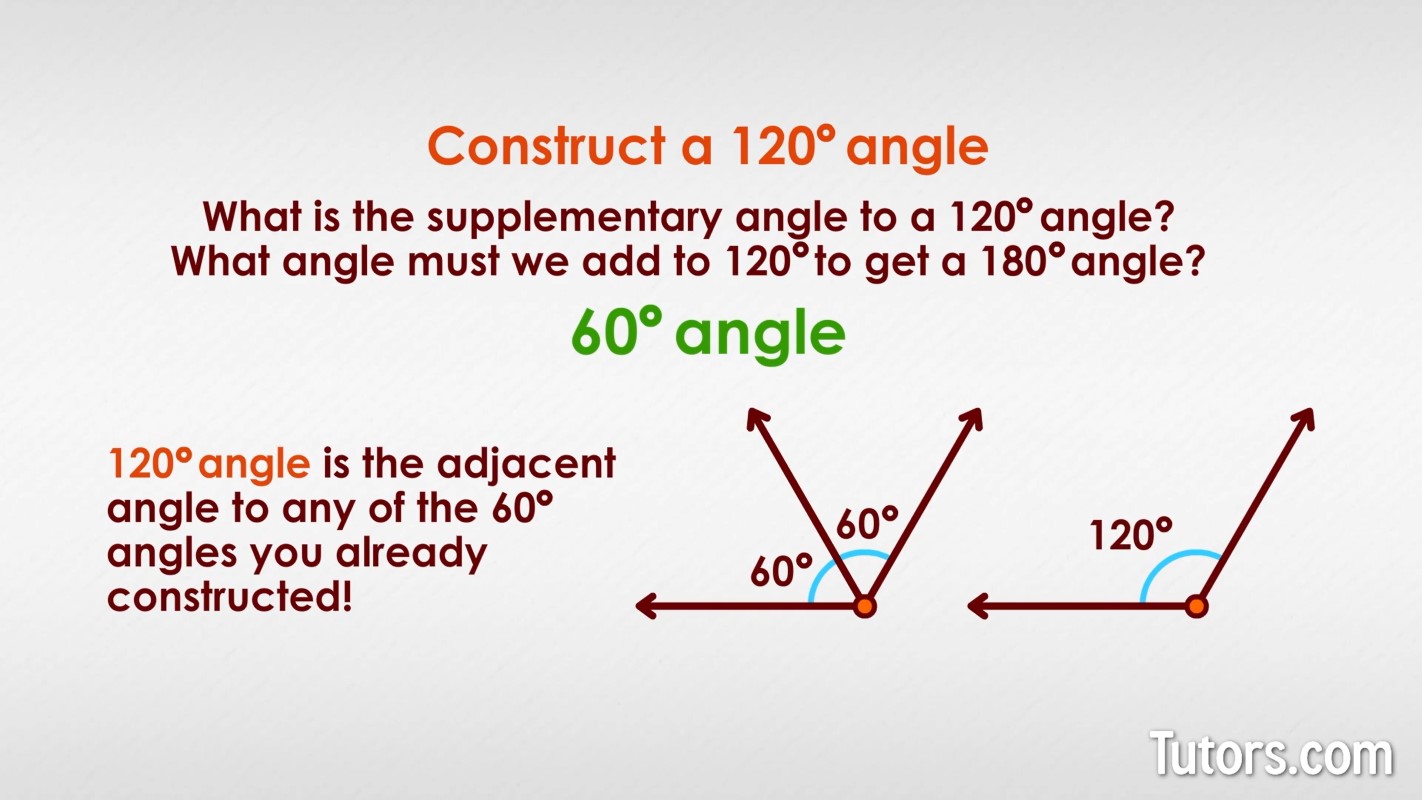
That angle beyond the $60°$ angle is your $120°$ angle.

None of your constructions required numbers or measurement. Euclid would be proud of you!

Next Lesson:

Construct An Equilateral Triangle