Collinear Points in Geometry (Definition & Examples)

Mathematics is a branch of science. Many scientists consider mathematics a pure science, one that is equal parts precision and imagination. Collinear points is a fancy, but a precise, way of describing points in a line.

Table Of Contents

1. Collinear Points Definition
2. Collinear Points in Real Life
3. Collinear Points in Geometry
4. Collinear Points in Geometry
5. Collinear Points Examples

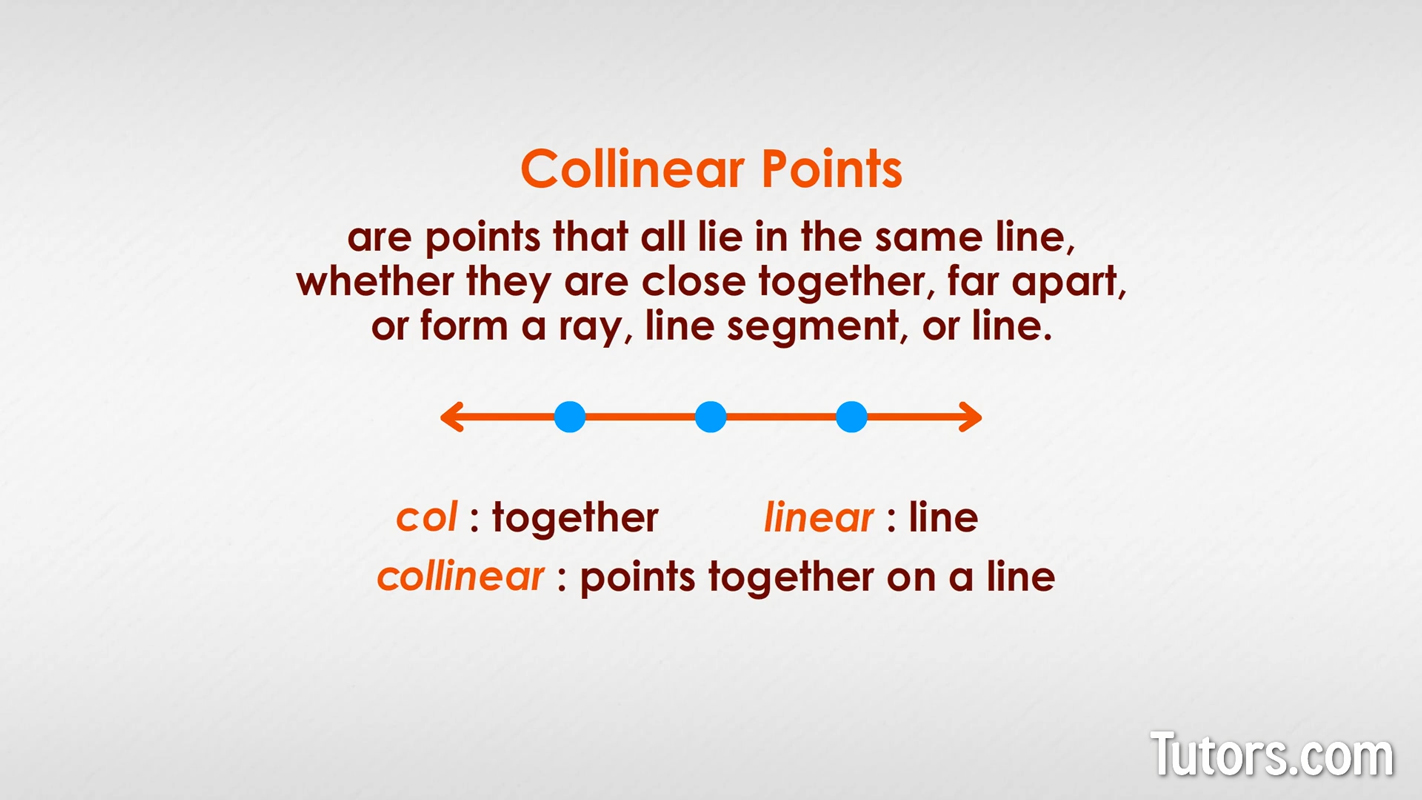
Collinear Points Definition

Mathematicians use words very exactly. In Euclidean geometry, Collinear points are points that all lie in the same line, whether they are close together, far apart, or form a ray, line segment, or line. A little Latin helps: col + linear = collinear.

The combination, collinear, means points together on a single line.

Collinear Points in Real Life

Anytime you have a series of individual items in a single straight line, you have models of collinear points. Suppose you have eggs in a carton; each egg in one row is a collinear point:

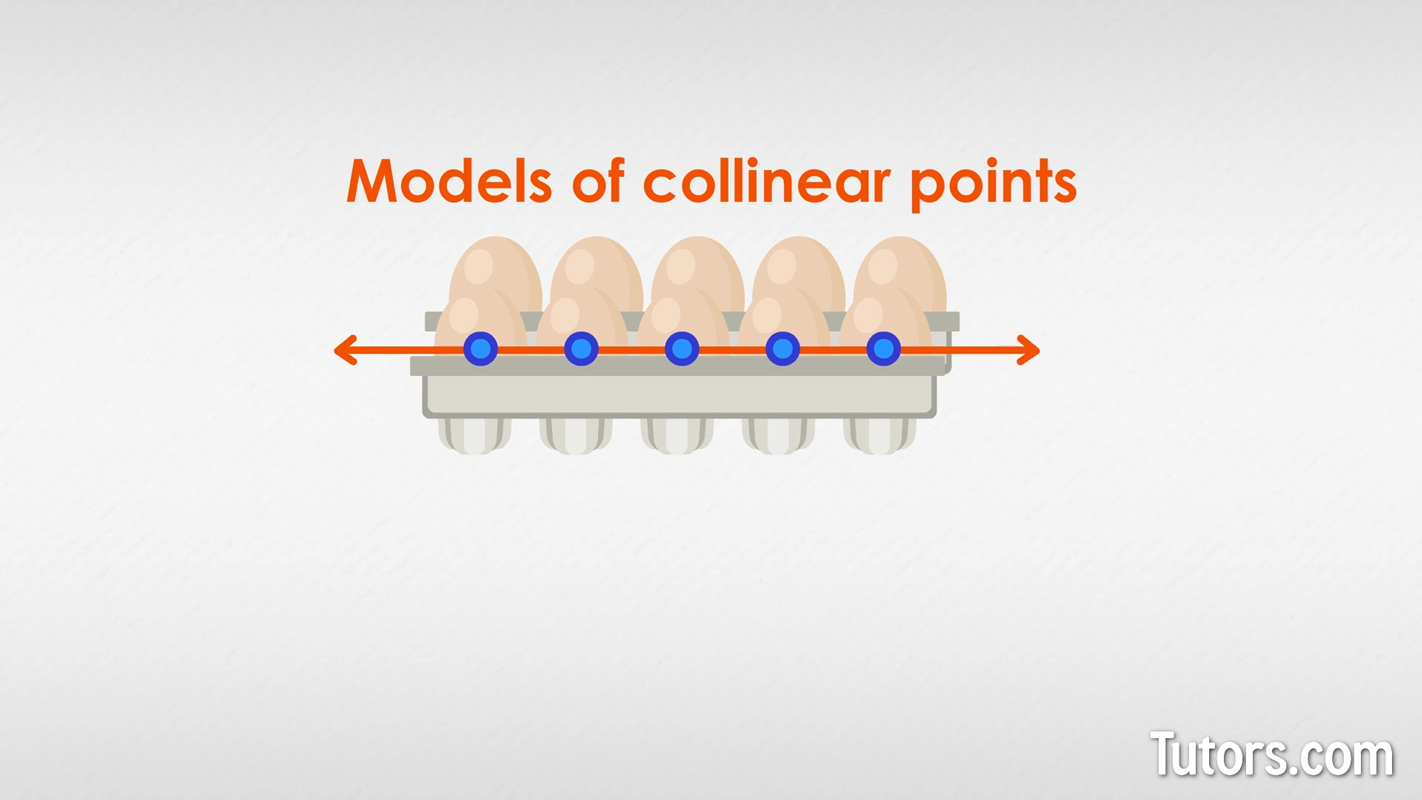
Students seated at a long cafeteria table are collinear. Football players on the line of scrimmage are collinear. Rings on a shower curtain, plants in one row in a garden, numbers on a ruler, moviegoers in a ticket line, and commuters seated on a train are collinear.

For real-life examples to be good models of collinear points, you need to be able to draw a straight line through them. Think of the individual kernels on one row of an ear of corn.

Collinear foods are found all over the globe. In Japan, people enjoy Dango; sweet little dumplings arranged three to five on a skewer.

Sosatie is a South African dish of little cubes of lamb or mutton interspersed with dried apricots, red onions, and mixed peppers, all on skewers.

Frigărui, a Romanian kebab, is cubes of meat with bacon, onions, tomatoes, bell peppers, and mushrooms.

In all cases, the little bits of food are lined up on a bamboo or wood skewer, so they are all points on a single line. They are all collinear.

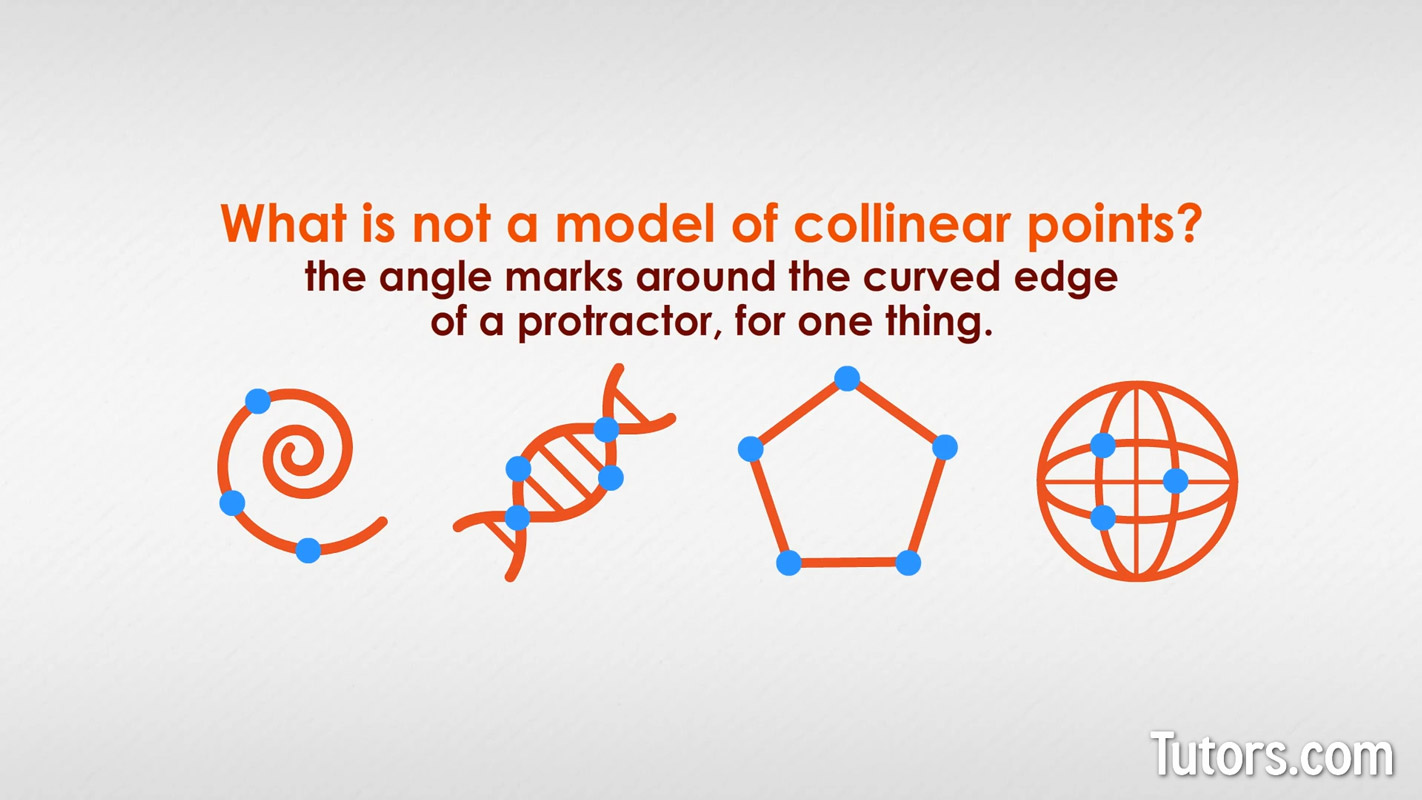
Non-Collinear Points

What is not a model of collinear points? The angle marks around the curved edge of a protractor, for one thing. Neither are spirals, helixes, all five corners of a pentagon, or points on a globe.

Here are some examples of non-collinear points:

Non-collinear points are a set of points that do not lie on the same line. Picture a sushi roll in front of you. Sticking with our example above, a second skewer of food sitting next to ours would not have any points collinear with our skewer, since they are all on a different skewer or line.

Points must lie on the same line to have collinearity. If picture a right triangle with two points label on two different sides points L and R. If point L on the hypotenuse and point R on the base, then point L and point R are non-collinear.

Collinear Points in Geometry

Very often, collinear points appear in geometric figures such as quadrilaterals, triangles, parallelograms, and more. Take this kite with two diagonals intersecting at $Point S$:

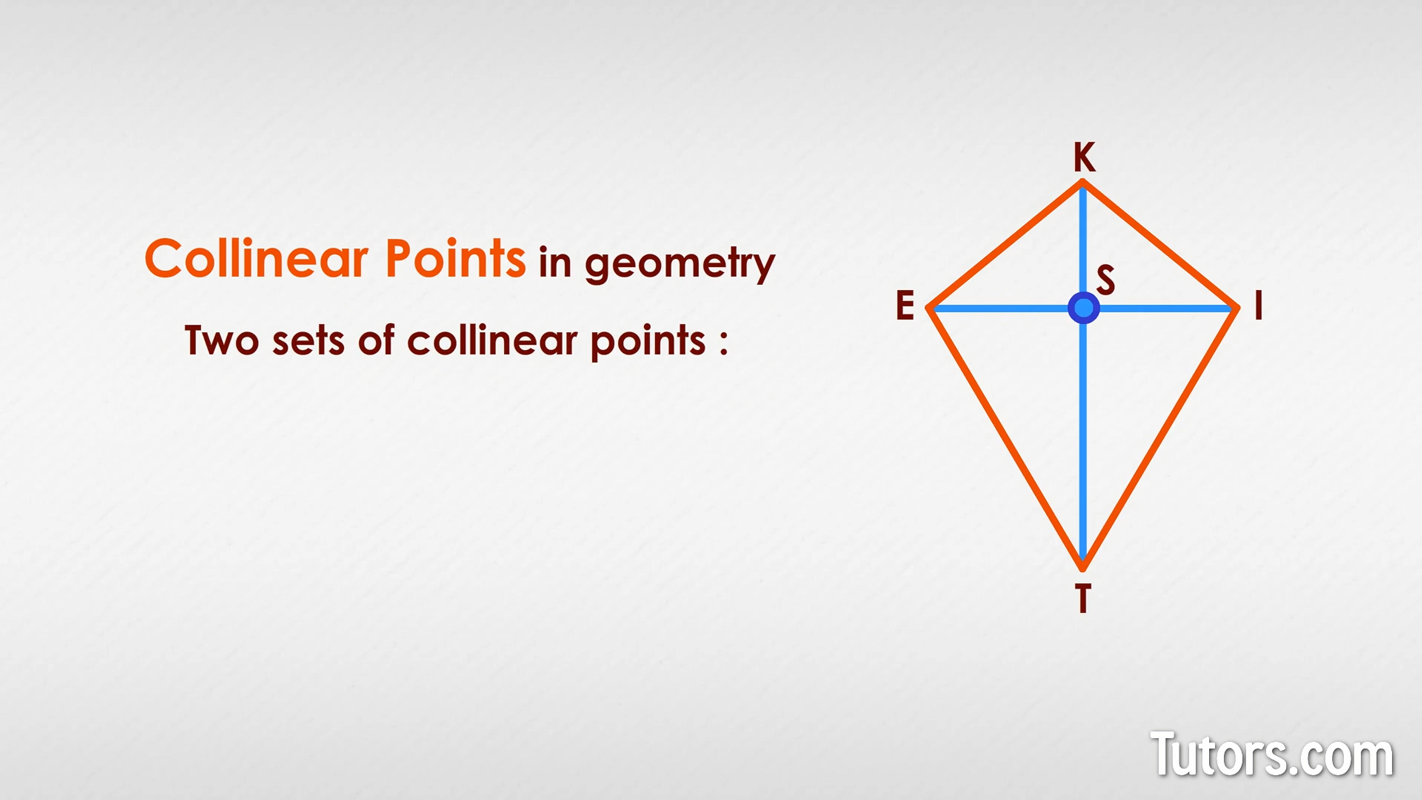
Two sets of collinear points appear around the diagonals in this geometric figure:

1. $K-S-T$
2. $I-S-E$

But you can also find all these other collinear points since only two points determine a line:

• $KS$
• $ST$
• $IS$
• $SE$
• $KI$
• $IT$
• $TE$
• $EK$

Collinear Points Examples

We will leave you with a side view of a little street brazier for making skewered meat kebabs. Notice the legs cross and have a bottom brace, which creates two triangles to keep the brazier stable. Can you find at least $10$ sets of collinear points?

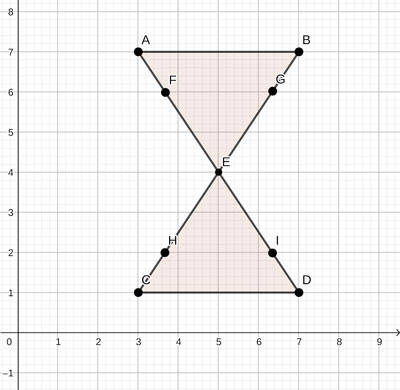
We are sure you saw sets like points $A$ and $B$, $C$ and $D$, and points $A - F - E - I - D$, but did you also pick up on ones like $CH, HE, EG,$ and $GB$?

The points $C - H - E$ and $E - I - D$, which form two sides of a triangle (the bottom triangle) are also collinear.

Look at points $H - E - G$ and $E - G - B$. Each of these three points are collinear as well. Keep looking; more sets of collinear points are waiting to be found!

Coplanar Points

We now know that collinear points, sometimes spelled "colinear" (just on L), are points that lie on a straight line. But what about coplanar points? In a three dimensional world, coplanar points are a set of points that lie on the same plane. Learn more about coplanar points.

Next Lesson:

Geometric Constructions