What are Horizontal Lines? — Slope, Equations, & Examples
What is a horizontal line?
For a line to be horizontal, it must mimic the flat, broad, straight line that earth's horizon shows. A horizontal line is a line that neither rises nor falls; it has no slope at all.
Humans' earliest experience with horizontal lines gave the lines their name: earth's horizon appears flat and straight because we are so small and the earth is so big.
Our word "horizon" began as a Greek word meaning "limiting," as in a boundary. Earth's horizon is a limit; you can see to the horizon, but not beyond. The Greeks would have seen earth's apparent horizon as they gazed out over the Ionian Sea, the Aegean Sea, and the Sea of Crete.
Indoor horizons?
Horizontal lines are all around you, because humans have learned to make right angles for our walls, floors and ceilings. The intersection of the two planes of your room's flat ceiling and straight wall is a horizontal line. The intersection of your room's floor plane and wall plane is also a horizontal line.
Windows show horizontal lines. Look through a handy window, noticing its horizontal lines at the top and bottom. Outside you can see horizontal siding on houses. Roof lines of buildings and homes show many horizontal lines.
Graph a horizontal line
If you take a piece of graph paper and construct an x-axis and y-axis, a horizontal line will stretch from the left side of the paper to the right with the same y-value throughout:
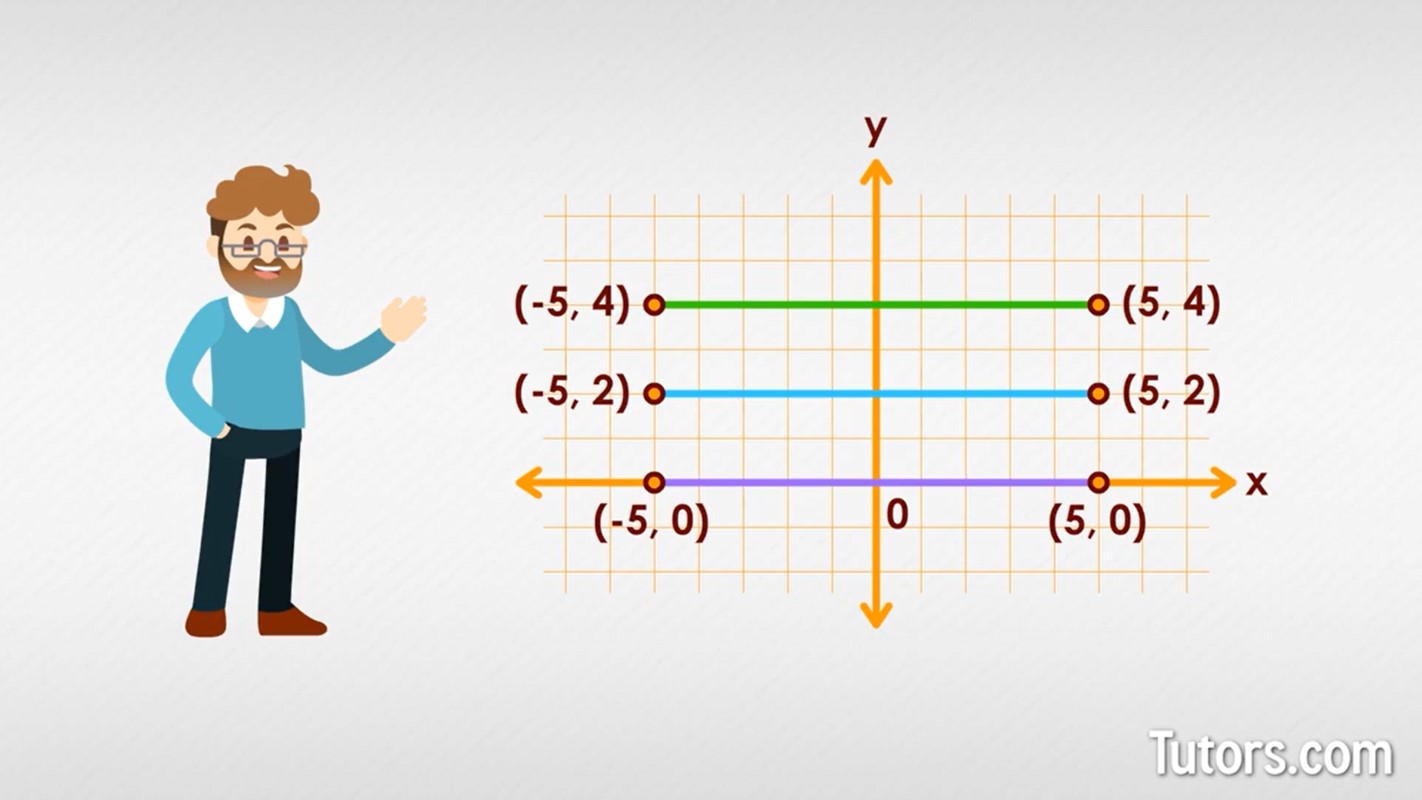
If you add another horizontal line, you will have to make it parallel to your first one, either at a greater or lesser y value. Suppose you made your first horizontal line starting in Quadrant II, at (−5, 4), and stretching into Quadrant 1 at (5, 4).
Your next horizontal line could be at (−5, 2) and go across to (5, 2). You could even have a horizontal line at (−5, 0) slicing right through the origin (0, 0) to end at (5, 0) on the x-axis.
Dance dance horizon
Unless you are particularly vigorous and athletic, most of your dance moves on the dance floor will move you along horizontal lines, not vertical lines. Say you start out near the snack table, (x, y) = (0, 1), and slip slide 10 paces over to the DJ to request a tune.
You moved across the floor, but you did not go upstairs or into the basement. You may have moved 10 paces to your right (x = 10), but your y value is still 1: (10, 1).
You spot a great dance partner, and step in style over to your partner to dance together. Maybe your partner is 5 paces further to your right, so your x = 15 but your y value is still 1; you did not climb stairs or take an elevator down: (15, 1).
Your line of movement is always horizontal; you did not rise or fall below the level of the dance floor.
Now say you have a reason to climb the stairs to the second floor; perhaps the first floor bathroom is out of order. Now you have changed your y-value, and your movements across the second floor are all y = 2.
Slope of a horizontal line
The slope of a line is its steepness, or its rise (up and down) over its run (left to right). Another way to consider slope is as a:
Most mathematicians let m = the slope of a line. So a rising line from left to right has a positive slope, a falling line has a negative slope, and a horizontal line has a slope of 0.
Go back to your second-story search for that working bathroom (too many trips to the punch bowl?). You moved around a lot, but always at y = 2.
Say you walked 20 paces from left to right, so your change in x-value is 20. But look at your change in y-value: you stayed on the second floor the whole time. Your slope is:
What is 0 divided by 20? It's 0! The line of your movement has no slope; the slope is 0.
The numerator of every slope calculation with a horizontal line will be 0. The slope will always be 0.
Horizontal line equation
We started off on the first floor of the dance, so our original point, (x1, y1) was (0, 1). Recall we moved 15 paces across the floor, but stayed on the first floor, ending at (15, 1), which is our ending point, (x2, y2).
We can use those ordered pairs to calculate m:
Our change in x is 15, and our change in y is 0, so our slope is 0.
Slope intercept formula
You may recall that the slope intercept formula for any line is
The m is the slope of the line, and b is the y-intercept (the value of y where it crosses the x-axis). If you already know that the slope (m) of any horizontal line is 0, then the formula simplifies to
Can you see the reason this is true? With a slope of 0, any x-value disappears! The y-intercept is the y-value.
Lesson summary
Now that you have worked and danced your way through this lesson, you are able to recall and apply a definition of horizontal lines, cite examples of horizontal lines, link horizontal lines in your world with horizontal lines in coordinate graphing, and identify the slope of any horizontal line as 0.