Volume of a Cube — Formula, How To Find & Examples
Volume of a cube
The volume of a cube is how much space the cube takes up in three-dimensions. The volume of a cube is always measured in cubic units derived from the linear unit given or used to measure the side length.
You can find the volume of any cube with one given measurement using the volume of a cube formula:
What is a cube?
A cube is a three-dimensional solid with six congruent square faces meeting at right angles, eight vertices, and twelve equal length sides. A cube is one of the five Platonic Solids and is also called a hexahedron.
What are the dimensions of a cube?
A cube is a 3D object, so a cube has three dimensions:
Length – Generally understood to be the larger of the “flat” dimensions.
Width – Generally understood to be the shorter of the “flat” dimensions.
Height or Depth – The dimension that brings the shape into our 3D world
Notice, we have two ways to describe the third dimension:
Height – Use this term when the object rises before you, like a tall building.
Depth – Use this term if the object drops beneath you, like a hole in the ground.

We need information about at least one of these three dimensions to measure the volume of a cube.
Volume of a cube formula
The volume formula is volume equals length times width times height.
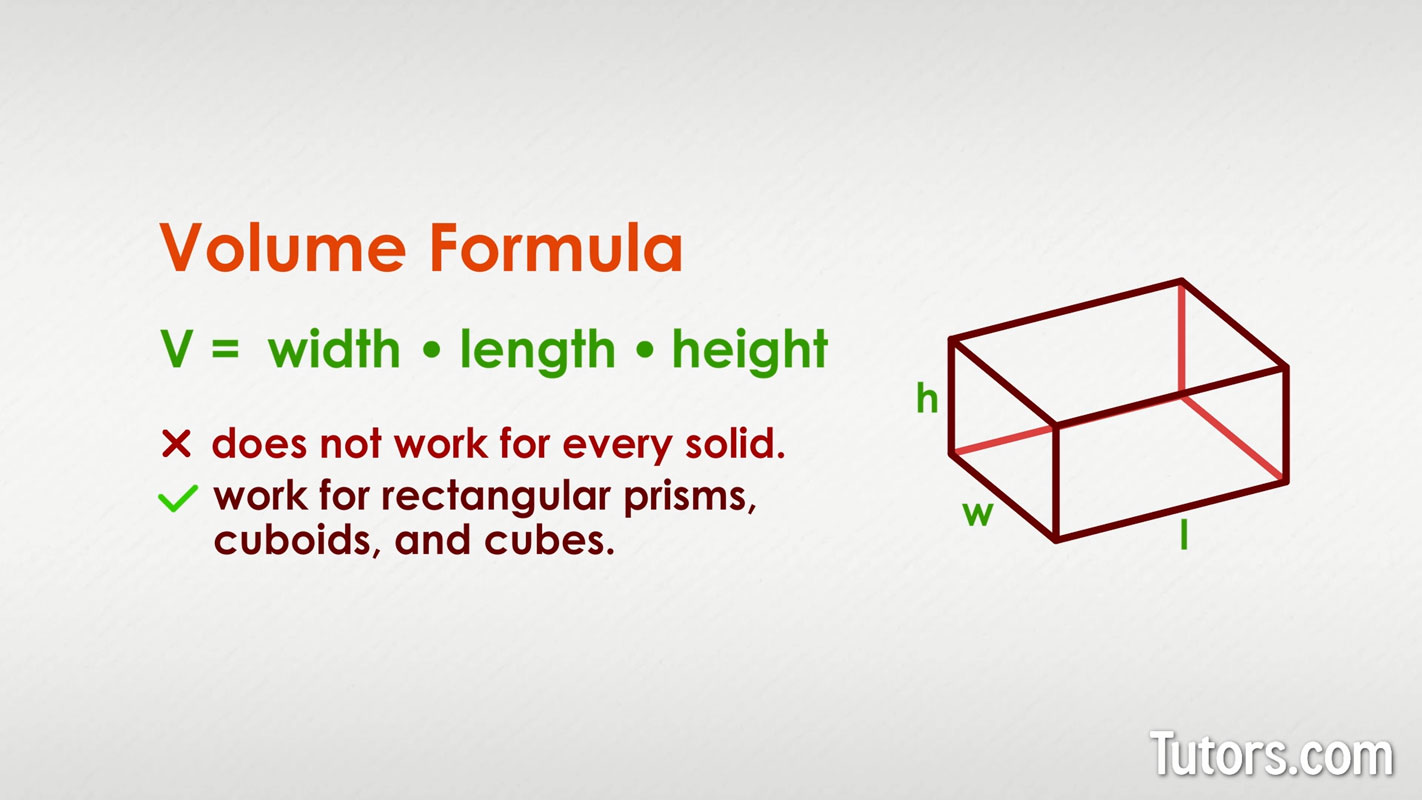
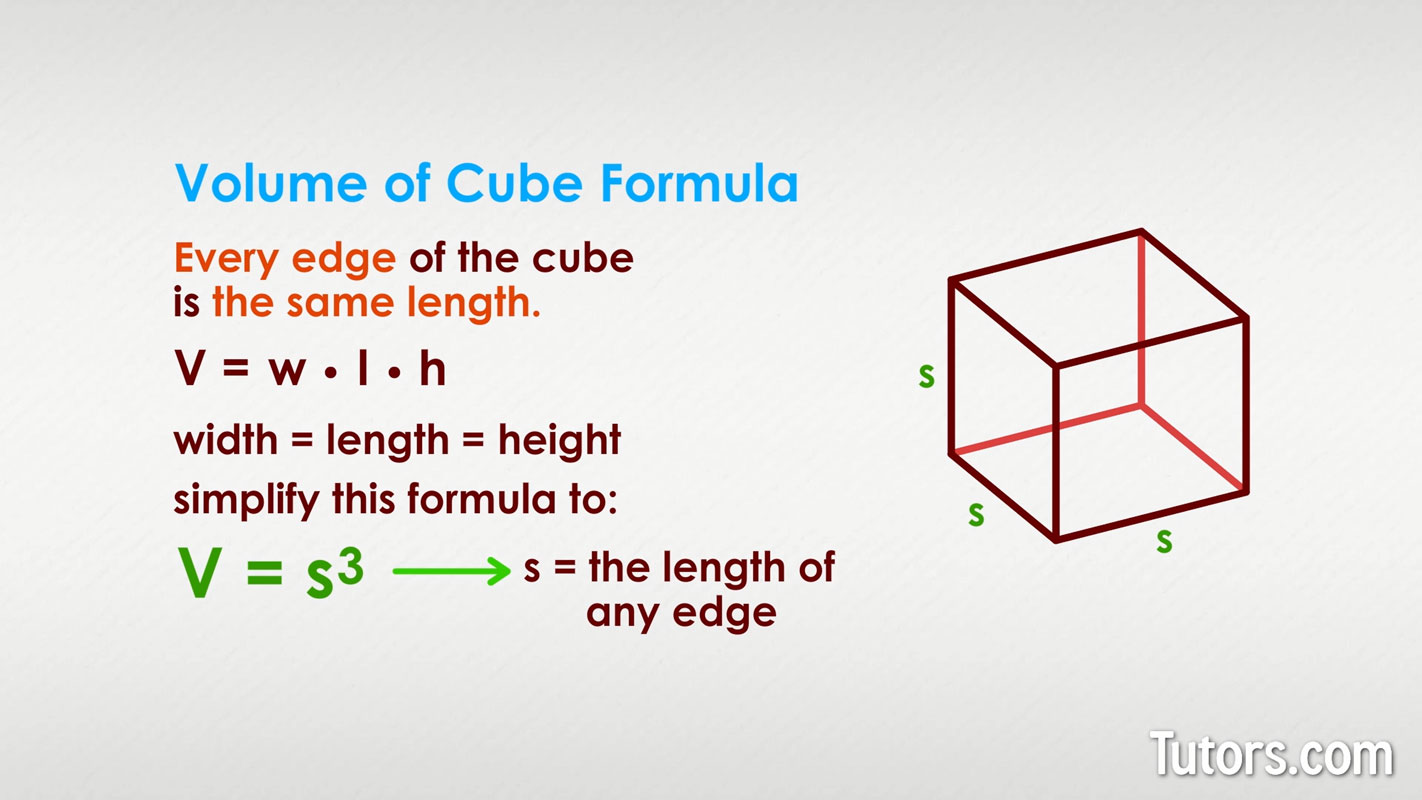
Because all three values (l, w, and h) are the same in a cube, the simplest volume of a cube formula is:
In this volume of a cube equation, s = the length of any edge.
Volume is always measured in cubic units based on the linear units provided to you. If you are told the edge of the cube measures 3 meters, the volume is measured in cubic meters or (meters cubed).
How to find volume of a cube
To find the volume of a cube, you only need to know the length of any edge.
If you are given one side length, you can find the volume of a cube by plugging it into either one of the volume formulas for a cube:
Measuring the space a cube takes up is a matter of knowing the length of any one edge because all the side lengths of a cube are equal in length.
How to find length, width, and height from volume
What if you are given the volume of a cube and asked to find the cube's dimensions?
If you are given the volume of the cube and asked to find the length of an edge, all you have to do is take the cube root of the volume:
Your answer will no longer be in cubic units; it will be in linear units.

What if we have a cube, and we are told its volume is 729 cubic meters. To find the length of an edge of the cube:
How to calculate volume using area
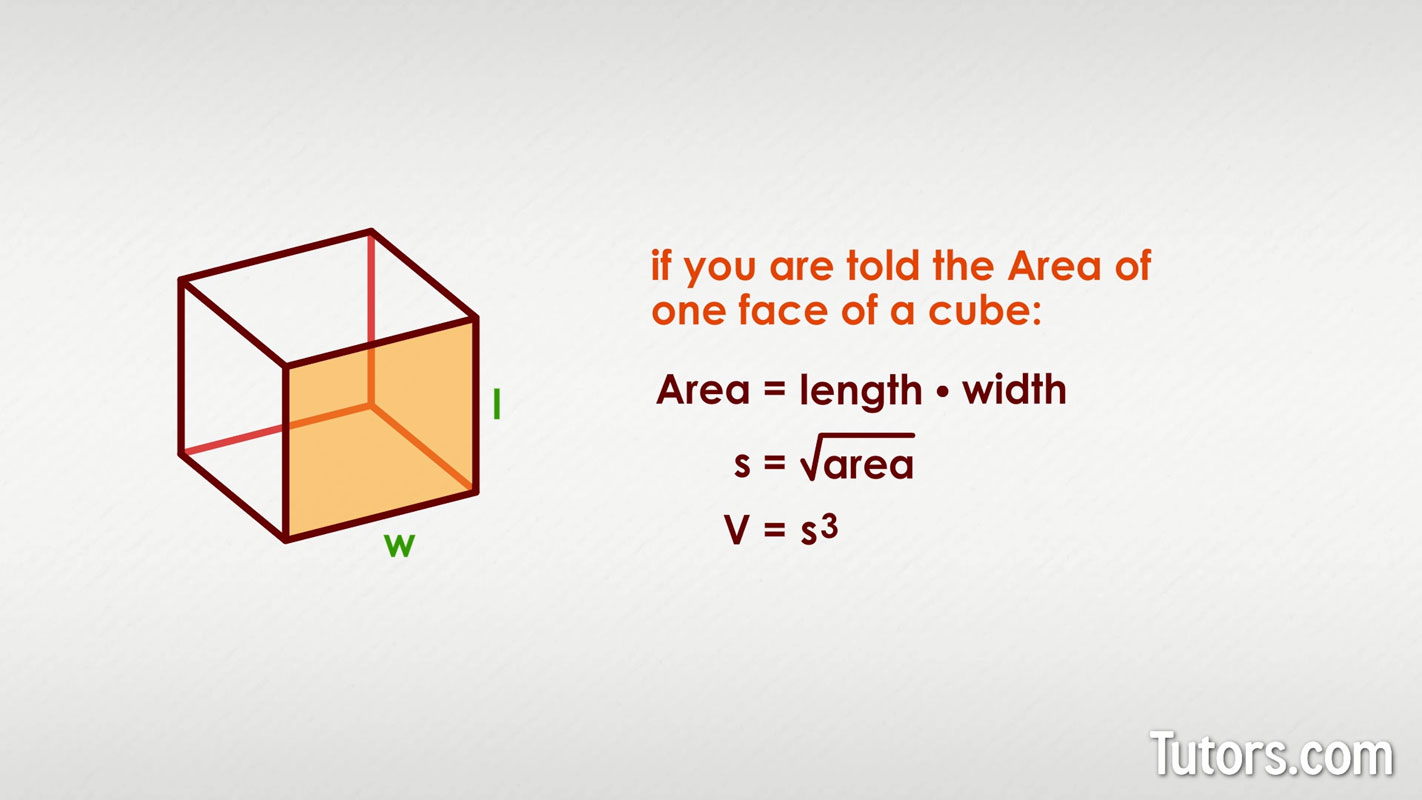
Here's another challenge. What if you are told the area of one face of a cube? Can you use that information to find the volume?
Yes, the area of one face is the face's length times width. Once you find the width or length, you can apply the volume formula:
Find the square root of the given area measurement; this will give you the length of any side, s.
Use the volume formula, , to find the area.
How to calculate surface area of a cube using volume
If you are given the volume of a cube, you can convert that into the length of one side. Then, you can use the side length to calculate the total surface area.
Use the edge length to calculate the surface area of one side, then multiply that area by 6. This gives you the total surface area of a cube using volume.
What if you are told the total surface area of the entire cube? Can you find the volume?
Yes, the total surface area combines the area of all six, congruent faces. Find the area of one face, and then use the steps outlined above to find the volume:
Divide the given total surface area by six, to get the area of one face
Find the square root of the area of one face to get the length of any side, s.
Use the volume formula,

Volume of a cube examples
If you have a three-dimensional solid with six faces, and the sides are labeled 4', 6', and 8'. Is it a cube? No, this is a rectangular prism because the labels that outrank the drawing, show different lengths!
What if the sides of our solid were 4', 4', and 4'; Is this a cube? Yes, this is a cube because the labels tell you the width, length, and height are all the same.
What is the volume of the cube above?
Did you write down ?
Did you calculate ?
Let's look at another example of a cube with a side length of 12 yards. What is its volume?
What about a cube that has one face with an area of 25 cm. What is the volume of the cube?
First, what is the length of any edge or side of the cube?
Think: what is the square root of 25? The answer is 5, so:
Now that you have the length of the side, you can calculate the volume:
Now, let's try to find the volume given the surface area. The total surface area of a cube is 7,776 square inches. What is the volume of the cube? Remember, the total surface area is the area of all six square faces. Divide the total surface area by 6, take the square root of that, then use the volume formula:
Now we can calculate the volume of the cube: