What Is A Mixed Number? — Definition & Examples

Written by

Malcolm McKinsey

January 12, 2023

Fact-checked by

Paul Mazzola

Mixed numbers

A mixed number is a whole number and a proper fraction. Mixed numbers or mixed fractions are used to express an amount greater than a whole but less than the next whole number. Mixed numbers can be formed from improper fractions. They're useful in describing units that cannot be equally divided.

Fractions and mixed numbers

Fractions by themselves are often easy to understand. Whole numbers are easy. When fractions and whole numbers get together, though, the mixed numbers can be much more challenging to understand.

You are probably familiar with fractions, which are usually parts of a whole and always existing (in proper form) between the whole numbers 0 and 1:

• $\frac{1}{2}$

• $\frac{3}{4}$

• $\frac{7}{8}$

• $\frac{1}{16}$

• $\frac{25}{32}$

Improper fractions can be whole numbers in disguise:

• $\frac{4}{2}=2$

• $\frac{9}{3}=3$

• $\frac{100}{10}=10$

Or improper fractions can be mixed numbers awaiting simplification:

• $\frac{4}{3}=1\frac{1}{3}$

• $\frac{7}{3}=2\frac{1}{3}$

• $\frac{105}{10}=10\frac{1}{2}$

After simplifying these improper fractions, you are left with a whole number plus a remainder, which is the additional fraction.

The combination of a whole number and a proper fraction is called a mixed number.

Mixed numbers examples

Suppose you have a set of baseball trading cards for your favorite team. It is 17 cards. One card is $\frac{1}{17}$, a fraction of the whole set. The entire collection is $\frac{17}{17}$, or 1 whole.

What if a friend gives you a handful of additional trading cards?

You count the new cards – your friend gave you 5 cards. You now have more than one whole set, but you do not have a complete second set of 17 cards, so you have a mixed number.

So, how many sets of baseball cards do you have?

• Original set: $\frac{17}{17}$ or 1 whole set

• New cards: 5

• Total sets: 1 and $\frac{5}{17}$or $1\frac{15}{17}$

You have 1 and five−seventeenths ($\frac{5}{17}$) sets of baseball trading cards.

Mixed numbers can be used to describe everything from batches of baked cookies to timings of movies to any unit or set that can be divided into parts.

How to solve mixed fractions

Pizza, cookies, cupcakes, and many other foods lend themselves to breaking up into whole units and fractions, which means they can also form mixed numbers.

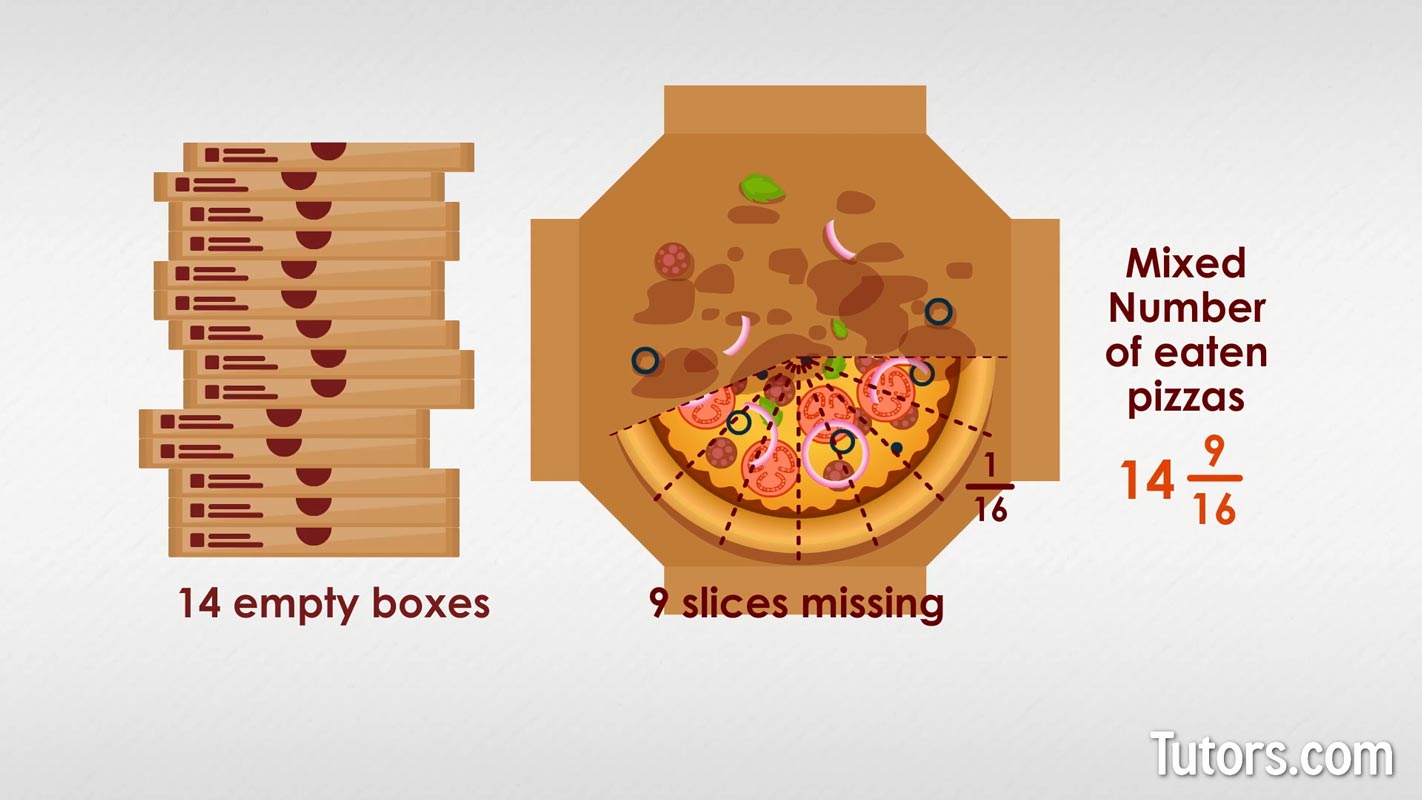
Your math club orders pizzas cut into 1/16th slices for your Math Night. You ordered 15 pizzas, but not every pizza was consumed.

That means the adoring crowd of math lovers ate 14 whole pizzas and 9 slices, each 1/16th.

That makes the mixed number $14\frac{9}{16}$

Convert improper fraction to mixed number

Earlier, we mentioned that improper fractions were disguising whole numbers or mixed numbers in them. They are improper because their numerators are not smaller than their denominators:

• $\frac{11}{8}$

• $\frac{5}{2}$

• $\frac{14}{7}$

• $\frac{64}{24}$

To convert an improper fraction to its mixed number form, we divide the numerator (top number) by the denominator (bottom number).

The whole number you get is the whole number part of a mixed number, and the remainder is the numerator of the fraction part of the mixed number.

The denominator of your mixed number is the same denominator as your improper fraction.

Let's look at an example:

Here is another one:

Our third example:

In the last example, notice that we reduced the fractional part down to its simplest form.

Mixed numbers to fractions

Mixed numbers become improper fractions easily by multiplying the whole number times the fraction's denominator and adding the numerator. It is a counterclockwise process.

Here is $5\frac{6}{7}$ being converted to an improper fraction:

• $5\times 7=35$

• $35+6=41$

• $5\frac{6}{7}=\frac{41}{7}$

Mixed number practice problems

Here are five word problems for you to solve:

1. In the mixed number $3\frac{7}{10}$, what is the whole number, and what is the fraction?

2. Is $\frac{27}{9}$ a proper fraction, improper fraction, mixed number, or whole number? Can it simplify to another form?

3. Change $\frac{13}{8}$ to a mixed number.

4. What is $\frac{56}{50}$ as a mixed number?

5. Change the mixed number $3\frac{7}{8}$ to an improper fraction.

Take a fraction of a second to think about each before you peek!

1. The whole number is 3, and $\frac{7}{10}$ is the fraction.

2. $\frac{27}{9}$ is an improper fraction. It can be simplified to the whole number 3.

3. To change $\frac{13}{8}$ to a mixed number, divide 13 by 8 and use the remainder as the new numerator: $1\frac{5}{8}$

4. $\frac{56}{50}$ is $1\frac{3}{25}$ as a mixed number.

5. The mixed number $3\frac{7}{8}$ becomes the improper fraction $\frac{31}{8}$.