Division Property Of Equality — Definition & Example

Written by

Malcolm McKinsey

January 11, 2023

Fact-checked by

Paul Mazzola

Division property of equality definition

The division property of equality says that dividing both sides of an equation by the same number does not affect the equation. Another way to consider it is that if you divide one side of an equation by a number, you must divide the other side by the same number.

Division property of equality formula

The division property of equality states:

If $a=b$ , then $\frac{a}{c}=\frac{b}{c}$ This is very similar to the multiplication property of equality, in which we can multiply both sides of any equation without affecting the equation.

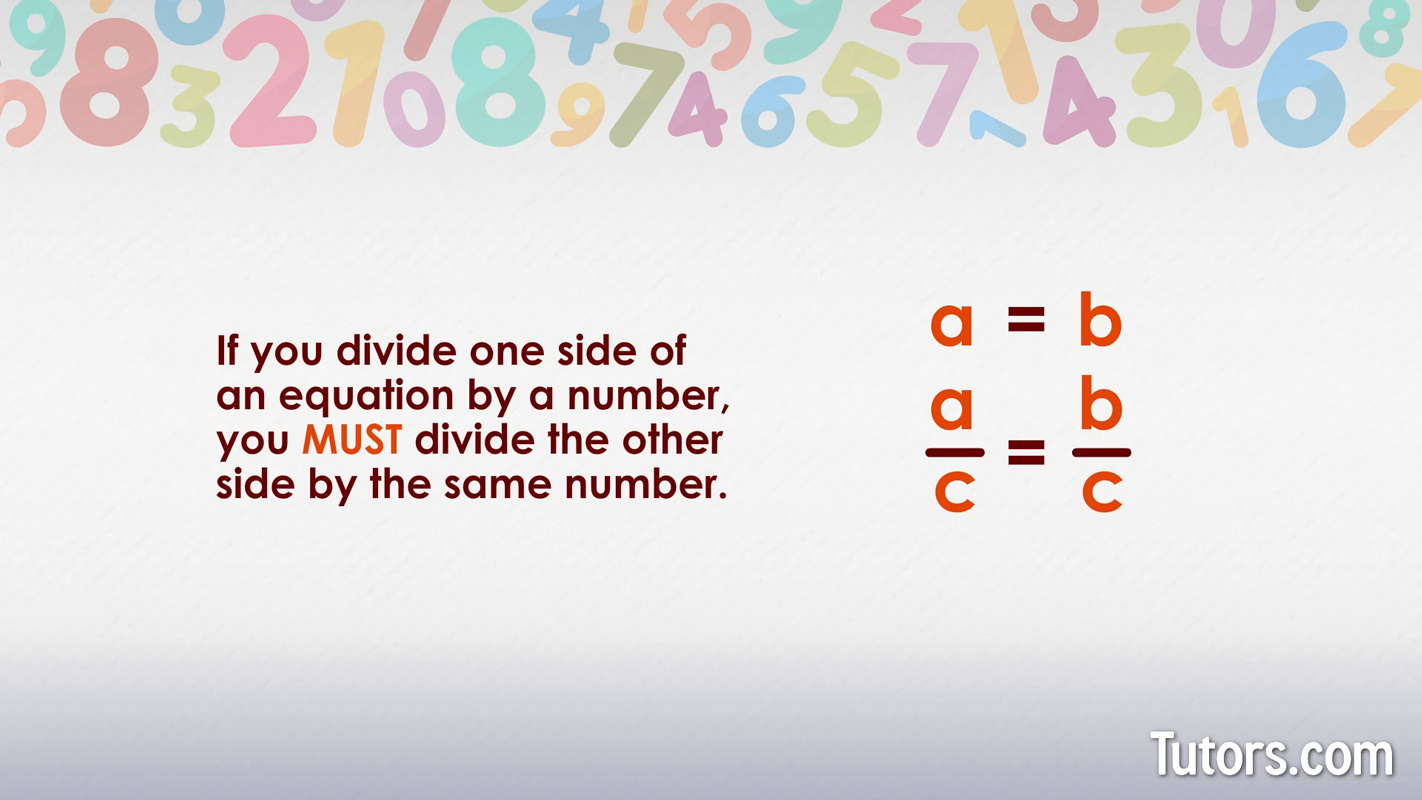
The properties of equality are:

Division property of equality
Subtraction property of equality
Addition property of equality
Multiplication property of equality

Get free estimates from math tutors near you.

Division property of equality example

Division is a method of sharing fairly. In equations, you need to operate on both sides of the equals sign fairly. Whatever you do to the left side of the equal sign, you must do it to the right side of the equation as well.

Division property of equality definition

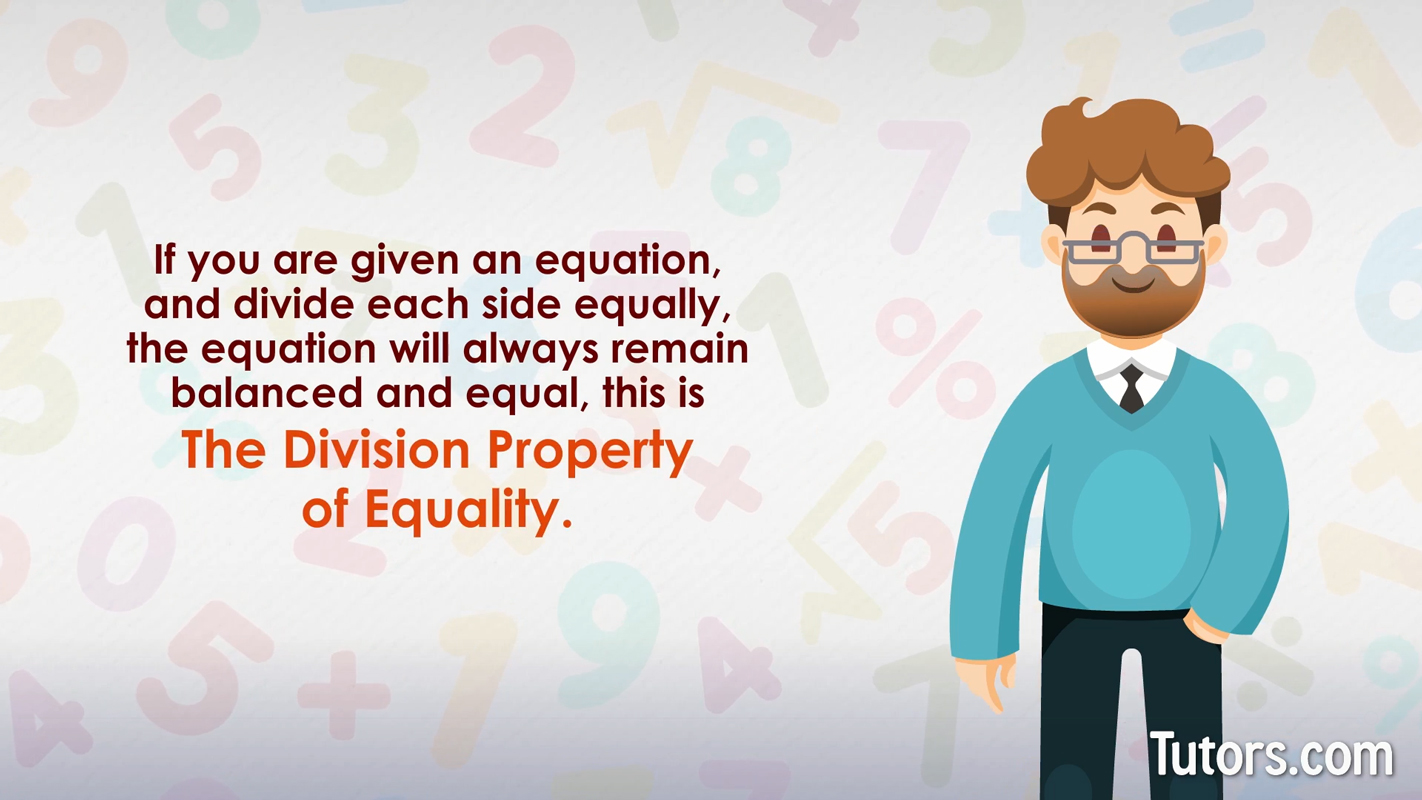
You cannot take away or divide something from one side without doing the same thing to the other side.

Suppose you are sharing 2 pans of donated brownies among all the members of your Math Club.

You need to serve from both pans equally, so the 2 donors will not have their feelings hurt. You dish out 2 brownies from the first pan, so you dish out 2 brownies from the second pan, too.

Division is really just fast, repeated subtraction, so instead of just dishing out 2 brownies from each pan, we can cut both pans into 12 brownies and divide them into piles of 2:

We had 12 brownies on both sides, each divided by 2. Both sides of our brownie equation show 6 piles of 2 brownies in each pile.

The division property of equality works with all real numbers and with algebraic expressions using variables.

Here are examples using integers:

-24=-12\times 2

\frac{-24}{6}=\frac{\left(-12\times 2\right)}{6}

-4=-4

Here is an example with fractions:

\frac{3}{4}=\frac{6}{8}

\frac{3}{4}\div \frac{1}{4}=\frac{6}{8}\div \frac{1}{4}

3=3

Here is an example using mixed numbers:

2\frac{1}{4}=\frac{10}{4}

2\frac{1}{4}\div \frac{3}{8}=\frac{10}{4}\div \frac{3}{8}

6\frac{2}{3}=6\frac{2}{3}

Here is an example using decimals:

0.6500=0.65

\frac{0.6500}{325}=\frac{0.65}{325}

0.002=0.002

Here is an example using variables:

8x=40

\frac{8x}{8}=\frac{40}{8}

x=5